а)Для всякой матрицы порядка n имеет место формула разложения определителя ее по первому столбцу:
det A= 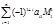
б) Определитель транспонированной матрицы (квадратной) равен определителю исходной матрицы, т.е.
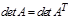 .
.
в) При перестановке местами двух строк или двух столбцов матрицы определитель ее сохраняет абсолютную величину, но меняет знак на противоположный.
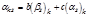 ; k= 1,2,¼, n; b,c Î R,
то
; k= 1,2,¼, n; b,c Î R,
то 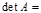
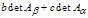 ,
где
,
где 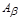 и
и 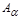 - матрицы полученные из А заменой s- ого столбца ее на столбцы (a) и (b) соответственно.
д) Определитель матрицы A равен нулю, если:
1. Матрица A имеет одинаковые строки или столбцы;
2. Строка (столбец) матрицы A является линейной комбинацией других строк (столбцов);
3. Матрица A имеет нулевую строку или столбец.
е) Сумма произведений элементов какой-либо строки (столбца) матрицы на их алгебраические дополнения равна определителю этой матрицы.
ё)Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.
ж) Определитель произведения квадратных матриц равен произведению определителей этих матриц.
з)если строку\столбец матрицы умножить на число, то ее определитель увеличится на это число.
и)если сложить поэлементно 2 строки\столбца, одну из них домножив на число, то определитель не изменится.
к)определитель матрицы треугольного вида = произведению её главной диагонали
- матрицы полученные из А заменой s- ого столбца ее на столбцы (a) и (b) соответственно.
д) Определитель матрицы A равен нулю, если:
1. Матрица A имеет одинаковые строки или столбцы;
2. Строка (столбец) матрицы A является линейной комбинацией других строк (столбцов);
3. Матрица A имеет нулевую строку или столбец.
е) Сумма произведений элементов какой-либо строки (столбца) матрицы на их алгебраические дополнения равна определителю этой матрицы.
ё)Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.
ж) Определитель произведения квадратных матриц равен произведению определителей этих матриц.
з)если строку\столбец матрицы умножить на число, то ее определитель увеличится на это число.
и)если сложить поэлементно 2 строки\столбца, одну из них домножив на число, то определитель не изменится.
к)определитель матрицы треугольного вида = произведению её главной диагонали
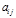 и определителем отличным от нуля. Такие матрицы в дальнейшем будем называть невырожденными.
Квадратные невырожденные матрицы А и В порядка n называются взаимно обратными, если их произведение коммутативно и равно единичной матрице, т.е. АВ=ВА=Е. Обратная матрица к матрице А обозначается символом
и определителем отличным от нуля. Такие матрицы в дальнейшем будем называть невырожденными.
Квадратные невырожденные матрицы А и В порядка n называются взаимно обратными, если их произведение коммутативно и равно единичной матрице, т.е. АВ=ВА=Е. Обратная матрица к матрице А обозначается символом 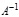 и удовлетворяет условию А
и удовлетворяет условию А 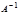 =
= 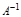 А=Е.
Существование обратной матрицы
Теорема. Для того чтобы матрица А имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля, т.е. матрица А невырожденная.
НА КЛЕЧ.ЛИСТКЕ.
А=Е.
Существование обратной матрицы
Теорема. Для того чтобы матрица А имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля, т.е. матрица А невырожденная.
НА КЛЕЧ.ЛИСТКЕ.
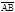 будем называть направленный отрезок, имеющий начало в точке А и конец в точке В. Вектор часто обозначают одной буквой, например,
будем называть направленный отрезок, имеющий начало в точке А и конец в точке В. Вектор часто обозначают одной буквой, например, 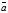 .
Модулем или длиной вектора
.
Модулем или длиной вектора  =
= 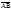 называют длину отрезка АВ и обозначают символом |
называют длину отрезка АВ и обозначают символом | 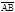 | º |
| º | 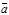 | º а.
Вектор, начало и конец которого совпадают, т.е.
| º а.
Вектор, начало и конец которого совпадают, т.е. 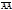 , будем называть нуль-вектором и обозначать символом
, будем называть нуль-вектором и обозначать символом 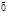 . Направление нуль-вектора можно выбирать произвольно.
Два вектора
. Направление нуль-вектора можно выбирать произвольно.
Два вектора  и
и  называются равными, если:
a. Длины векторов равны, т.е. |
называются равными, если:
a. Длины векторов равны, т.е. | 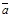 | = |
| = | 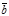 |;
b. Векторы
|;
b. Векторы 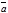 и
и 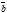 параллельны, т.е. расположены на параллельных или совпавших прямых;
c. Векторы
параллельны, т.е. расположены на параллельных или совпавших прямых;
c. Векторы 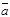 и
и 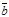 одинаково направлены (рис. 7).
одинаково направлены (рис. 7).
 Рис.7
Рис.7
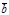 l
В дальнейшем условимся не различать равные векторы, т.е. множество равных векторов будем понимать как один вектор, имеющий начало в произвольной точке, так называемый свободный вектор.
2.Сложение векторов.
Суммой векторов
l
В дальнейшем условимся не различать равные векторы, т.е. множество равных векторов будем понимать как один вектор, имеющий начало в произвольной точке, так называемый свободный вектор.
2.Сложение векторов.
Суммой векторов 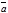 ,
, 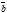 ,
, 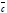 будем называть вектор
будем называть вектор 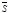 , начало которого совпадает с началом первого вектора, а конец совпадает с концом последнего вектора, при условии что начало последующего вектора совпадает с концом предыдущего (рис. 8)
, начало которого совпадает с началом первого вектора, а конец совпадает с концом последнего вектора, при условии что начало последующего вектора совпадает с концом предыдущего (рис. 8)
 Замечание. Для сложения двух векторов можно воспользоваться «правилом параллелограмма»: суммой двух векторов
Замечание. Для сложения двух векторов можно воспользоваться «правилом параллелограмма»: суммой двух векторов 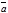 и
и 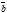 называется третий вектор
называется третий вектор 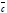 , имеющий общее начало с векторами
, имеющий общее начало с векторами  и
и  и совпадающий с диагональю параллелограмма, построенного на этих векторах (рис. 9).
и совпадающий с диагональю параллелограмма, построенного на этих векторах (рис. 9).
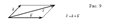 Операция сложения векторов обладает свойствами:
1.
Операция сложения векторов обладает свойствами:
1.  +
+  =
=  +
+  ;
2.
;
2.  +(
+( +
+ 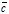 )=(
)=( +
+  )+
)+ 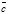 3.
3.  +
+ 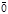 =
=  ;
4. Вектор -
;
4. Вектор -  называется противоположным вектору
называется противоположным вектору  ; вектор -
; вектор -  имеет длину равную длине вектора
имеет длину равную длине вектора  , но противоположное направление, т.е.
, но противоположное направление, т.е. 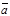 +(-
+(- 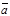 )=
)= 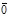 .
3.Вычитание векторов.
Разностью двух векторов
.
3.Вычитание векторов.
Разностью двух векторов 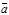 и
и 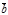 будем называть сумму векторов
будем называть сумму векторов 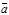 и -
и - 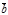 , т.е.
, т.е. 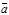 +(-
+(- 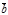 ) (рис. 10).
) (рис. 10).
 4.Умножение вектора на число.
Произведением вектора
4.Умножение вектора на число.
Произведением вектора 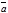 на число l называется вектор
на число l называется вектор 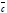 длины
|
длины
| 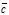 | = | l |× а, направление которого совпадает с направлением
| = | l |× а, направление которого совпадает с направлением 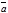 , если l > 0, противоположно
, если l > 0, противоположно  , если l < 0. При l=0
, если l < 0. При l=0 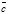 =0.
Операция умножения вектора на число обладает свойствами:
(a+b)
=0.
Операция умножения вектора на число обладает свойствами:
(a+b)  =a
=a  +b
+b  , a,bÎR;
a(
, a,bÎR;
a( +
+  )=a
)=a  +a
+a  ;
a(b
;
a(b 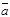 )=(ab)
)=(ab) 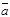 ;
1´
;
1´  =
=  , (-1)´
, (-1)´  =-
=-  , 0´
, 0´  =
= 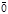 .
Замечание. Вектор
.
Замечание. Вектор 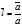 называется единичным вектором или ортом направления, определяемого вектором
называется единичным вектором или ортом направления, определяемого вектором 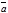 . Очевидно имеет место равенство
. Очевидно имеет место равенство 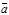 = а
= а 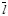 .
5.Коллинеарные векторы.
Два вектора
.
5.Коллинеарные векторы.
Два вектора 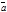 и
и 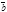 называются коллинеарными, если они расположены на одной прямой или на параллельных прямых.
Заметим, что нулевой вектор коллинеарен любому вектору.
Теорема 1. Для того чтобы два вектора
называются коллинеарными, если они расположены на одной прямой или на параллельных прямых.
Заметим, что нулевой вектор коллинеарен любому вектору.
Теорема 1. Для того чтобы два вектора  и
и  были коллинеарны необходимо и достаточно, чтобы они были пропорциональны, т.е. имело место равенство
были коллинеарны необходимо и достаточно, чтобы они были пропорциональны, т.е. имело место равенство 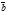 =l
=l 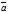 , lÎ R.
6.Компланарные векторы.
Три или более векторов называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Теорема 2. Для того чтобы три вектора
, lÎ R.
6.Компланарные векторы.
Три или более векторов называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Теорема 2. Для того чтобы три вектора 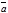 ,
, 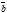 ,
, 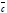 были компланарными необходимо и достаточно, чтобы один из них был линейной комбинацией двух других, т.е.
были компланарными необходимо и достаточно, чтобы один из них был линейной комбинацией двух других, т.е. 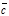 =a
=a 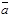 +b
+b 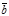 , a,bÎ R.
Доказательство.
Необходимость. Пусть векторы
, a,bÎ R.
Доказательство.
Необходимость. Пусть векторы 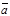 ,
, 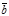 ,
, 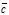 компланарны, расположены в одной плоскости и имеют общее начало О (этого можно достичь параллельным переносом).
Предположим сначала, что среди этих векторов существуют два неколлинеарных вектора, например
компланарны, расположены в одной плоскости и имеют общее начало О (этого можно достичь параллельным переносом).
Предположим сначала, что среди этих векторов существуют два неколлинеарных вектора, например  и
и  . Тогда представляя вектор
. Тогда представляя вектор 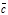 в виде суммы векторов
в виде суммы векторов 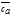 и
и 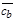 , соответственно коллинеарных
, соответственно коллинеарных 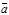 и
и 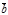 , будем иметь
, будем иметь
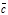 =
= 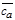 +
+ 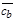 (рис. 11)
(рис. 11)
 Так как векторы
Так как векторы 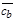 и
и 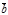 ,
, 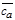 и
и 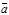 попарно коллинеарны, то
попарно коллинеарны, то 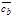 =b
=b 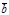
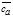 =a
=a 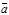 и
и 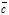 =a
=a 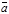 +b
+b 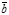 . Если все три вектора коллинеарны, то вектор
. Если все три вектора коллинеарны, то вектор 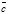 можно представить в виде
можно представить в виде 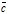 =a
=a 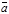 +0
+0 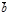 Достаточность. Пусть векторы
Достаточность. Пусть векторы 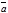 ,
, 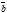 ,
, 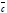 удовлетворяют условию
удовлетворяют условию 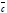 =a
=a 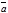 +b
+b 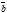 . В этом случае вектор
. В этом случае вектор 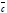 лежит в той же плоскости, что и векторы
лежит в той же плоскости, что и векторы 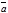 и
и 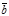 , в силу определенных операций: сложения векторов и умножения вектора на число.
Теорема доказана.
, в силу определенных операций: сложения векторов и умножения вектора на число.
Теорема доказана.
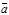 на ось Z наз. число
на ось Z наз. число 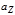 =
= 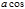 j, где j - угол между вектором
j, где j - угол между вектором 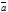 и направлением оси Z.
Если
и направлением оси Z.
Если 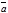 =
= 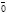 , то проекция его на любую ось равна нулю.
Проекция вектора
, то проекция его на любую ось равна нулю.
Проекция вектора 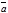 на ось Z обозначается символом
на ось Z обозначается символом 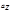 =
= 
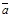 (рис. 12).
(рис. 12).
 Вектор
Вектор 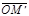 называется составляющей вектора
называется составляющей вектора 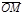 по оси Z, причем
по оси Z, причем 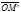 =
= 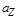
 , где
, где  - орт оси Z.
Замечание. Проекция
- орт оси Z.
Замечание. Проекция 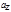 вектора
вектора 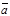 на ось Z положительна, если jÎ[0, p/2) (рис. 12а), равна нулю, если j=p/2, и отрицательна, если jÎ(p/2, p] (рис. 12б). Проекции равных векторов на одну и ту же ось равны между собой.
Теорема 3. Проекция суммы векторов на данную ось равна сумме проекций этих векторов на ту же ось, т.е.
на ось Z положительна, если jÎ[0, p/2) (рис. 12а), равна нулю, если j=p/2, и отрицательна, если jÎ(p/2, p] (рис. 12б). Проекции равных векторов на одну и ту же ось равны между собой.
Теорема 3. Проекция суммы векторов на данную ось равна сумме проекций этих векторов на ту же ось, т.е. 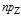 (
(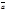 +
+  +
+ 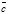 )=
)= 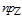
 +
+ 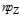
 +
+ 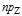
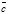 .
Доказательство.
Пусть заданы векторы
.
Доказательство.
Пусть заданы векторы 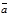 ,
, 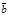 ,
, 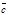 , суммой которых является вектор
, суммой которых является вектор 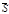 (рис.13). Тогда имеем
(рис.13). Тогда имеем 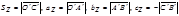 .
Однако
.
Однако 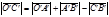 , откуда и получаем
, откуда и получаем 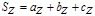 .
.
 Теорема 4. При умножении вектора на число его проекция на данную ось умножается на то же число, т.е.
Теорема 4. При умножении вектора на число его проекция на данную ось умножается на то же число, т.е. 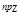 (l
(l 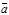 )=l
)=l 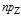
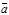 .
Доказательство.
Из определения проекции вектора на ось Z имеем:
.
Доказательство.
Из определения проекции вектора на ось Z имеем: 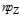
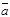 =
= 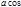 j1,
j1, 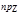 (l
(l 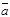 )=|l|
)=|l| 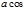 j2, где j1, j2 - значения углов, которые составляют векторы
j2, где j1, j2 - значения углов, которые составляют векторы  и l
и l  с осью Z. В случае l>0, cos j1=cos j2, получаем
с осью Z. В случае l>0, cos j1=cos j2, получаем 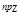 l
l  =l
=l 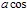 j1=l
j1=l 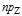
 .
Если же l<0, - cos j1=cos j2, то
.
Если же l<0, - cos j1=cos j2, то 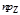 l
l  =|l|
=|l| 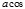 j2=-l
j2=-l  (-cos j1)=l
(-cos j1)=l 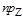
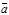 . При l=0 имеем
. При l=0 имеем 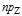 l
l  =l
=l 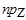
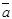 =0.
Теорема доказана.
Свойства проекции
=0.
Теорема доказана.
Свойства проекции
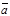 и
и 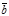 называется число, равное произведению модулей этих векторов и косинуса угла между ними.
Скалярное произведение векторов
называется число, равное произведению модулей этих векторов и косинуса угла между ними.
Скалярное произведение векторов 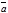 и
и 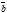 обозначается символом
обозначается символом 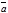
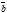 или (
или (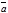 ,
, 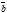 ), т.е. (
), т.е. (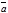 ,
, 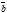 )=ab cosj (рис. 3).
)=ab cosj (рис. 3).
 Вспоминая понятие проекции вектора на ось, можно заключить следующее: скалярное произведение двух векторов
Вспоминая понятие проекции вектора на ось, можно заключить следующее: скалярное произведение двух векторов  и
и  равно длине одного из них умноженной на проекцию другого на направление первого, т.е. (
равно длине одного из них умноженной на проекцию другого на направление первого, т.е. ( ,
,  )=
)= 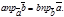 Свойства скалярного произведения векторов:
1. (
Свойства скалярного произведения векторов:
1. (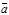 ,
, 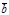 )=(
)=(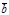 ,
, 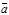 ) - следствие определения,
2.
) - следствие определения,
2. 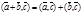 - так как
- так как 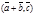 =
= 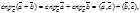 3.
3. 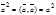 - так как
- так как  ,
4.
,
4. 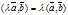 - так как
- так как 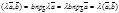 ,
5.
,
5. 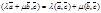 - следствие свойств 2 и 4.
Заметим, что косинус угла j между не нулевыми векторами
- следствие свойств 2 и 4.
Заметим, что косинус угла j между не нулевыми векторами 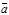 и
и 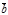 находится по формуле Cos j=
находится по формуле Cos j= 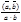 (2)
Из равенства (3.2) следует, что ненулевые векторы
(2)
Из равенства (3.2) следует, что ненулевые векторы 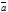 и
и 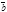 перпендикулярны лишь в том случае, если их скалярное произведение равно нулю, т.е. (
перпендикулярны лишь в том случае, если их скалярное произведение равно нулю, т.е. (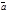 ,
, 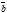 )=0; Cos j=0; j=p/2.
Замечание. Нулевой вектор считается перпендикулярным любому другому вектору.
Некоторые следствия.
1.Проекция вектора
)=0; Cos j=0; j=p/2.
Замечание. Нулевой вектор считается перпендикулярным любому другому вектору.
Некоторые следствия.
1.Проекция вектора  на направление вектора
на направление вектора  равна скалярному произведению вектора
равна скалярному произведению вектора  на орт вектора
на орт вектора  .
Действительно, если векторы
.
Действительно, если векторы  и
и  образуют между собой угол j, то
образуют между собой угол j, то 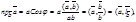 где
где 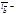 орт вектора
орт вектора 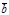 .
2. Скалярное произведение двух векторов равно сумме произведений их соответствующих координат.
На самом деле, если векторы
.
2. Скалярное произведение двух векторов равно сумме произведений их соответствующих координат.
На самом деле, если векторы 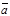 и
и 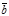 заданы в координатной форме, т.е.
заданы в координатной форме, т.е. 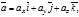
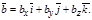 Тогда имея в виду свойства скалярного произведения, и т.к.
Тогда имея в виду свойства скалярного произведения, и т.к.
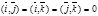 ,
, 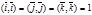 , получим
, получим
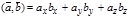 .
3. Косинус угла j между двумя векторами
.
3. Косинус угла j между двумя векторами 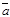 и
и 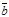 , заданных координатами, определяется по формуле
, заданных координатами, определяется по формуле 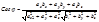 . Данная формула является следствием (2)
4. Два вектора коллинеарны в том и только в том случае, если их соответствующие координаты пропорциональны. Действительно, условие коллинеарности векторов
. Данная формула является следствием (2)
4. Два вектора коллинеарны в том и только в том случае, если их соответствующие координаты пропорциональны. Действительно, условие коллинеарности векторов 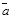 и
и 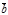
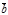 =
= 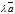 в координатной форме имеет вид
в координатной форме имеет вид
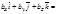
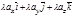 . Из этого равенства следует наше утверждение, так как
. Из этого равенства следует наше утверждение, так как
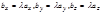 .
Верно и обратное.
Векторное произведение двух векторов
Предварительно введем понятие правой тройки векторов. Три вектора
.
Верно и обратное.
Векторное произведение двух векторов
Предварительно введем понятие правой тройки векторов. Три вектора 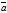 ,
, 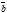 ,
, 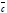 образуют правую тройку, если движение вектора
образуют правую тройку, если движение вектора 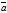 к вектору
к вектору 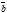 по меньшему углу совершается против часовой стрелки, при наблюдении с конца вектора
по меньшему углу совершается против часовой стрелки, при наблюдении с конца вектора 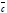 .
Например, орты
.
Например, орты 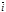 ,
, 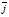 ,
, 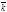 правой системы координат образуют правую тройку векторов. Векторным произведением двух векторов
правой системы координат образуют правую тройку векторов. Векторным произведением двух векторов 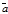 и
и  называется третий вектор
называется третий вектор 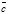 , обозначаемый символом
, обозначаемый символом 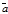 ´
´  и удовлетворяющий условиям:
1.Модуль вектора
и удовлетворяющий условиям:
1.Модуль вектора 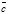 равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах 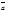 и
и 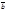 т.е.,
т.е., 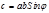 , где j -угол между этими векторами.
2. Вектор
, где j -угол между этими векторами.
2. Вектор 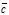 ортогонален векторам
ортогонален векторам 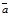 и
и 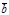 .
3. Тройка векторов
.
3. Тройка векторов 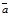 ,
, 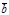 ,
, 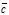 правая.
Свойства векторного произведения.
1.
правая.
Свойства векторного произведения.
1. 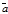 ´
´  =-
=-  ´
´ 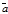 . Действительно, модуль векторного произведения
. Действительно, модуль векторного произведения  ´
´ 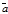 не меняется, т.к. численно равен площади параллелограмма, построенного на векторах
не меняется, т.к. численно равен площади параллелограмма, построенного на векторах 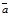 и
и 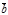 ; направление
; направление 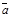 ´
´ 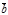 противоположно направлению
противоположно направлению 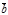 ´
´ 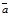 , т.к. движение от вектора
, т.к. движение от вектора  к вектору
к вектору 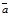 по меньшему углу с конца
по меньшему углу с конца  вектора -(
вектора -(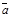 ´
´ 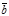 ) видно по направлению против часовой стрелки, (рис. 4).
2.
) видно по направлению против часовой стрелки, (рис. 4).
2. 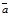 ´
´ 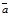 =
=  .
Указанное равенство следует из определения.
Замечание: Для того чтобы векторы были коллинеарны необходимо и достаточно, чтобы их векторное произведение было равно нуль вектору, т.е.
.
Указанное равенство следует из определения.
Замечание: Для того чтобы векторы были коллинеарны необходимо и достаточно, чтобы их векторное произведение было равно нуль вектору, т.е. 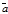 ´
´  =
=  .
3.
.
3. 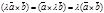 .
Докажем равенство
.
Докажем равенство 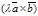 =
= 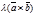 при l>0.
Пусть (
при l>0.
Пусть (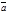 ´
´ 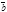 )=
)= 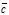 и |
и | 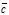 |=abSinj. Тогда вектор
|=abSinj. Тогда вектор 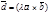 имеем то же направление, что и вектор
имеем то же направление, что и вектор 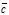 . Но
. Но 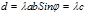 , значит
, значит 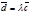 или
или 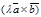 =
= 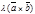 . Очевидно, что
. Очевидно, что 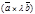 =
= 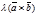 .
4.Для любых векторов
.
4.Для любых векторов 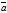 ,
, 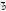 ,
, 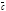 имеет место равенство (
имеет место равенство (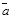 +
+ 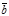 )´
)´ 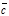 =
= 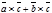 . Рассмотрим частный случай: пары векторов
. Рассмотрим частный случай: пары векторов 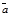 ,
, 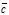 и
и 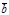 ,
, 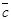 -правые. В этом случае векторы (
-правые. В этом случае векторы (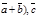 также образуют правую пару. Тогда векторы
также образуют правую пару. Тогда векторы 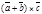 ,
, 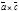 ,
, 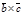 коллинеарны и одинаково направлены. И нам остается доказать, что модуль вектора
коллинеарны и одинаково направлены. И нам остается доказать, что модуль вектора 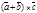 равен сумме модулей векторов
равен сумме модулей векторов 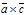 и
и 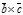 , т.е. |
, т.е. | 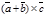 |=|
|=| 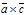 |+|
|+| 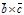 |.
Рассматривая соответствующие параллелограммы, (рис. 5), имеем
|.
Рассматривая соответствующие параллелограммы, (рис. 5), имеем 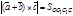 ,
, 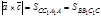 .
.
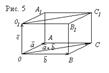 Так как
Так как 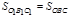 , то имеет место равенство площадей
, то имеет место равенство площадей
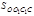
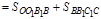 . Откуда |
. Откуда | 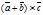 |=|
|=| 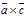 |+|
|+|  |, а значит
|, а значит
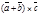 =
= 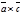 +
+ 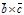 . Таким образом векторное произведение сумм векторов осуществляется
по правилу умножения многочленов.
5.Векторное произведение в координатах.
Пусть даны два вектора
. Таким образом векторное произведение сумм векторов осуществляется
по правилу умножения многочленов.
5.Векторное произведение в координатах.
Пусть даны два вектора 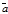 и
и 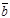 в координатах, т.е.
в координатах, т.е.
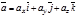 ,
, 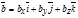 .
Тогда, используя свойства векторного произведения и условия
.
Тогда, используя свойства векторного произведения и условия
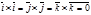 ,
, 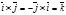 ,
,
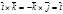 ,
, 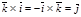 получим
получим 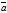 ´
´ 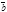 =
= 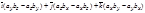 .
Или
.
Или 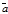 ´
´  =
= 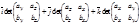 ,
откуда
,
откуда 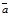 ´
´ 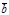 =
= 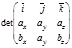 .
Замечание. Так как |
.
Замечание. Так как | 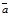 ´
´ 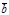 |2 можно представить в виде
|
|2 можно представить в виде
| 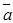 ´
´ 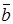 |2=
|2= 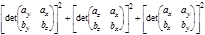 ,
то площадь S треугольника, построенного на векторах
,
то площадь S треугольника, построенного на векторах 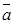 и
и 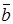 можно вычислить по формуле S=1/2|
можно вычислить по формуле S=1/2| 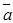 ´
´ 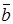 | или
| или
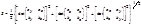
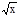 , X={x| x³0}, Y={y| y³0}.
Способы задания функций
1. Аналитическое задание. Если указана совокупность операций, которые надо произвести над аргументом x, чтобы получить значение функции y, то говорят, что функция задана аналитически.
1). Явное задание: y=f(x).
Например, y=
, X={x| x³0}, Y={y| y³0}.
Способы задания функций
1. Аналитическое задание. Если указана совокупность операций, которые надо произвести над аргументом x, чтобы получить значение функции y, то говорят, что функция задана аналитически.
1). Явное задание: y=f(x).
Например, y= 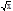 +1, x³0; y=x2-5x-1.
2). Неявное задание: уравнение F(x,y)=0, при некоторых условиях, задает функцию y=f(x), если F(x, f(x))º0.
Например: Уравнение x2+y2=1 при y³0 задает функцию y=
+1, x³0; y=x2-5x-1.
2). Неявное задание: уравнение F(x,y)=0, при некоторых условиях, задает функцию y=f(x), если F(x, f(x))º0.
Например: Уравнение x2+y2=1 при y³0 задает функцию y= 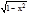 .
2. Табличное задание. На практике часто зависимость одной величины от другой находят опытным путем. В этом случае получается таблица, в которой даются значения функции для конечного множества значений аргумента.
3. Графическое задание. Графиком функции y = f(x) называется геометрическое место точек плоскости OXY
вида M(x,f(x)), где x - произвольное
значение из области определения функции.
Указанное геометрическое место точек, как правило, образует некоторую кривую l.
В этом случае задание кривой l определяет отображение области определения на область изменения функции f(x) (см. Рис).
4. Словесное или описательное задание. В этом случае функциональная зависимость выражается некоторым словесным утверждением.
Например: Функция [x] есть целая часть числа x
Функция {x} есть дробная часть числа x
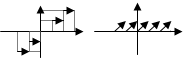
Графики функций y=[x] и y = {x} ºx-[x].
1. Заметим, что [x] означает целую часть числа x, т.е. [x]=n, если x=n+r, где 0£ r <1, причем данная функция определена при любом значении x из R.
Рассматривая промежутки изменения x вида n£x<n+1 при nÎZ, получим, что [x]=n. Поэтому нетрудно построить график y=[x].
2. Запишем выражение x-[ x ] на промежутке x Î [n; n + 1), тогда y=x-[x]=n+r-n=r. Следовательно, значение функции в точке n+r равно дробной части числа x, т.е. yÎ[0;1).
.
2. Табличное задание. На практике часто зависимость одной величины от другой находят опытным путем. В этом случае получается таблица, в которой даются значения функции для конечного множества значений аргумента.
3. Графическое задание. Графиком функции y = f(x) называется геометрическое место точек плоскости OXY
вида M(x,f(x)), где x - произвольное
значение из области определения функции.
Указанное геометрическое место точек, как правило, образует некоторую кривую l.
В этом случае задание кривой l определяет отображение области определения на область изменения функции f(x) (см. Рис).
4. Словесное или описательное задание. В этом случае функциональная зависимость выражается некоторым словесным утверждением.
Например: Функция [x] есть целая часть числа x
Функция {x} есть дробная часть числа x
Графики функций y=[x] и y = {x} ºx-[x].
1. Заметим, что [x] означает целую часть числа x, т.е. [x]=n, если x=n+r, где 0£ r <1, причем данная функция определена при любом значении x из R.
Рассматривая промежутки изменения x вида n£x<n+1 при nÎZ, получим, что [x]=n. Поэтому нетрудно построить график y=[x].
2. Запишем выражение x-[ x ] на промежутке x Î [n; n + 1), тогда y=x-[x]=n+r-n=r. Следовательно, значение функции в точке n+r равно дробной части числа x, т.е. yÎ[0;1).
 |
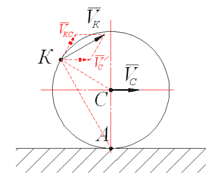
Первый замечательный предел. 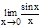 =1
=1
Рассмотрим тригонометрический круг. Имеем
|AC|=sin x
|BmC|=x
BD=tg x
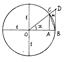 Очевидно, что sin x< x <tg x (при 0< x <p/2).
Очевидно, что sin x< x <tg x (при 0< x <p/2).
Разделим неравенство на sin x¹0, тогда
1< 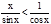 или 1>
или 1> 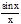 >cos x
>cos x
0> 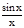 -1>cos x-1; 0< 1-
-1>cos x-1; 0< 1- 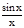 <2sin2
<2sin2 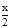 <2×
<2× 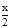 ×
× 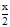 =
= 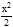
Так как 0 и 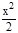 есть бесконечно малые функции при х®0, то и 1-
есть бесконечно малые функции при х®0, то и 1- 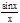 при õ®0 бесконечно малая функции. Значит
при õ®0 бесконечно малая функции. Значит 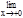
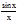 =1.
=1.
Замечание. Доказательство проведено для х>0. Однако, если х<0, то под знаком предела можно сделать замену х=-t, t®+0: 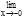
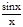 =
= 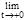
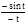 =
= 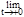
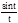 =1.
=1.
Следовательно 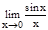 =1
=1
|
|

 2015-04-30
2015-04-30 254
254