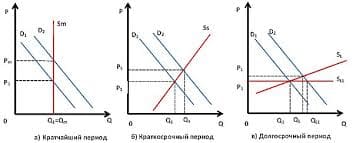
1. Если и  , то
, то
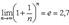
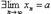
2. Монотонная и ограниченная последовательность имеет предел.
3. Числовая последовательность (xn) имеет конечный предел тогда и только тогда, когда 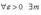
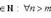
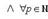
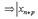
 Это свойство можно строго сформулировать математически и оно имеет большое значение в математике.
Определение предела (по Коши). Функция f(x) хÎХ имеет своим пределом число А при стремлении x к предельной точке х0 множества Х, если для каждого числа e>0 существует число d(e)>0 такое, что при всех х из окрестности |x-x0|<d, x¹x0 имеет место неравенство |f(x)-A|<e.
Символически этот факт записывают в виде
Это свойство можно строго сформулировать математически и оно имеет большое значение в математике.
Определение предела (по Коши). Функция f(x) хÎХ имеет своим пределом число А при стремлении x к предельной точке х0 множества Х, если для каждого числа e>0 существует число d(e)>0 такое, что при всех х из окрестности |x-x0|<d, x¹x0 имеет место неравенство |f(x)-A|<e.
Символически этот факт записывают в виде 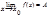 .
Геометрическая интерпретация.
.
Геометрическая интерпретация.
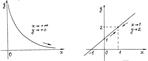
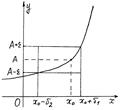 Если функция у=f(x) хÎХ имеет своим пределом число А при х®х0, то разность значений функции и ее предела А достаточно мала, если значение аргумента х близко к х0.
Геометрически это означает, что график функции y=f(x) виден в «окошке» плоскости OXY c координатами: хÎ(х0-d; х0+d), х¹х0, d=min(d1, d2); yÎ(A-e; A+e), А - предел функции, e - любое положительное число.
Особо отметим, что график функции может «выйти» из указанного «окошка» только через боковые стороны. Только через них!
Отметим еще одну особенность: при рассмотрении предела функции в точке х0 само значение функции в точке х0 исследователя не интересует. Это значение f(x0) может быть, в общем случае, равным А или не равным А, или, наконец, функция f(x) в точке х0 может быть не определена.
Определение предела (по Гейне). Функция f(x) хÎХ имеет своим пределом число А при стремлении х к предельной точке х0, если для любой последовательности xn сходящейся к х0, причем xn¹х0 (xnÎ X) последовательность f(xn) сходится к А.
Символическая запись.
Если функция у=f(x) хÎХ имеет своим пределом число А при х®х0, то разность значений функции и ее предела А достаточно мала, если значение аргумента х близко к х0.
Геометрически это означает, что график функции y=f(x) виден в «окошке» плоскости OXY c координатами: хÎ(х0-d; х0+d), х¹х0, d=min(d1, d2); yÎ(A-e; A+e), А - предел функции, e - любое положительное число.
Особо отметим, что график функции может «выйти» из указанного «окошка» только через боковые стороны. Только через них!
Отметим еще одну особенность: при рассмотрении предела функции в точке х0 само значение функции в точке х0 исследователя не интересует. Это значение f(x0) может быть, в общем случае, равным А или не равным А, или, наконец, функция f(x) в точке х0 может быть не определена.
Определение предела (по Гейне). Функция f(x) хÎХ имеет своим пределом число А при стремлении х к предельной точке х0, если для любой последовательности xn сходящейся к х0, причем xn¹х0 (xnÎ X) последовательность f(xn) сходится к А.
Символическая запись. 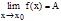 :
1. По Коши: для " e>0, $ d(e, x0)>0, что при |x-x0|<d(e), x¹x0 => |f(x)-A|<e.
2. По Гейне: для " xn®x0, xn¹x0 => f(xn)®A.
Отметим, что определения предела функции в точке по Коши и по Гейне -
эквивалентны.
Сформулируем далее следующие утверждение: число А не является пределом функции f(x) в точке х=х0.
Данное утверждение обычно называют отрицанием предела.
Отрицание предела.
:
1. По Коши: для " e>0, $ d(e, x0)>0, что при |x-x0|<d(e), x¹x0 => |f(x)-A|<e.
2. По Гейне: для " xn®x0, xn¹x0 => f(xn)®A.
Отметим, что определения предела функции в точке по Коши и по Гейне -
эквивалентны.
Сформулируем далее следующие утверждение: число А не является пределом функции f(x) в точке х=х0.
Данное утверждение обычно называют отрицанием предела.
Отрицание предела. 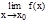 ¹А.
По Коши: $ e0>0 такое, что для " d>0 существует точка х*ÎХ такая, что |x*-x0|<d, x*¹x0, но |f(x*)-A|³e0.
По Гейне: $ xn*®x0, xn*¹x0, что f(xn*) / A.
¹А.
По Коши: $ e0>0 такое, что для " d>0 существует точка х*ÎХ такая, что |x*-x0|<d, x*¹x0, но |f(x*)-A|³e0.
По Гейне: $ xn*®x0, xn*¹x0, что f(xn*) / A.
 и
и 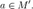 .
1.Одна и та же функция в одной и той же точке может иметь только один предел.
.
1.Одна и та же функция в одной и той же точке может иметь только один предел. 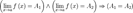 2.Сходящаяся функция локально сохраняет знак. Более обще,
2.Сходящаяся функция локально сохраняет знак. Более обще, 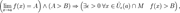 где
где 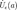 — проколотая окрестность точки a.
3.В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
— проколотая окрестность точки a.
3.В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки: 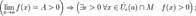 4.Сходящаяся функция локально ограничена в окрестности предельной точки:
4.Сходящаяся функция локально ограничена в окрестности предельной точки: 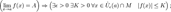 5.Отделимость от нуля функций, имеющих предел, отличный от нуля.
5.Отделимость от нуля функций, имеющих предел, отличный от нуля. 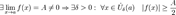 6.Операция взятия предела сохраняет нестрогие неравенства.
6.Операция взятия предела сохраняет нестрогие неравенства. 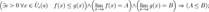 7. Предел суммы равен сумме пределов:
7. Предел суммы равен сумме пределов:  8. Предел разности равен разности пределов:
8. Предел разности равен разности пределов: 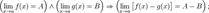 9. Предел произведения равен произведению пределов:
9. Предел произведения равен произведению пределов: 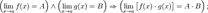 10. Предел частного равен частному пределов.
10. Предел частного равен частному пределов. 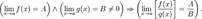 Второй замечательный предел.
Второй замечательный предел. 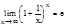 Мы уже встречались ранее с пределом
Мы уже встречались ранее с пределом 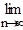 (1+1/n)n=e при nÎN. Очевидно
(1+1/n)n=e при nÎN. Очевидно 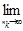 (1+1/nk)nk=e, при nkÎN, т.к. последовательность (1+1/nk)nkявляется подпоследовательностью сходящейся к е, последовательности (1+1/n)n.
Возьмем далее произвольную последовательность хк сходящуюся к +¥, т.е. хк®+¥, при к®¥.
Тогда имеем nk£xk<nk+1, где nk=[xk], а также
(1+1/nk)nk=e, при nkÎN, т.к. последовательность (1+1/nk)nkявляется подпоследовательностью сходящейся к е, последовательности (1+1/n)n.
Возьмем далее произвольную последовательность хк сходящуюся к +¥, т.е. хк®+¥, при к®¥.
Тогда имеем nk£xk<nk+1, где nk=[xk], а также 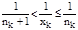 ;
; 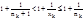 ;
; 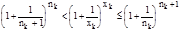 .
То есть
.
То есть 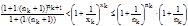 . Пределы левой и правой частей при к®¥ равны е, т.к. nk®+¥ (очевидно и хк®+¥) и
. Пределы левой и правой частей при к®¥ равны е, т.к. nk®+¥ (очевидно и хк®+¥) и 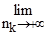 (1+1/nk)nk=e. Откуда по теореме о зажатой последовательности имеем
(1+1/nk)nk=e. Откуда по теореме о зажатой последовательности имеем
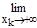 (1+1/хk)хk=e при хк®+¥.
Тогда по определению предела по Гейне получаем, что
(1+1/хk)хk=e при хк®+¥.
Тогда по определению предела по Гейне получаем, что
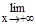 (1+1/х)х=e - 2ойзамечательный предел.
Имеет место также равенство
(1+1/х)х=e - 2ойзамечательный предел.
Имеет место также равенство 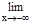 (1+1/х)х=e т.к. сделав замену -х=t, получим:
(1+1/х)х=e т.к. сделав замену -х=t, получим: 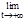 (1-1/t)-t=
(1-1/t)-t= 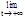
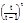 =
= 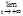
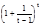 =
= 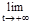
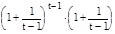 = e
= e
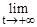
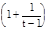 =e.
Итак
=e.
Итак 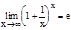 Замечание.
Следует отметить, что
Замечание.
Следует отметить, что 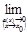 (1+a(х))1/a(х)=е;
(1+a(х))1/a(х)=е;
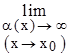 (1+1/a(х))a(х)=е
Не забудьте!!! В формуле 2 огозамечательного предела всегда «добавка» к единице является бесконечно малой, а показатель степени является обратной величиной этой бесконечно малой.
Определение непрерывности функции в точке.
Предположим, что нам задана функция f(x), определенная в некоторой области X={x}, причем полагаем, что предельная точка х=х0 является внутренней точкой множества Х.
Замечание. При определении предела функции было не обязательно, чтобы предельная точка х=х0 принадлежала множеству области определения f(x).
Определение. Функция f(x) называется непрерывной в точке х=х0, если она имеет этой в точке предел равный значению f(x0), т.е.
(1+1/a(х))a(х)=е
Не забудьте!!! В формуле 2 огозамечательного предела всегда «добавка» к единице является бесконечно малой, а показатель степени является обратной величиной этой бесконечно малой.
Определение непрерывности функции в точке.
Предположим, что нам задана функция f(x), определенная в некоторой области X={x}, причем полагаем, что предельная точка х=х0 является внутренней точкой множества Х.
Замечание. При определении предела функции было не обязательно, чтобы предельная точка х=х0 принадлежала множеству области определения f(x).
Определение. Функция f(x) называется непрерывной в точке х=х0, если она имеет этой в точке предел равный значению f(x0), т.е. 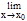 f(x)=f(x0).
Определение по Коши. Функция f(x) непрерывна в точке х=х0,
если по " e>0, $ d(e)>0 такое, что при всех х из |x-x0|< d => |f(x)-f(x0)|< e.
Определение по Гейне. Функция f(x) непрерывна в точке х=х0, если для любой сходящейся к х0 последовательности xn®x0, имеем f(xn)®f(x0).
Важно отметить, что равенство
f(x)=f(x0).
Определение по Коши. Функция f(x) непрерывна в точке х=х0,
если по " e>0, $ d(e)>0 такое, что при всех х из |x-x0|< d => |f(x)-f(x0)|< e.
Определение по Гейне. Функция f(x) непрерывна в точке х=х0, если для любой сходящейся к х0 последовательности xn®x0, имеем f(xn)®f(x0).
Важно отметить, что равенство 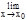 f(x)=f(x0) можно записать в виде
f(x)=f(x0) можно записать в виде 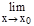 f(x)=f(
f(x)=f(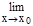 x).
То есть для непрерывных функций возможно переставить местами символы «функция» и «предел», что очень важно при вычислении пределов.
Определению непрерывности функции f(x) в точке х=х0 можно придать другую форму: дадим аргументу х в точке х=х0, приращение Dх=х-х0, тогда разность f(x)-f(x0)=Dy представляет собой приращение функции в точке х=х0, соответствующее приращению аргумента Dх, т.е. DуºDf(x0)=f(x0+Dx)-f(x0).
Из определения непрерывности f(x) следует, что при Dх®0 (х®х0) имеет место Dу®0 (f(x)®f(x0)), т.е.
x).
То есть для непрерывных функций возможно переставить местами символы «функция» и «предел», что очень важно при вычислении пределов.
Определению непрерывности функции f(x) в точке х=х0 можно придать другую форму: дадим аргументу х в точке х=х0, приращение Dх=х-х0, тогда разность f(x)-f(x0)=Dy представляет собой приращение функции в точке х=х0, соответствующее приращению аргумента Dх, т.е. DуºDf(x0)=f(x0+Dx)-f(x0).
Из определения непрерывности f(x) следует, что при Dх®0 (х®х0) имеет место Dу®0 (f(x)®f(x0)), т.е. 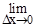 Dу=0.
(
Dу=0.
(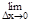 (f(x0+Dх)-f(x0))=0).
Итак, непрерывная в точке функция характеризуется тем, что бесконечно малому приращению аргумента Dх соответствует бесконечно малое приращение функции Dу.
(f(x0+Dх)-f(x0))=0).
Итак, непрерывная в точке функция характеризуется тем, что бесконечно малому приращению аргумента Dх соответствует бесконечно малое приращение функции Dу.
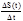 .
Если мы хотим найти скорость точки в данный момент (мгновенную скорость), а именно в момент времени t, нужно вычислить предел
.
Если мы хотим найти скорость точки в данный момент (мгновенную скорость), а именно в момент времени t, нужно вычислить предел 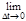 Vср=
Vср= 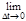
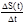 .
Таким образом находим скорость изменения функции S(t) в момент времени t.
б. Линейная плотность стержня.
Если стержень является неоднородным, то очевидной характеристикой стержня является плотность его в данной точке, которая определяется как отношение массы стержня к его длине. Находим среднюю плотность стержня на промежутке [x, x+Dx]
rcр=
.
Таким образом находим скорость изменения функции S(t) в момент времени t.
б. Линейная плотность стержня.
Если стержень является неоднородным, то очевидной характеристикой стержня является плотность его в данной точке, которая определяется как отношение массы стержня к его длине. Находим среднюю плотность стержня на промежутке [x, x+Dx]
rcр= 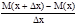 =
= 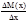 Тогда плотность стержня в точке х выразится пределом
r(х)=
Тогда плотность стержня в точке х выразится пределом
r(х)= 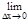 rcр=
rcр= 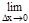
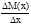 .
в. Задача о касательной к кривой.
Пусть уравнение y=f(x) задает в плоскости Оху, некоторую кривую l. Для данной кривой ставится задача: определить наклон касательной к этой кривой, проведенной в точке (x, f(x)), т.е. определить тангенс угла между касательной и положительным направлением оси Ох. При этом касательной к кривой l в точке (x, f(x)) называется предельное положение секущей, проходящей через точки (x, f(x)) и (x+Dx, f(x+Dx))
при Dх®0.
Находим тангенс угла наклона секущей L:
tg a=
.
в. Задача о касательной к кривой.
Пусть уравнение y=f(x) задает в плоскости Оху, некоторую кривую l. Для данной кривой ставится задача: определить наклон касательной к этой кривой, проведенной в точке (x, f(x)), т.е. определить тангенс угла между касательной и положительным направлением оси Ох. При этом касательной к кривой l в точке (x, f(x)) называется предельное положение секущей, проходящей через точки (x, f(x)) и (x+Dx, f(x+Dx))
при Dх®0.
Находим тангенс угла наклона секущей L:
tg a= 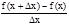 =
= 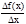
 tg b=
tg b= 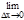
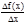 , где b - угол наклона касательной к кривой в точке (x, f(x)), который она составляет с положительным направлением оси Ох. Из приведенных примеров следует, что многие практические задачи физики, геометрии и техники сводятся к вычислению предела частного, в числителе которого стоит приращение функции, а в знаменателе приращение аргумента, вызвавшее это приращение.
Производная функции в точке.
Определение. Производной функции y=f(x) в точке называется предел отношения приращения функции (Dу) в этой точке к соответствующему приращению аргумента (Dх) при стремлении последнего к нулю, то есть
y'(x)=
, где b - угол наклона касательной к кривой в точке (x, f(x)), который она составляет с положительным направлением оси Ох. Из приведенных примеров следует, что многие практические задачи физики, геометрии и техники сводятся к вычислению предела частного, в числителе которого стоит приращение функции, а в знаменателе приращение аргумента, вызвавшее это приращение.
Производная функции в точке.
Определение. Производной функции y=f(x) в точке называется предел отношения приращения функции (Dу) в этой точке к соответствующему приращению аргумента (Dх) при стремлении последнего к нулю, то есть
y'(x)= 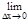
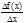 при условии, что этот предел существует. Принято обозначать производную функции у=f(x) в точке х как y'(x) или
при условии, что этот предел существует. Принято обозначать производную функции у=f(x) в точке х как y'(x) или 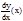 .
Дифференциа́л — линейная часть приращения функции.
Дифференцируемость функции.
Определение. Функция y=f(x) называется дифференцируемой в точке х, если приращение Dу функции f(x) в точке х, отвечающее приращению аргумента Dх, может быть представлено в виде Dу=А×Dх+a(Dх)×Dх, где А - постоянное число (для точки х), не зависящее от Dх; a(Dх) - бесконечно малая функция Dх, т.е.
.
Дифференциа́л — линейная часть приращения функции.
Дифференцируемость функции.
Определение. Функция y=f(x) называется дифференцируемой в точке х, если приращение Dу функции f(x) в точке х, отвечающее приращению аргумента Dх, может быть представлено в виде Dу=А×Dх+a(Dх)×Dх, где А - постоянное число (для точки х), не зависящее от Dх; a(Dх) - бесконечно малая функция Dх, т.е. 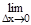 a(Dх)=0.
Иначе говоря, приращение Dу имеет вид Dу=А×Dх+о(Dх).
Далее покажем дифференцируемость некоторых функций.
1. у=х2+2. Dу=(х+Dх)2+2-х2-2=2хDх+Dх2. А=2х; a(Dх)=Dх.
2. у=ln x. Dy=ln(x+Dx)-ln x=ln(1+Dx/x)=Dx/x+о(Dx)
3. у=sin x. Dy=sin(x+Dx)-sin x=2sin(Dx/2)cos(Dx/2+x)=
=2(Dx/2+о(Dx))[cos x+(cos(x+Dx/2)-cos x)]=
=[Dx+2×о(Dx)]cos x-[Dx+2o(Dx)]sin(x+Dx/4)sinDx/2=
=[Dx+2×о(Dx)]cos x-[Dx+2×о(Dx)][Dx/2+о(Dx)]sin(x+Dx/4)=
=cos x Dx+2cos x×о(Dx)-(Dx)2×(f(Dx, x))=cos x Dx+о(Dx).
Теорема. Для того чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно чтобы f(x) имела в этой точке производную.
Доказательство.
1. Необходимость. Пусть y=f(x) в т. х дифференцируема, тогда Dу=А×Dх+о(Dх). Разделим Dу на Dх и вычислим предел частного
a(Dх)=0.
Иначе говоря, приращение Dу имеет вид Dу=А×Dх+о(Dх).
Далее покажем дифференцируемость некоторых функций.
1. у=х2+2. Dу=(х+Dх)2+2-х2-2=2хDх+Dх2. А=2х; a(Dх)=Dх.
2. у=ln x. Dy=ln(x+Dx)-ln x=ln(1+Dx/x)=Dx/x+о(Dx)
3. у=sin x. Dy=sin(x+Dx)-sin x=2sin(Dx/2)cos(Dx/2+x)=
=2(Dx/2+о(Dx))[cos x+(cos(x+Dx/2)-cos x)]=
=[Dx+2×о(Dx)]cos x-[Dx+2o(Dx)]sin(x+Dx/4)sinDx/2=
=[Dx+2×о(Dx)]cos x-[Dx+2×о(Dx)][Dx/2+о(Dx)]sin(x+Dx/4)=
=cos x Dx+2cos x×о(Dx)-(Dx)2×(f(Dx, x))=cos x Dx+о(Dx).
Теорема. Для того чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно чтобы f(x) имела в этой точке производную.
Доказательство.
1. Необходимость. Пусть y=f(x) в т. х дифференцируема, тогда Dу=А×Dх+о(Dх). Разделим Dу на Dх и вычислим предел частного 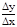 при Dх®0:
при Dх®0:
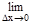
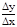 =
= 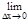 (А+
(А+ 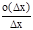 )=А.
С другой стороны
)=А.
С другой стороны 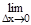
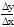 =f '(x). Значит f '(x) существует и равна А.
2. Достаточность. Пусть функция y=f(x) имеет производную, т.е.
=f '(x). Значит f '(x) существует и равна А.
2. Достаточность. Пусть функция y=f(x) имеет производную, т.е. 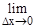
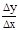 =у'(x), тогда разность функции
=у'(x), тогда разность функции 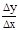 и предела y'(x) есть величина бесконечно малая при Dх®0, т.е.
и предела y'(x) есть величина бесконечно малая при Dх®0, т.е. 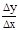 -y'(x)=a(Dх); a(Dх)®0 приDх®0, Dу=y'(x)×Dx+a(Dx)×Dx. Пусть y'(x)=A для точки х, тогда Dу=А×Dх+a(Dх)×Dх.
Теорема доказана.
Теорема. Дифференцируемая в точке х функция y=f(x) непрерывна в этой точке.
Доказательство. Так как Dу=А×Dх+о(Dх) - условие дифференцируемости, то при Dх®0 получаем Dу®0. Последнее означает непрерывность функции f(x) в точке х.
Замечание. Дифференцируемая в точке х=х0 функция у=f(x) имеет в точке (х0; f(x0)) касательную прямую.
-y'(x)=a(Dх); a(Dх)®0 приDх®0, Dу=y'(x)×Dx+a(Dx)×Dx. Пусть y'(x)=A для точки х, тогда Dу=А×Dх+a(Dх)×Dх.
Теорема доказана.
Теорема. Дифференцируемая в точке х функция y=f(x) непрерывна в этой точке.
Доказательство. Так как Dу=А×Dх+о(Dх) - условие дифференцируемости, то при Dх®0 получаем Dу®0. Последнее означает непрерывность функции f(x) в точке х.
Замечание. Дифференцируемая в точке х=х0 функция у=f(x) имеет в точке (х0; f(x0)) касательную прямую.
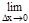
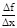 =
= 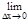 (fj'×jx'+fj' a(Dx)+a(Dj)×
(fj'×jx'+fj' a(Dx)+a(Dj)× 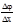 )=fj'×jx'.
Окончательно имеем fx'(j(x))=fj'×jx'.
Производная неявной функции.
Пусть значения двух переменных х и у связаны между собой уравнением вида F(x, y)=0.
Пример: у+
)=fj'×jx'.
Окончательно имеем fx'(j(x))=fj'×jx'.
Производная неявной функции.
Пусть значения двух переменных х и у связаны между собой уравнением вида F(x, y)=0.
Пример: у+ 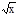 =0, x2+ln y=0.
Определение. Если функция y=f(x), определенная на некотором интервале (a, b) такова, что уравнение F(x, y)=0 при подстановке в него y=f(x) обращается в тождество относительно х, то функция у=f(x) называется неявно заданной уравнением F(x, y)=0.
Частные производные функции z=F(x, y).
Определение. Если существует предел
=0, x2+ln y=0.
Определение. Если функция y=f(x), определенная на некотором интервале (a, b) такова, что уравнение F(x, y)=0 при подстановке в него y=f(x) обращается в тождество относительно х, то функция у=f(x) называется неявно заданной уравнением F(x, y)=0.
Частные производные функции z=F(x, y).
Определение. Если существует предел 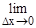
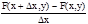 , то он называется частной производной по переменному х функции z=F(x, y) в точке (х, у) и обозначается символами zx' или Fx'(x, y).
Определение. Если существует предел
, то он называется частной производной по переменному х функции z=F(x, y) в точке (х, у) и обозначается символами zx' или Fx'(x, y).
Определение. Если существует предел 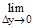
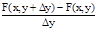 , то он называется частной производной по переменному у функции z=F(x, y) в точке (х, у) и обозначается символами zy' или Fy'(x, y).
Полное приращение F(x, y)
Пусть имеем функцию двух переменных z=F(x, y), где у=f(x) дифференцируемая функция; т.е. F(x, y) является функцией переменного х как сложная функция z=F(x, f(x)). Если переменная х получает приращение Dх, то переменная у=f(x) также принимает приращение Dу в силу непрерывности f(x). Откуда получим:
DF(x)=F(x+Dx, y+Dy)-F(x, y)=F(x+Dx, y+Dy)-F(x, y+Dy)+F(x, y+Dy)-F(x, y)= =DxF(x, y+Dy)+DyF(x, y). тогда после деления равенства на Dх и перехода к пределу при Dх®0 получим:
, то он называется частной производной по переменному у функции z=F(x, y) в точке (х, у) и обозначается символами zy' или Fy'(x, y).
Полное приращение F(x, y)
Пусть имеем функцию двух переменных z=F(x, y), где у=f(x) дифференцируемая функция; т.е. F(x, y) является функцией переменного х как сложная функция z=F(x, f(x)). Если переменная х получает приращение Dх, то переменная у=f(x) также принимает приращение Dу в силу непрерывности f(x). Откуда получим:
DF(x)=F(x+Dx, y+Dy)-F(x, y)=F(x+Dx, y+Dy)-F(x, y+Dy)+F(x, y+Dy)-F(x, y)= =DxF(x, y+Dy)+DyF(x, y). тогда после деления равенства на Dх и перехода к пределу при Dх®0 получим:
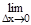
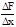 =
= 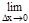
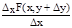 +
+ 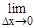
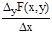 =
= 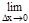
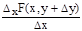 +
+ 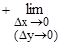
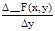 ×
× 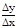 =Fx'(x, y)+Fy'(x, y)×y'(x)
Итак: для того чтобы вычислить производную функции у=f(x), заданной неявно уравнением F(x, y)=0, нужно приравнять нулю производную левой части как производную сложной функции, считая у функцией х, т.е. у=f(x). При этом получим равенство Fx'+Fy'×yx'=0 или yx'=
=Fx'(x, y)+Fy'(x, y)×y'(x)
Итак: для того чтобы вычислить производную функции у=f(x), заданной неявно уравнением F(x, y)=0, нужно приравнять нулю производную левой части как производную сложной функции, считая у функцией х, т.е. у=f(x). При этом получим равенство Fx'+Fy'×yx'=0 или yx'= 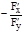 . Fy'¹0.
Здесь Fx' и Fy' - частные производные F(x, y) по переменным х и у соответственно.
Например.
1. х2+у2-а2=0. 2х+2y×y'=0, yx'=-x/y; y¹0.
2. sin x+yx=0. cos x+y+y'×x=0, yx'=
. Fy'¹0.
Здесь Fx' и Fy' - частные производные F(x, y) по переменным х и у соответственно.
Например.
1. х2+у2-а2=0. 2х+2y×y'=0, yx'=-x/y; y¹0.
2. sin x+yx=0. cos x+y+y'×x=0, yx'= 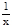 (-y-cos x)=
(-y-cos x)=  (-cos x+
(-cos x+ 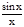 ). x¹0.
). x¹0.
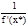 .
Доказательство. Дадим приращение Dу переменной у в точке у*, тогда обратная функция х=j(у) получит соответствующее приращение Dх=Dj(у*). Заметим, что приращения Dх и Dу отличны от нуля, так как функции j(у) и f(x) строго монотонны. Далее составим частное
.
Доказательство. Дадим приращение Dу переменной у в точке у*, тогда обратная функция х=j(у) получит соответствующее приращение Dх=Dj(у*). Заметим, что приращения Dх и Dу отличны от нуля, так как функции j(у) и f(x) строго монотонны. Далее составим частное 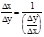 . При переходе к пределу при Dу®0 (очевидно Dх®0), получим xy¢(y*)=
. При переходе к пределу при Dу®0 (очевидно Dх®0), получим xy¢(y*)= 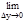
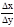 =
= 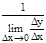 =
= 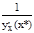 . Следовательно j¢(y)|y=y*=
. Следовательно j¢(y)|y=y*= 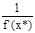 .
Вывод призводных
1. y=logax, y'=
.
Вывод призводных
1. y=logax, y'= 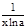 .
Так как Dy=loga(x+Dx)-logax=loga(1+Dx/x), вычислим
.
Так как Dy=loga(x+Dx)-logax=loga(1+Dx/x), вычислим
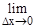
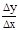 =
= 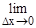
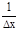 ×loga(1+Dx/x)=
×loga(1+Dx/x)= 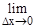
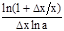 =
= 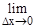
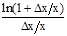
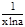 ==
== 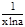 ×
× 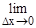
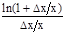 =
= 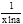 .
2. y=ctg x, y'=
.
2. y=ctg x, y'= 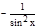 .
Dy=ctg(x+Dx)-ctg x=
.
Dy=ctg(x+Dx)-ctg x= 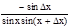 ;
y'=
;
y'= 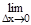
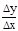 =
= 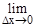
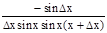 =
= 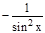 .
3. (arcsin x)'=
.
3. (arcsin x)'= 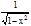 Доказательство. Если у=arcsin x, то обратная функция x=sin y. Причем уÎ(-p/2; p/2), а тогда cos y>0. В силу предыдущей теоремы имеем.
Доказательство. Если у=arcsin x, то обратная функция x=sin y. Причем уÎ(-p/2; p/2), а тогда cos y>0. В силу предыдущей теоремы имеем.
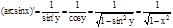 .;
4. (arccos x)'=-
.;
4. (arccos x)'=- 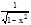 Доказательство. у=arccos x; x=cosy, yÎ(0, p), sin y>0. Тогда
Доказательство. у=arccos x; x=cosy, yÎ(0, p), sin y>0. Тогда
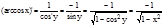 .;
5. (arctg x)'=
.;
5. (arctg x)'= 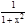 Доказательство. y=arctg x; x=tg y. Поэтому имеем
Доказательство. y=arctg x; x=tg y. Поэтому имеем
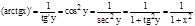 .;
6. (arcctg x)'= -
.;
6. (arcctg x)'= - 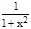 Доказательство. y=arcсtg x; x=сtg y. Поэтому имеем
Доказательство. y=arcсtg x; x=сtg y. Поэтому имеем
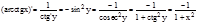 .;
.;
 2015-04-30
2015-04-30 322
322