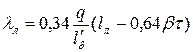Коэффициент магнитной проводимости лобового рассеяния. где q и — число пазов на полюс и фазу и длина лобовой части витка обмотки

, (8.17)

где q и 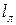— число пазов на полюс и фазу и длина лобовой части витка обмотки;

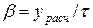— укорочение шага обмотки, для которой прово­дится расчет.

Коэффициент магнитной проводимости дифференциального рас­сеяния для обмоток статора

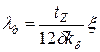. (8.18)

Значение коэффициента ξ зависит от числа q, укорочения шага обмотки и размерных соотношений зубцовых зон и воздушного зазора.

ξ находят следующим образом.

При открытых пазах статора и отсутствии скоса статора или ротора

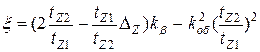. (8.19)

При полузакрытых или полуоткрытых пазах статора с учетом скоса пазов

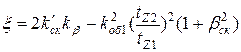. (8.20)

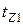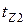В этих формулах и — зубцовые деления статора и ротора;

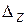определяют по кривой рис. 8.5, а, 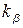определяют по (8.16);

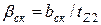— скос пазов, выраженный в долях зубцового де­ления ротора. При отсутствии скоса пазов ;

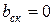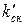определяют по кривым рис. 8.5, б в зависимости от 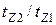и 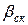(при отсутствии скоса пазов — по кривой, соответствующей ).

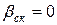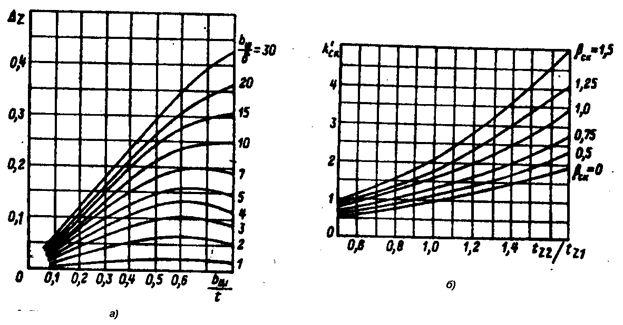
Рис. 8.5. Коэффициенты к расчету проводимости дифференциального рассеяния:

а – коэффициент 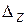в зависимости от размерных соотношени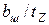й и ;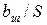

б – коэффициент 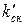в зависимости от соотношения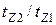

и относительного скоса пазов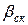

Активное сопротивление фазы короткозамкнутого ротора опреде­ляется следующим образом.

Ток 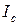называют током ротора и в расчетах обозначают .

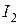Учитывая, что

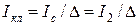, (8.21)

где 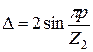, из (8.21), получаем

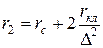; (8.22)

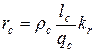; (8.23)

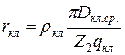. (8.24)

В этих выражениях 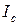— полная длина стержня, равная расстоя­нию между замыкающими кольцами, м;

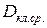— средний диаметр замыкающих колец, м (см. рис. 8.6):

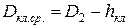; (8.25)

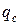— сечение стержня, м2;

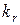— коэффициент увеличения активного со­противления стержня от действия эффекта вытеснения тока; при рас­чете рабочих режимов в пределах изменения скольжения от холостого хода до номинального для всех роторов принимают ;

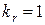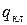— площадь поперечного сечения замыкающего кольца, м2;

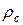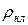и — соответственно удельные сопротивления материала стержня и замыкающих колец, Ом×м, при расчетной температуре.

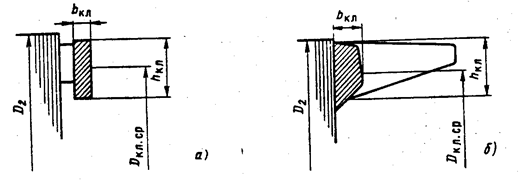
Рис. 8.6. Размеры замыкающих колец короткозамкнутого ротор:

а – со сварной обмоткой; б – с литой обмоткой

Сопротивление 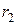для дальнейших расчетов должно быть приве­дено к числу витков первичной обмотки. Выражение коэффициента приведения для сопротивления фазы короткозамкнутого ротора

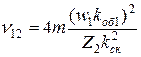. (8.26)

Обычно значения 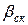выражают в долях зубцового деления ротора 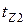. При скосе пазов ротора на одно зубцовое деление стато­ра 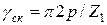. B этом случае в двигателях с 2 p = 2 из-за малости угла 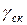принимают .

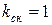Приведенное значение активного сопротивления фазы обмотки короткозамкнутого ротора

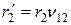. (8.27)

Индуктивное сопротивление обмотки короткозамкнутого ротора определяют по формуле

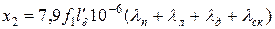, (8.28)

полученной после подстановки в (8.14) значени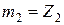й и 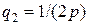обмотки короткозамкнутого ротора и введения дополнительного слагаемого .

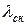Коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора рассчитывают по приведенным в табл. 8.4 формулам в зависимости от конфигурации паза ротора (рис. 8.7).

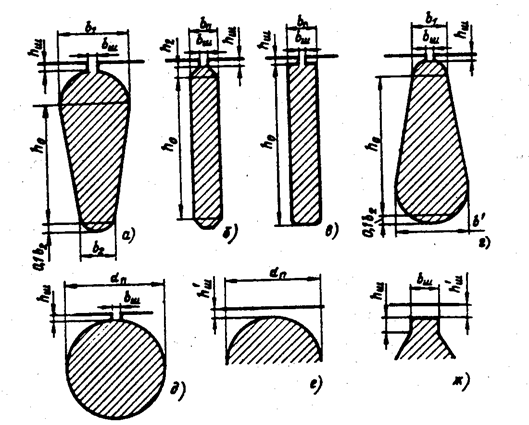
Рис. 8.7. К расчету коэффициентов магнитной проводимости пазового рассеяния короткозамкнутых роторов:

а–д – полузакрытые пазы; е, ж – закрытые пазы

Таблица 8.4. Расчетные формулы для определения коэффициентов

магнитной проводимости пазового рассеяния короткозамкнутых роторов

Рисунок	Расчетные формулы
8.7, а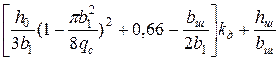
8.7, б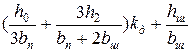
8.7, в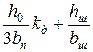
8.7, г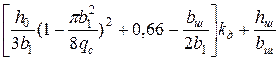
8.7, д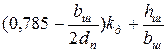

При расчете номинального режима двигателя во всех формулах .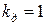

При закрытых пазах ротора любой конфигурации (рис. 8.7, а—д) в расчетных формулах табл. 8.4 нужно при шлицах по рис. 8.7, е слагаемые 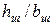заменить на 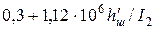, по рис. 8.7, ж — на 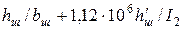, где 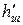— толщина ферромагнит­ной перемычки над пазом, м; 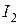— ток ротора, А.

Коэффициент магнитной проводимости лобового рассеяния рассчитывают в зависимости от размеров и расположения замыкающих колец обмотки по сл. формулам.

В роторах с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора (см. рис. 8.6, б), используют формулу

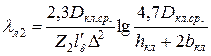. (8.29)

Если замыкающие кольца отставлены от торцов ротора (см. рис. 8.6, а), как, например, в обмотке, выполненной из медных или латунных стержней, впаянных в замыкающие кольца, расчет проводят по формуле

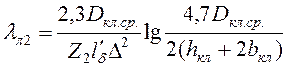. (8.30)

В этих формулах 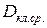— средний диаметр замыкающих колец по (8.25);

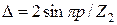— коэффициент приведения токов в кольце к току в стержне;

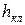и 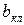— средние высота и ширина колец (см. рис. 8.6);

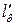— по (8.15).

Коэффициент магнитной проводимости дифференциального рас­сеяния обмотки, короткозамкнутого ротора

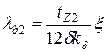, (8.31)

где

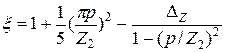; (8.32)

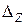находят по кривым рис. 8.5, а.

Как видно из (8.32), при большом числе пазов ротора, приходя­щихся на пару полюсов: 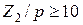, без заметной погрешности можно принять ξ = 1.

Сопротивление взаимной индукции обмоток статора и ротора 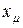по схеме замещения может быть определено как .

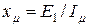В расчетной практике параллельное включение сопротивлени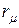й и 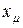оказалось удобнее заменить последовательно включенными сопротивлениям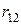и и 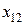(см. рис. 8.1, б), значения которых опре­деляют из условия

,

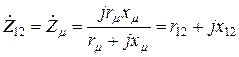откуда

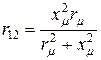и .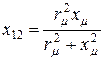

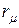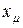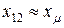Так как в асинхронных машинах ≤ , то , а 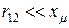. В связи с этим значение 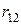не играет заметной роли при анализе процессов в машине, и в расчетах им часто пренебрегают.

Сопротивления 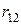и 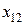с достаточной для обычных расчетов точностью определяют по следующим формулам:

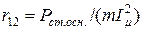; (8.33)

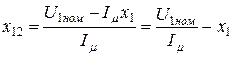. (8.34)