Составление рациональных маршрутов выполняем методом «совмещенной матрицы» по рассмотренному выше алгоритму.
В соответствующие клетки таблицы сводного плана грузопотока (см. табл. 22) из таблицы оптимального плана возврата порожняка (см. табл. 23) переносим данные, характеризующие количество и направление возврата порожних автомобилей. Таким путем построена табл. 24, которая называется «совмещенной матрицей». В табл. 24 цифры, характеризующие количество и направление возврата порожних автомобилей, выделены шрифтом серого цвета.
Таблица 24
Совмещенная матрица
| Поставщики | Потребители | Сумма, т | ||||
| Б1 | Б2 | Б3 | Б4 | Б5 | ||
| А1 | ||||||
| 30 0 | 60 100 | 0 0 | 20 10 | 60 60 | ||
| А2 | ||||||
| 70 120 | 30 30 | 25 0 | 25 0 | 0 0 | ||
| А3 | ||||||
| 20 0 | 40 0 | 110 135 | 80 115 | 0 0 | ||
| Сумма, т |
В некоторых клетках табл. 24 имеются две записи: одна – характеризующая объем перевозок в данном направлении, другая – возврат порожняка в обратном направлении. Меньшая цифра показывает мощность грузопотока по полученному маятниковому маршруту. В рассматриваемом примере таких маршрутов семь: А1-Б2-Б2-А1, А1-Б4-Б4-А1, А1-Б5-Б5-А1, А2-Б1-Б1-А2, А2-Б2-Б2-А2, А3-Б3-Б3-А3, А3-Б4-Б4-А3.
Результаты решения представлены в табл. 29.
Затем выявляем рациональные кольцевые маршруты движения подвижного состава.
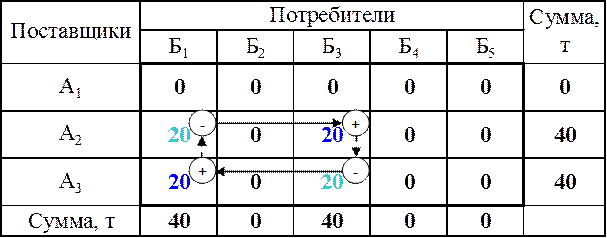
Построение контуров для рассматриваемого примера представлено в табл. 25 – табл. 28. Здесь знаком «+» обозначены клетки, загруженных величинами грузопотоков, а знаком «–» – клетки, загруженных провозной способностью порожнего состава, сплошные стрелки указывают направления груженых ездок, пунктирные стрелки – направления холостых ездок.
Полученные таким образом контуры показывают рациональные кольцевые маршруты движения подвижного состава. Мощность грузопотока на каждом из этих маршрутов определяется наименьшей величиной загрузки клеток, расположенных в углах контура.
Таблица 25
Совмещенная матрица
(маршрут А1-Б1-Б1-А2-А2-Б4-Б4-А3-А3-Б2-Б2-А1)
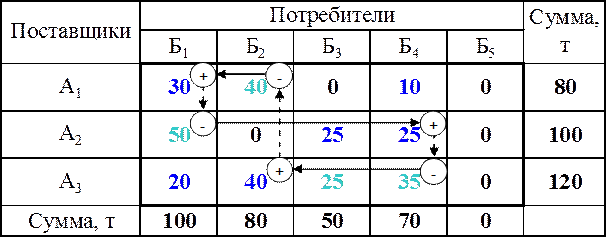
Таблица 26
Совмещенная матрица
(маршрут А1-Б1-Б1-А2-А2-Б3-Б3-А3-А3-Б2-Б2-А1)
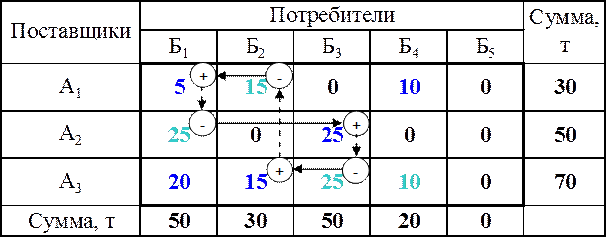
Таблица 27
Совмещенная матрица
(маршрут А1-Б4-Б4-А3-А3-Б2-Б2-А1)
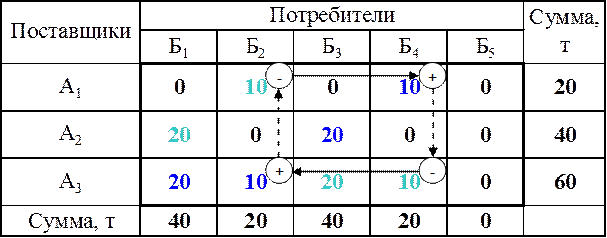
Таблица 28
Совмещенная матрица
(маршрут А2-Б3-Б3-А3-А3-Б1-Б1-А2)
Результаты решения представлены в табл. 29.
4. Рассчитаем потребное количество подвижного состава и его основные технико-эксплуатационные показатели.
Результаты расчета потребного количества подвижного состава по маршрутам и его основные ТЭП представлены в табл. 30.
Расчет ведется в следующем порядке:
1) Рассчитывается время оборотного рейса 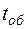 , ч по формуле:
, ч по формуле:
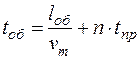 .
.
2) Рассчитывается целое число оборотов ПС на маршруте 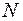 , ед. по формуле:
, ед. по формуле:
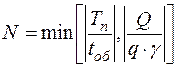 ,
,
где 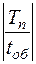 ,
, 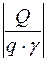 – округленное до целого значение соответствующего аргумента функции.
– округленное до целого значение соответствующего аргумента функции.
3) Рассчитывается фактическое время пребывания подвижного состава на маршруте 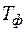 , ч по формуле:
, ч по формуле:
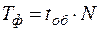 .
.
4) Рассчитывается потребное количество ПС 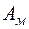 , ед. по формуле:
, ед. по формуле:
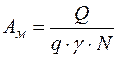 .
.
5) Рассчитывается целое число оборотов последней единицы ПС 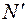 , ед. по формуле:
, ед. по формуле:
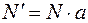 ,
,
где 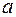 – дробная часть количества единиц ПС
– дробная часть количества единиц ПС 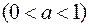 .
.
6) Рассчитывается фактическое время пребывания последней единицы ПС на маршруте 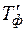 , ч по формуле:
, ч по формуле:
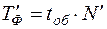 .
.
Таблица 29
Рациональные маршруты
| № маршрута | Вид маршрута | Пункты маршрута | Мощность грузопотока, т | Груженый пробег, км | Общий пробег, км | β |
| Маятниковый | А1-Б2-Б2-А1 | 0,50 | ||||
| Маятниковый | А1-Б4-Б4-А1 | 0,50 | ||||
| Маятниковый | А1-Б5-Б5-А1 | 0,50 | ||||
| Маятниковый | А2-Б1-Б1-А2 | 0,50 | ||||
| Маятниковый | А2-Б2-Б2-А2 | 0,50 | ||||
| Маятниковый | А3-Б3-Б3-А3 | 0,50 | ||||
| Маятниковый | А3-Б4-Б4-А3 | 0,50 | ||||
| Кольцевой | А1-Б1-Б1-А2-А2-Б4-Б4-А3-А3-Б2-Б2-А1 | 0,55 | ||||
| Кольцевой | А1-Б1-Б1-А2-А2-Б3-Б3-А3-А3-Б2-Б2-А1 | 0,59 | ||||
| Кольцевой | А1-Б4-Б4-А3-А3-Б2-Б2-А1 | 0,50 | ||||
| Кольцевой | А2-Б3-Б3-А3-А3-Б1-Б1-А2 | 0,68 | ||||
| Итого: | 0,55 |
Таблица 30
Расчет потребного количества подвижного состава по маршрутам
| № маршрута | Значения ТЭП за один оборот | 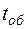 ,
ч ,
ч
| 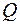 ,
т ,
т
| 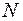 , ед. , ед.
| 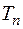 ,
ч ,
ч
| 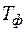 ,
ч ,
ч
| 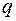 ,
т ,
т
| 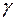
| 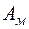 ,
ед. ,
ед.
| Последний автомоб. | |||||
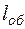 ,
км ,
км
| 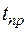 , ч , ч
| 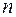 , ед. , ед.
| 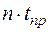 ,
ч ,
ч
| 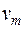 ,
км/ч ,
км/ч
| 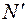 ,
ед. ,
ед.
| 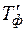 ,
ч ,
ч
| |||||||||
| 0,5 | 0,5 | 1,23 | 7,00 | 7,40 | 2,0 | 7,40 | |||||||||
| 0,5 | 0,5 | 0,90 | 7,00 | 1,80 | 1,0 | 1,80 | |||||||||
| 0,5 | 0,5 | 0,83 | 7,00 | 6,67 | 1,5 | 3,33 | |||||||||
| 0,5 | 0,5 | 0,70 | 7,00 | 7,00 | 1,4 | 2,80 | |||||||||
| 0,5 | 0,5 | 0,70 | 7,00 | 4,20 | 1,0 | 4,20 | |||||||||
| 0,5 | 0,5 | 0,90 | 7,00 | 7,20 | 2,8 | 5,40 | |||||||||
| 0,5 | 0,5 | 0,77 | 7,00 | 6,90 | 1,8 | 5,37 | |||||||||
| 0,5 | 1,5 | 2,83 | 7,00 | 5,67 | 2,5 | 2,83 | |||||||||
| 0,5 | 1,5 | 2,97 | 7,00 | 2,97 | 1,0 | 2,97 | |||||||||
| 0,5 | 2,00 | 7,00 | 4,00 | 1,0 | 4,00 | ||||||||||
| 0,5 | 1,73 | 7,00 | 6,93 | 1,0 | 6,93 |
Примечание. Символы, приведенные в табл. 30 обозначают: 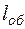 – общий пробег на маршруте за один оборот, км;
– общий пробег на маршруте за один оборот, км; 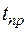 – простой под погрузкой и разгрузкой за одну ездку, ч;
– простой под погрузкой и разгрузкой за одну ездку, ч; 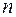 – количество ездок на маршруте за оборот, ед.;
– количество ездок на маршруте за оборот, ед.; 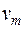 – средняя техническая скорость движения ПС, км/ч;
– средняя техническая скорость движения ПС, км/ч; 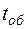 – время оборотного рейса, ч;
– время оборотного рейса, ч; 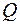 – мощность грузопотока на маршруте, т;
– мощность грузопотока на маршруте, т; 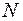 – целое число оборотов ПС на маршруте, ед.;
– целое число оборотов ПС на маршруте, ед.; 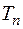 – планируемое время работы ПС на маршруте, ч;
– планируемое время работы ПС на маршруте, ч; 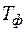 – фактическое время работы ПС на маршруте, ч;
– фактическое время работы ПС на маршруте, ч; 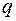 – средняя грузоподъемность единицы ПС, т;
– средняя грузоподъемность единицы ПС, т; 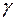 – коэффициент использования грузоподъемности;
– коэффициент использования грузоподъемности; 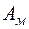 – потребное количество ПС, ед.;
– потребное количество ПС, ед.; 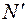 – число оборотов последней единицы ПС, ед.;
– число оборотов последней единицы ПС, ед.; 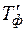 – фактическое время пребывания последней единицы ПС на маршруте, ч.
– фактическое время пребывания последней единицы ПС на маршруте, ч.
5. Вывод: Критерием эффективности решения задачи маршрутизации перевозок массовых грузов является достижение максимально возможной в данных условиях величины коэффициента использования пробега 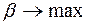 . В рассматриваемом примере коэффициент использования пробега составляет
. В рассматриваемом примере коэффициент использования пробега составляет 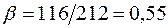 . Таким образом, предлагаемое решение является эффективным.
. Таким образом, предлагаемое решение является эффективным.
 2015-04-30
2015-04-30 1276
1276
