Выражения и формулы

Аналогично тому, как не все возможные последовательности букв алфавита образуют правильно построенные слова, так и в реляционном исчислении не каждая последовательность формул является допустимой. Допустимыми формулами могут быть только недвусмысленные и небессмысленные последовательности. Выражение в реляционном исчислении кортежей имеет следующую общую форму:

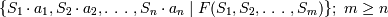
Здесь 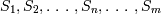переменные кортежа, 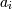- атрибуты отношения, в котором определено значение переменной 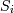, a 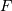— формула.

Формула (таковой считается только правильно построенная формула) состоит из одного или нескольких элементарных выражений, которые могут иметь одну из следующих форм.

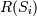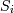• , где — переменная кортежа, a 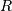— отношение.

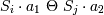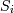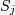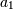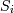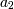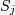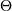• , где и — переменные кортежа, — атрибут отношения, в котором определено значение переменной , — атрибут отношения, в котором определено значение переменной , и — одна из операций сравнения (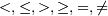); атрибуты 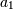и 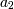должны иметь области определения, для сравнения элементов которых применение знака операции 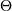является допустимым.

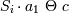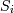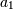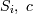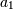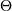• , где — переменная кортежа, — атрибут отношения, в котором определено значение переменной — константа из области определения атрибута и — одна из операций сравнения.

Формулы рекурсивно строятся из элементарных выражений на основе следующих правил.

• Любое элементарное выражение рассматривается как формула.

• Если выражения 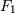и 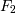являются формулами, то выражения, полученные в результате их конъюнкции 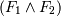, дизъюнкции 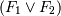и отрицания 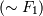, также являются формулами.

• Если выражение 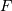является формулой со свободной переменной 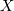, то выражения 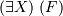и 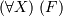также являются формулами.