Вариант 3
Указание : Вариант работы определяется по последним двум цифрам зачётной книжки.
В заданиях 2, 3, 4, 5 номер варианта – k.
| 1. Решить систему алгебраических уравнений: а) методом Крамера; б) методом Гаусса; в) с помощью обратной матрицы. | 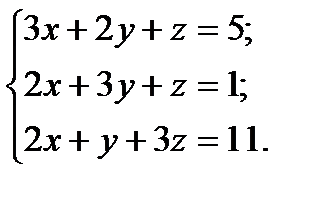
|
2. На плоскости даны прямая l: 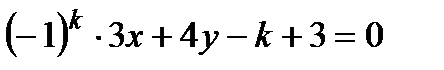 и точка
и точка 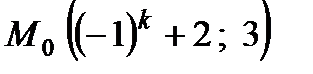 .
.
а) Вычислить расстояние 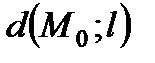 от точки
от точки 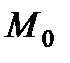 до прямой
до прямой 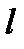 .
.
б) Написать уравнение прямой 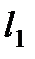 , проходящей через точку
, проходящей через точку 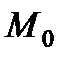 параллельно прямой
параллельно прямой 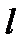 .
.
в) Написать уравнение прямой 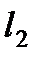 , проходящей через точку
, проходящей через точку 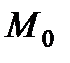 перпендикулярно прямой
перпендикулярно прямой 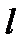 .
.
Сделать чертёж.
3. На плоскости даны две точки 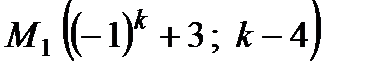 ,
, 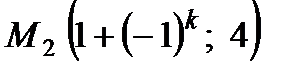 и прямая
и прямая 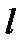 :
: 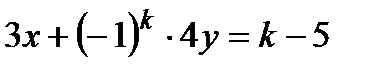 .
.
а) Написать уравнение прямой 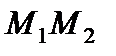 .
.
б) Определить угол между прямыми 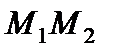 и
и 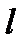 .
.
в) Найти точку пересечения прямых 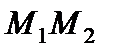 и
и 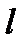 .
.
Сделать чертёж.
4. Даны векторы 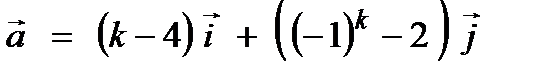 ,
, 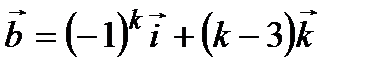 . Найти:
. Найти:
а) скалярное и векторное произведения векторов 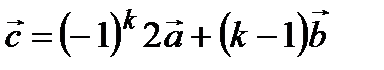 ,
, 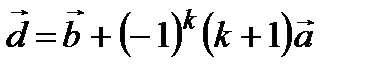 .
.
б) длины векторов 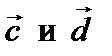 ;
;
в) угол между векторами 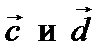 ;
;
г) смешанное произведение векторов 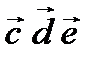 , где
, где 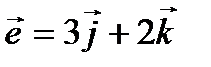 .
.
5. Определить значение комплексного числа, заданного выражением
z = i k + (– i) k + i – k – (– i) – k.
6. Даны комплексные числа: 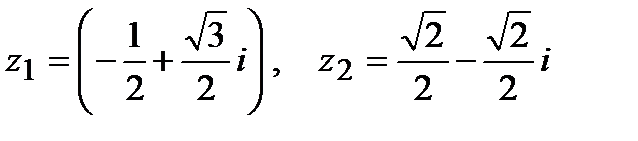 .
.
а) Определить точки плоскости Оху, соответствующие комплексным числам:
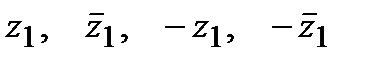 .
.
б) Вычислить  .
.
с) Вычислить 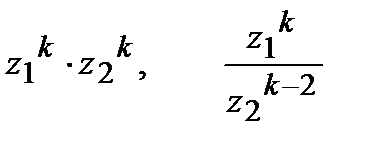 .
.
Представить результаты в тригонометрической форме и в показательной форме.
Вариант 3
7. Найти производную функции: 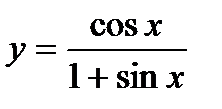 .
.
8. Найти производную 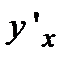 :
: 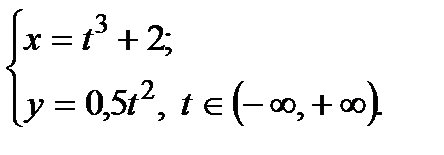
9. Найти вторую производную от функции: 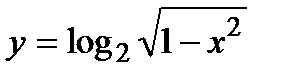 .
.
10. Найти наибольшее и наименьшее значения функции на отрезке: 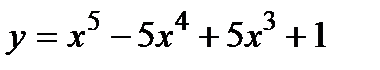 ; [-1; 2].
; [-1; 2].
11. С помощью дифференциального исчисления исследовать и построить график функции: y = 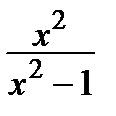 .
.
12. Найти неопределенные интегралы: а) 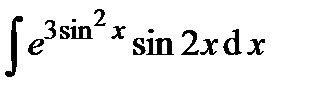 ; б)
; б) 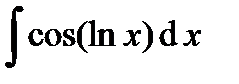
13. Найти полный дифференциал функции и 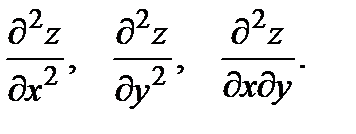
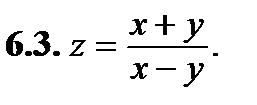
 2015-04-20
2015-04-20 294
294







