Этот метод характеризуется высокой точностью при небольшом числе точек, используемых для расчетов.
Рассмотрим функцию 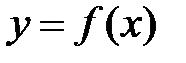 на отрезке
на отрезке 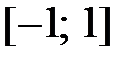 . Для вычисления интеграла по методу Гаусса на отрезке выбираются
. Для вычисления интеграла по методу Гаусса на отрезке выбираются 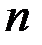 точек.
точек.
Квадратурная формула Гаусса записывается на основе полиномов Лежандра
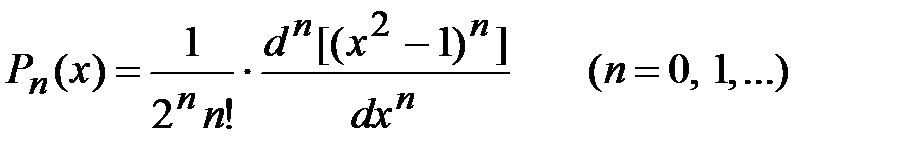 . (6.5)
. (6.5)
Запишем несколько первых полиномов:
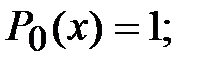
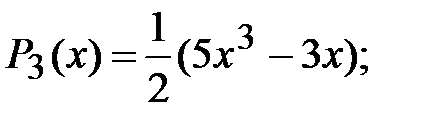
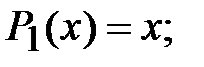
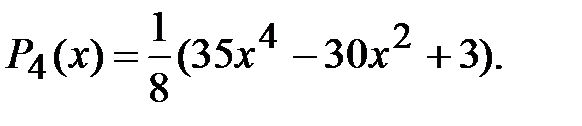
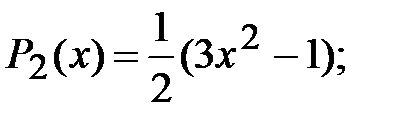
Полиномы Лежандра обладают следующими свойствами:
1) 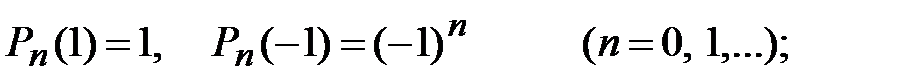
2) 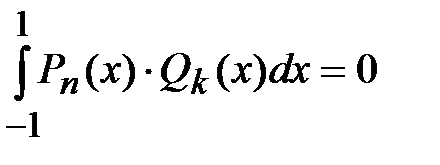 , где
, где 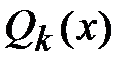 - любой полином степени
- любой полином степени 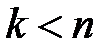 .
.
При вычислении интеграла по квадратурной формуле Гаусса 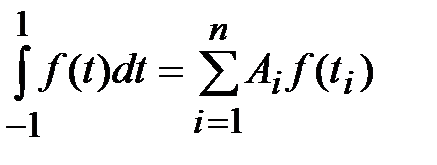 (6.6)
(6.6)
необходимо найти значения коэффициентов 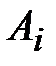 и точки
и точки 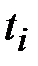 .
.
Точки 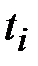 находятся как нули соответствующего полинома Лежандра (степени
находятся как нули соответствующего полинома Лежандра (степени 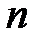 )
)
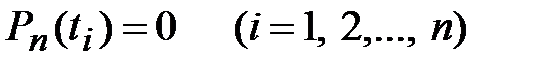 ,
,
которые могут быть найдены, например, методом поразрядного приближения с требуемой точностью 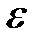 .
.
Для определения коэффициентов 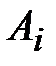 используется система
используется система
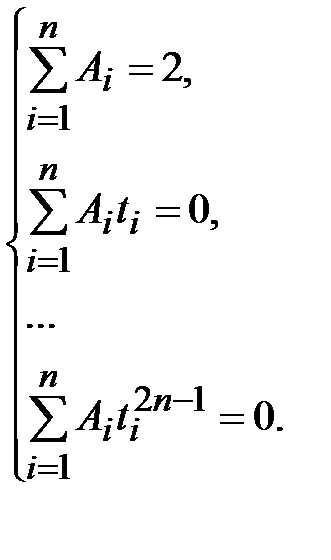
Уравнения данной системы составляются следующим образом:
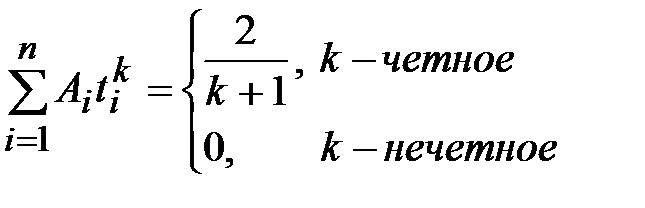
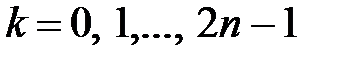 . (6.7)
. (6.7)
Пример. Пусть требуется вывести квадратурную формулу Гаусса с использованием трех вспомогательных точек. Сначала находятся нули 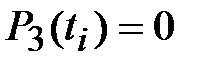 , то есть корни уравнения
, то есть корни уравнения
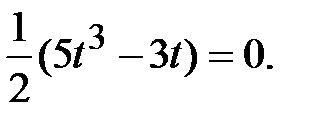
Для этого уравнения корни всегда равны следующим значениям:
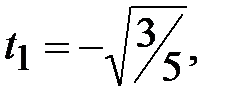
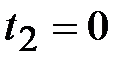 ,
, 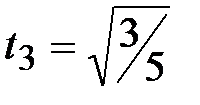 .
.
Коэффициенты 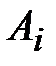 найдем из системы линейных алгебраических уравнений (6.7):
найдем из системы линейных алгебраических уравнений (6.7):
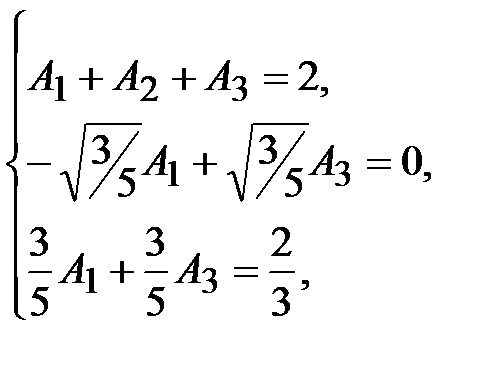
тогда 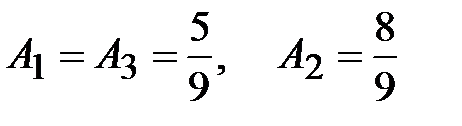 .
.
Следовательно, для любой функции 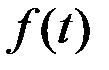 квадратурная формула Гаусса с тремя точками запишется следующим образом:
квадратурная формула Гаусса с тремя точками запишется следующим образом:
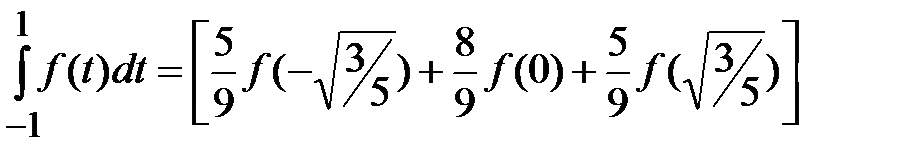 .
.
Для вычисления общего интеграла 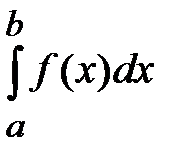 используется замена переменной
используется замена переменной 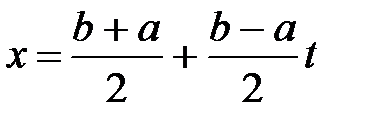 . (6.8)
. (6.8)
Получим
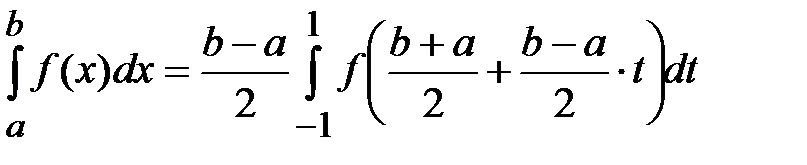 .
.
Применяя к последнему интегралу квадратурную формулу Гаусса, получим
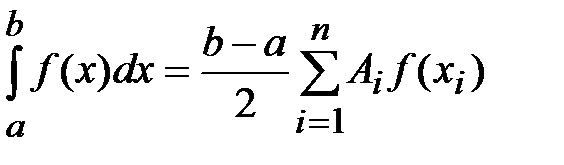 , (6.9)
, (6.9)
где 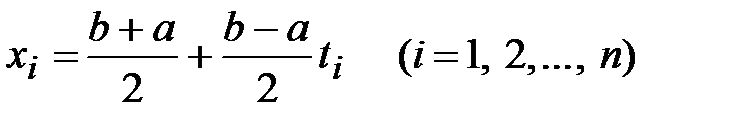 ;
; 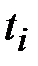 - нули полинома Лежандра
- нули полинома Лежандра 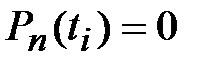 .
.
 2015-04-20
2015-04-20 687
687








