Метод трапеций

Заменяя функцию 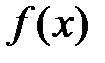на отрезке 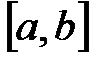ее линейной интерполяцией по точкам 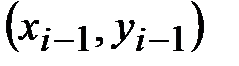и 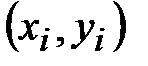, получим непрерывную кусочно-линейную функцию

, .

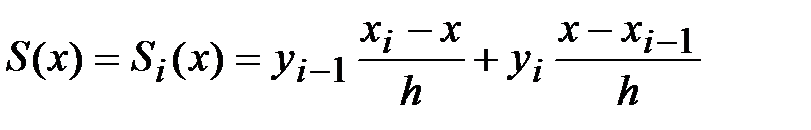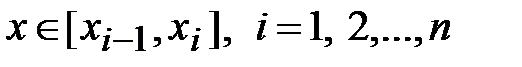Интегрируя полученную функцию на отрезке 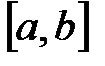, получаем формулу трапеций:

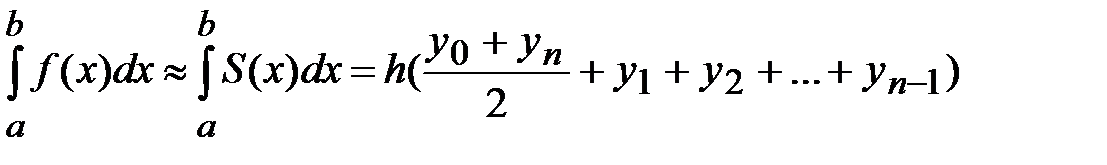. (6.1)

Метод прямоугольников

Если на каждой части 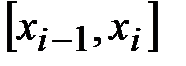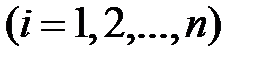деления отрезка 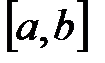функцию 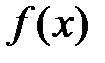заменить функцией, принимающей постоянное значение, равное значению 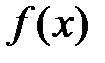в срединной точке 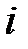-й части 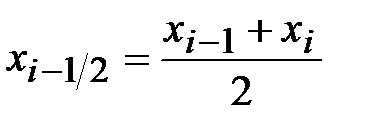, то функция будет иметь ступенчатый вид:

.

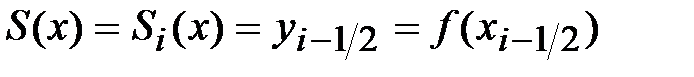Интегрируя 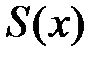на отрезке 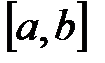, получаем квадратурную формулу прямоугольников:

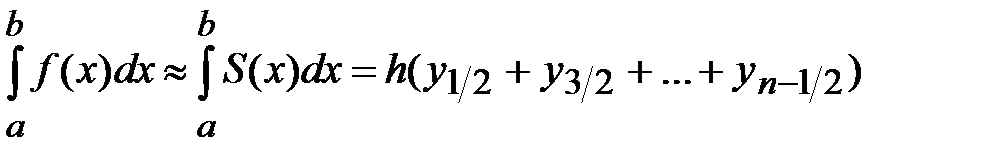. (6.2)