Двойственная задача линейного программирования

Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой. Связь исходной и двойственной задач заключается в том, что решение одной из них может быть получено из решения другой.

Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции

F = C₁X₁ + C₂X₂+…+C_nX_n (1)

при условиях

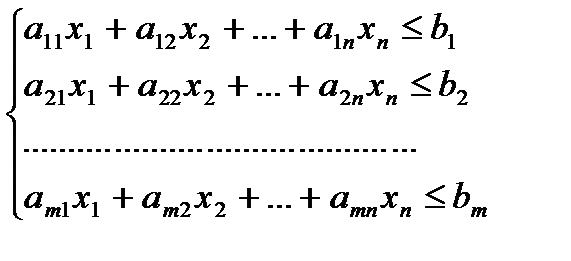(2)

x_j≥0 (j=1,n) (3)

Задача, состоящая в нахождении минимального значения функции

F*=b₁y₁+b₂y₂+…+b_my_m (4.)

при условиях

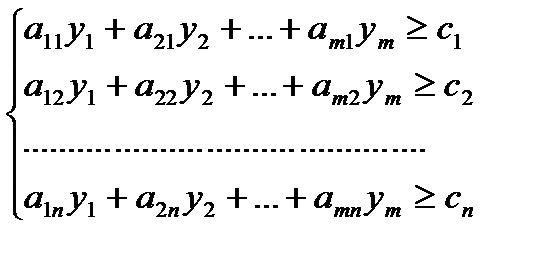(5)

y_i≥0 (i=1,m) (6)

называется двойственной задачей по отношению к задаче (1) – (3)..

Задачи (1) – (3) и (4) – (6) образуют пару задач, называемую в линейном программировании двойственной парой.

Сравнивая две сформулированные задачи, видим, что двойственная задача по отношению к исходной составляется согласно следующим правилам:

1. Целевая функция исходной задача задается на max, а целевая функция двойственной задачи на min.

2. Матрица:

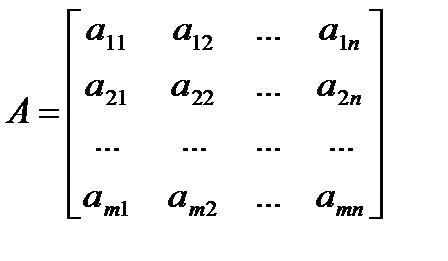
составленная из коэффициентов при неизвестных в система ограничений (2) исходной задачи и аналогичная матрица

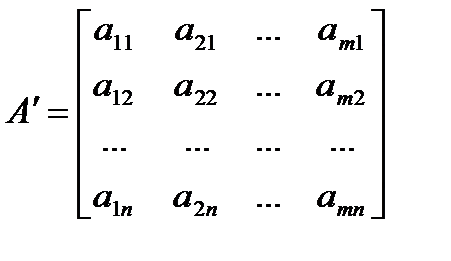
в двойственной задаче получаются друг из друга транспонированием(т.е. заменой строк столбцами, а столбцов – строками).

3. Число переменных в двойственной задаче равно числу соотношений в системе (2) исходной задачи, а число ограничений в системе(5) двойственной задачи равно числу переменных в исходной задаче.

4. Коэффициентами при неизвестных целевой функции двойственной задачи являются свободные члены системы (2) исходной задачи, а правыми частями в системе ограничений двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи.

5. Если переменная x_j исходной задачи может принимать лишь положительные значения, то j-тое условие в системе (5) двойственной задачи является неравенством вида «≥». Если же переменная x_j может принимать как положительные так и отрицательные значения, то j-тое соотношение в системе (5) является уравнением.

6. Если i-е соотношение в системе (2) исходной задачи является неравенством, то i-тая переменная двойственной задачи y_i≥0. В противном случае переменная y_i может принимать как положительные так и отрицательные значения.

Двойственные пары задач обычно подразделяются на симметричные и несимметричные.

В симметричной паре двойственной задачи ограничения вида (2) исходной задачи и соотношения (5) двойственной задачи являются неравенствами вида «≤», т.е переменные обеих задач могут принимать только неотрицательные значения.