Решение двойственной задачи

Решение двойственной задачи можно найти из конечной (оптимальной) симплекс-таблицы прямой задачи линейного программирования.

Если исходную прямую задачу линейного программирования представить в виде F=CX, AX£B, где [A]=[a_ij] – матрица коэффициентов системы, тогда в исходной симплекс-таблице она имеет вид

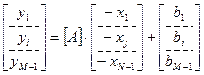, (6.11)

и строка целевой функции будет

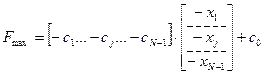. (6.12)

Для двойственной задачи Ф_min=B^TY, A^TY³C^T, Y³0

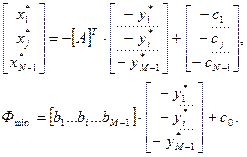
(6.13)

(6.14)

Дополнительные переменные y_i для ограничений прямой задачи формально играют роль переменных с обратным знаком двойственной задачи y_i^*.

Дополнительные переменные двойственной задачи 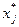могут рассматриваться как переменные с обратным знаком прямой задачи x_j.

Решение прямой задачи для любой S -итерации может быть записано с помощью матрицы перехода [P_s] в виде

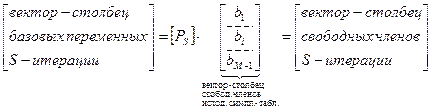
Матрица перехода для исходной симплекс-таблицы [P₀] (т.е. нулевой итерации) является единичной диагональной матрицей размерностью

(M-1)´(M-1) для прямой задачи и (N-1)´(N-1) для двойственной задачи:

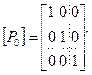
Столбцы матрицы соответствуют дополнительным элементам 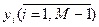прямой задачи или 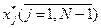для двойственной задачи и располагаются в прямом порядке y₁,y₂,…,y_i,…,y_M-1 или .

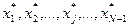Если дополнительные переменные y_i или 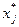прямой и двойственной задач на данной S- итерации являются базисными, то соответствующие им столбцы матрицы P_S состоят из нулей во всех строчках за исключением одной, в которой присутствует единица. Номера этих строк совпадают с номерами строк, в которых находится эта переменная в столбце базисных переменных. Столбцы матрицы перехода P_S для дополнительных переменных y_i ( 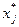), которые для рассматриваемой итерации оказались в числе свободных, соответствуют коэффициентам симплекс-таблицы на этой итерации.

Так, матрица перехода для S- итерации будет

_.

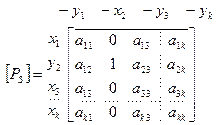Обозначим [ P ]– матрицу перехода конечной симплекс-таблицы, тогда можно записать в матричном виде решение прямой задачи следующим образом:

_.

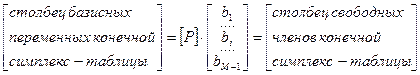Аналогично последняя симплекс-таблица двойственной задачи может быть представлена в виде

_.

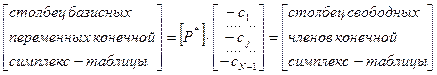Из (6.11) и (6.13) следует, что матрица системы двойственной задачи эквивалентна транспонированной матрице прямой задачи, взятой с обратным знаком, что справедливо и для матрицы конечной симплекс-таблицы.

Это можно проиллюстрировать на конкретном примере. Допустим, организуется производство трех видов изделий A, B, C в количестве x₁, x₂, x₃ соответственно из имеющихся запасов сырья b₁, b₂, b₃. При этом на производство единицы j-го изделия затрачивается a_ij единиц i-го вида сырья. Требуется максимизировать доход, если цены на единицу каждого изделия составляют соответственно с₁, с₂, с₃.

Таким образом, для определения оптимального плана производства нужно решить задачу, состоящую в максимизации целевой функции:

,

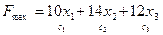при следующих ограничениях:

y1 y2 y3

4 x1 +2 x2 + x3 £180, b1 =180, 3 x1 + x2 +3 x3 £210, b2 =210, x1 +2 x2 +5 x3 £244, b3 =244, x1, x2, x3 ³ 0.

(6.15)

Конечная симплекс-таблица имеет вид

	-x1	-y1	-y3	bi
x2	19/8	5/8	-1/8
y2	23/8	1/8	-5/8
x3	-3/4	-1/4	-1/4
F	57/4	23/4	5/4

При этом матрица перехода конечной симплекс-таблицы прямой задачи будет

.

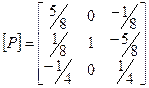Как видно из симплекс-таблицы, решение прямой задачи равно x₁ =0, x₂ =82, x₃ =16,, F_max =1340.

Кроме того, полезно запомнить значения вспомогательных переменных y₁ = y₂ =0, y₂ =80.

Двойственная задача запишется следующим образом: найти минимум функции

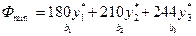
при ограничениях:

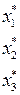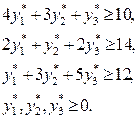с1 = 10, с2 = 14, с3 = 12.

(6.16)

Конечную симплекс-таблицу двойственной задачи исходя из конечной симплекс-таблицы прямой задачи можно записать в виде

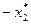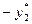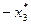				cj
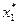	-19/8	-23/8	3/4	57/4
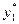	-5/8	-1/8	1/4	23/4
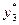	1/8	5/8	-1/4	5/4
Ф				-1340

А матрица перехода для двойственной задачи будет

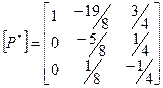
Решение двойственной задачи составляет: ,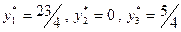

Ф= –1340.

При этом полезно знать значения вспомогательных переменных 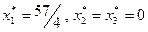для последующего исследования решения задачи.