Контрольная работа по дисциплине «Математика»
1. Вычислить неопределенные интегралы.
| № вар | Задания |
1) 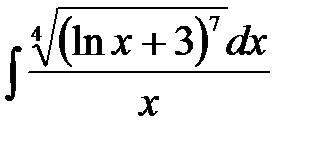 ; 2) ; 2) 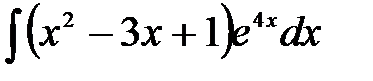 ; 3) ; 3) 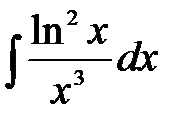 ; 4) ; 4) 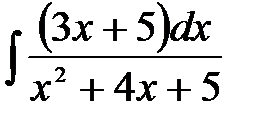 ;
5) ;
5) 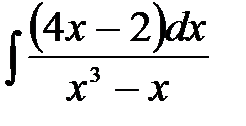 ; 6) ; 6) 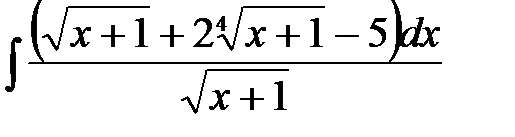 ; 7) ; 7) 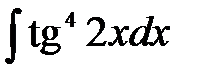 ; ;
| |
1) 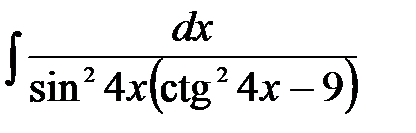 ; 2) ; 2) 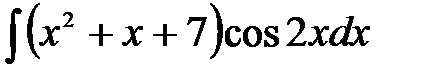 ; 3) ; 3) 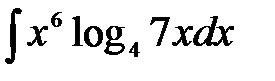 ;
4) ;
4) 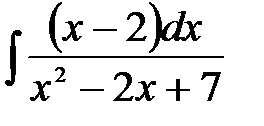 ; 5) ; 5) 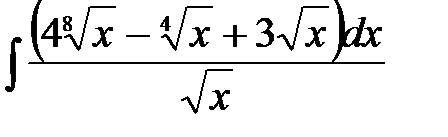 ; 6) ; 6) 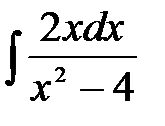 ;
7) ;
7) 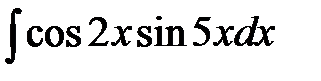 ; ;
| |
1) 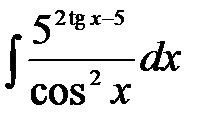 ; 2) ; 2) 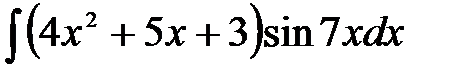 ; 3) ; 3) 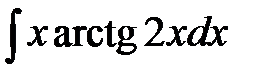 ;
4) ;
4) 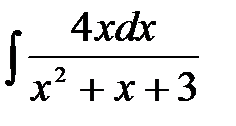 ; 5) ; 5) 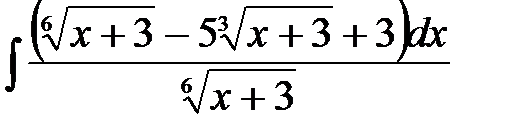 ; 6) ; 6) 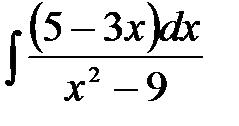 ;
7) ;
7) 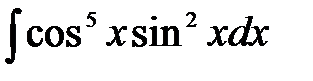 ; ;
| |
1) 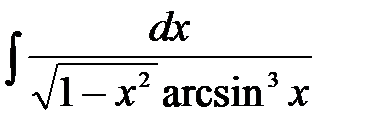 ; 2) ; 2) 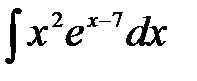 ; 3) ; 3) 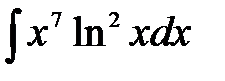 ; 4) ; 4) 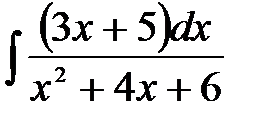 ;
5) ;
5) 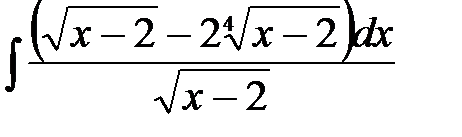 ; 6) ; 6) 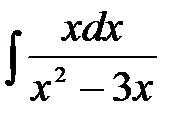 ; 7) ; 7) 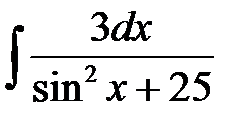 ; ;
| |
1) 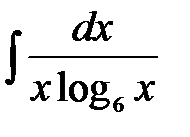 ; 2) ; 2) 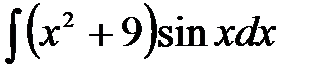 ; 3) ; 3) 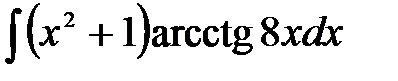 ;
4) ;
4) 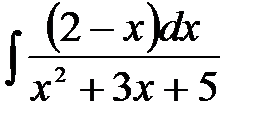 ; 5) ; 5) 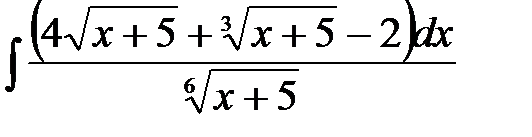 ; 6) ; 6) 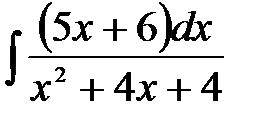 ;
7) ;
7) 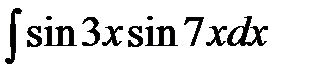 ; ;
| |
1) 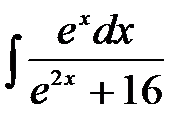 ; 2) ; 2) 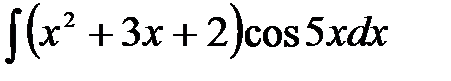 ; 3) ; 3) 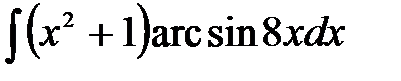 ;
4) ;
4) 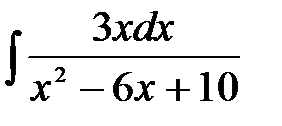 ; 5) ; 5) 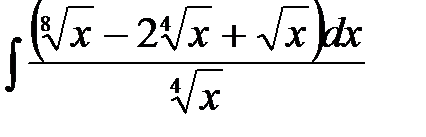 ; 6) ; 6) 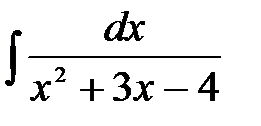 ;
7) ;
7) 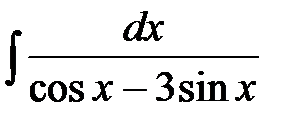 ; ;
| |
1) 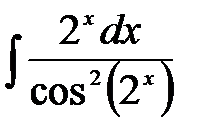 ; 2) ; 2) 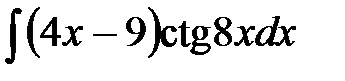 ; 3) ; 3) 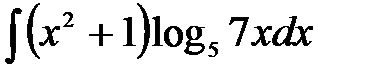 ;
4) ;
4) 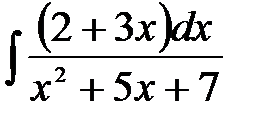 ; 5) ; 5) 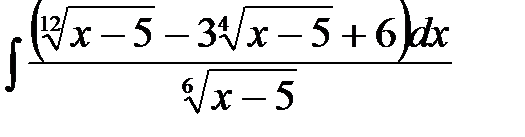 ; 6) ; 6) 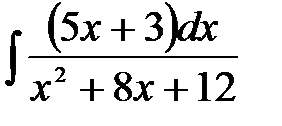 ;
7) ;
7) 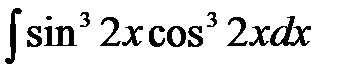 ; ;
| |
1) 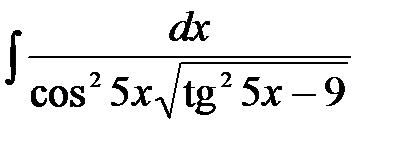 ; 2) ; 2) 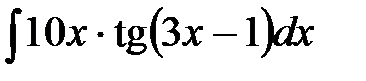 ; 3) ; 3) 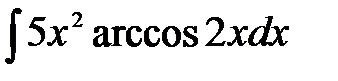 ;
4) ;
4) 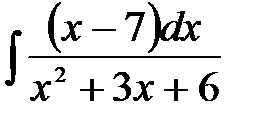 ; 5) ; 5) 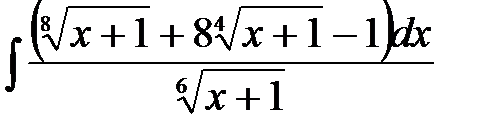 ; 6) ; 6) 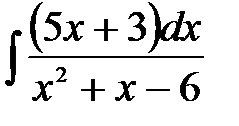 ;
7) ;
7) 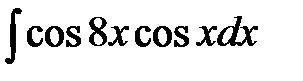 ; ;
| |
1) 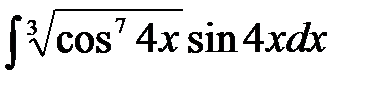 ; 2) ; 2) 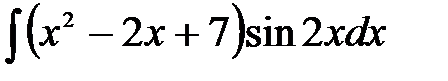 ;
3) ;
3) 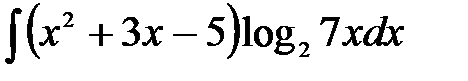 ; 4) ; 4) 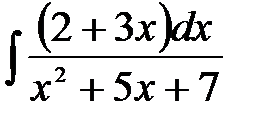 ; 5) ; 5) 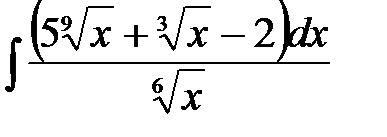 ;
6) ;
6) 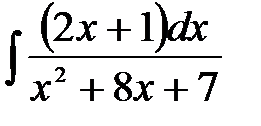 ; 7) ; 7) 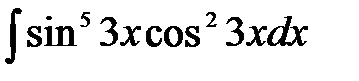 ; ;
| |
1) 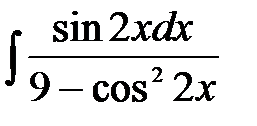 ; 2) ; 2) 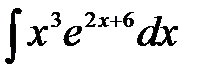 ; 3) ; 3) 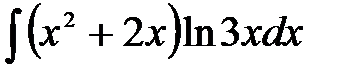 ; 4) ; 4) 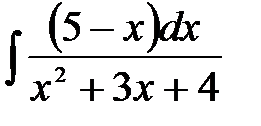 ;
5) ;
5) 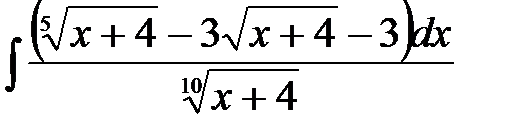 ; 6) ; 6) 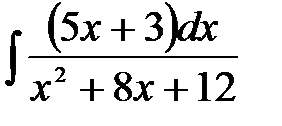 ; 7) ; 7) 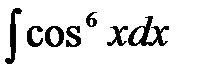 ; ;
| |
1) 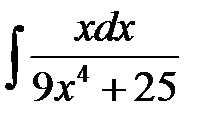 ; 2) ; 2) 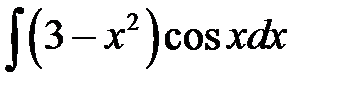 ; 3) ; 3) 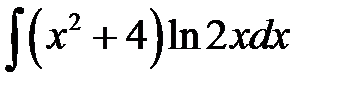 ; 4) ; 4) 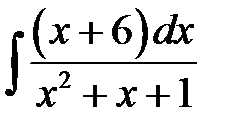 ;
5) ;
5) 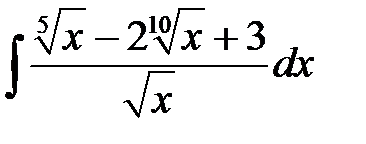 ; 6) ; 6) 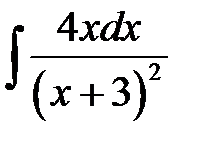 ; 7) ; 7) 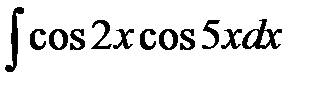 ; ;
| |
1) 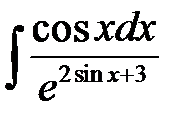 ; 2) ; 2) 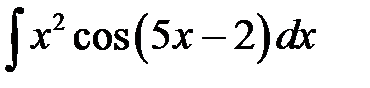 ; 3) ; 3) 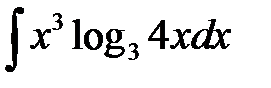 ; 4) ; 4) 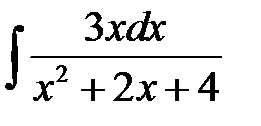 ;
5) ;
5) 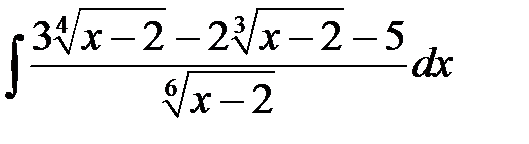 ; 6) ; 6) 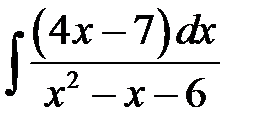 ; 7) ; 7) 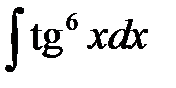 ; ;
| |
1) 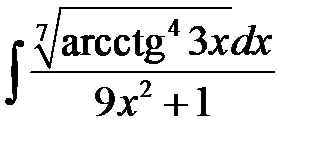 ; 2) ; 2) 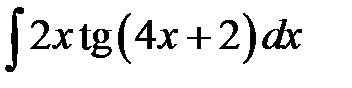 ; 3) ; 3) 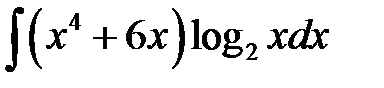 ;
4) ;
4) 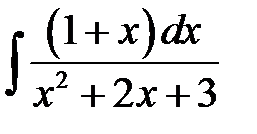 ; 5) ; 5) 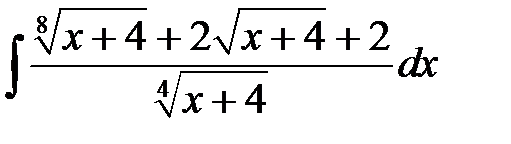 ; 6) ; 6) 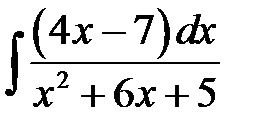 ;
7) ;
7) 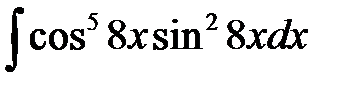 ; ;
| |
1) 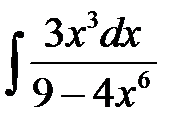 ; 2) ; 2) 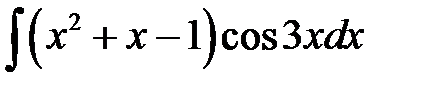 ; 3) ; 3) 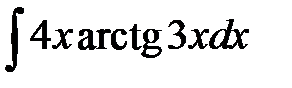 ;
4) ;
4) 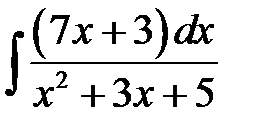 ; 5) ; 5) 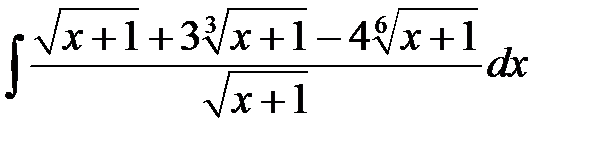 ; 6) ; 6) 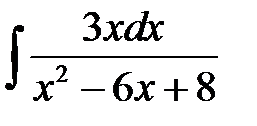 ;
7) ;
7) 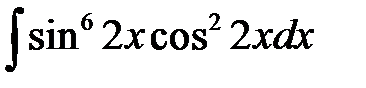 ; ;
| |
1) 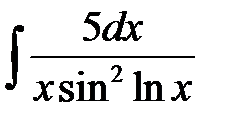 ; 2) ; 2) 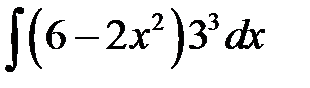 ; 3) ; 3) 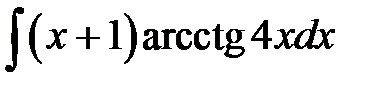 ;
4) ;
4) 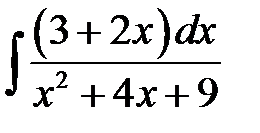 ; 5) ; 5) 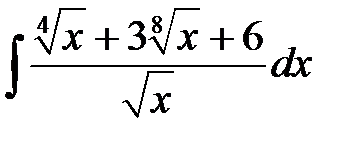 ; 6) ; 6) 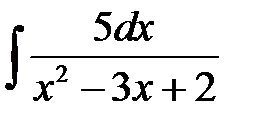 ; 7) ; 7) 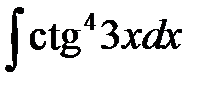 ; ;
| |
1) 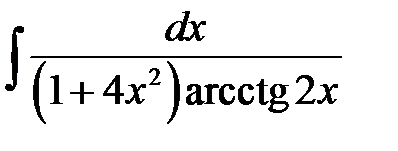 ; 2) ; 2) 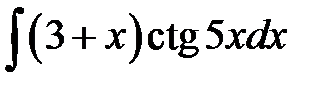 ; 3) ; 3) 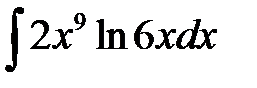 ;
4) ;
4) 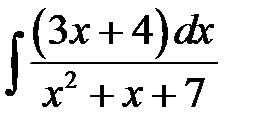 ; 5) ; 5) 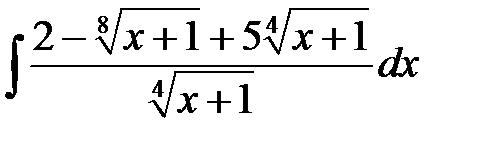 ; 6) ; 6) 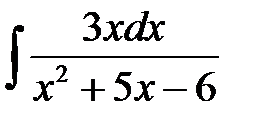 ;
7) ;
7) 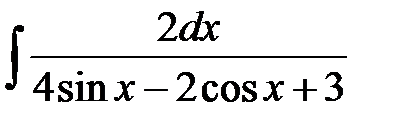 ; ;
| |
1) 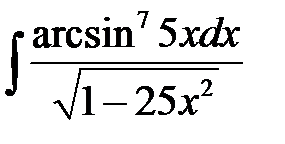 ; 2) ; 2) 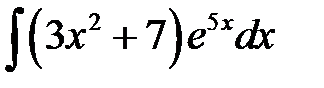 ; 3) ; 3) 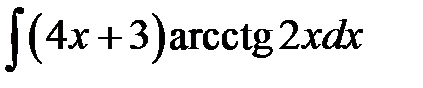 ;
4) ;
4) 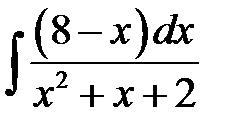 ; 5) ; 5) 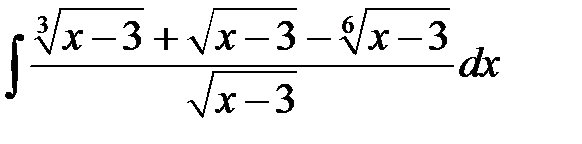 ; 6) ; 6) 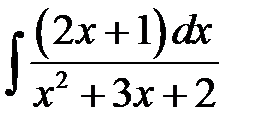 ;
7) ;
7) 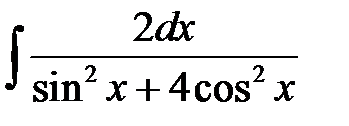 ; ;
| |
1) 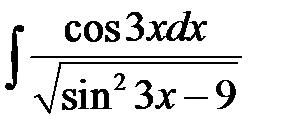 ; 2) ; 2) 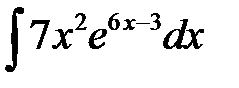 ; 3) ; 3) 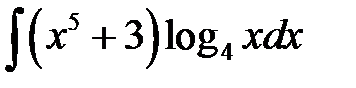 ; 4) ; 4) 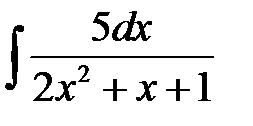 ;
5) ;
5) 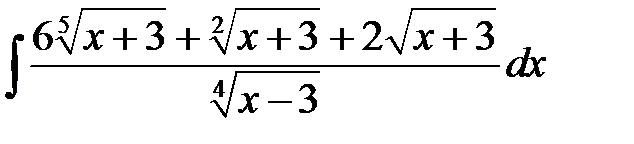 ; 6) ; 6) 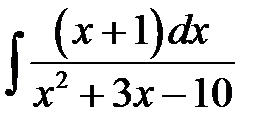 ; 7) ; 7) 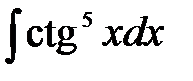 ; ;
| |
1) 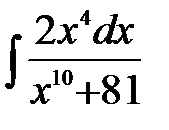 ; 2) ; 2) 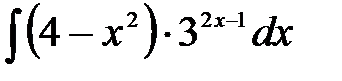 ; 3) ; 3) 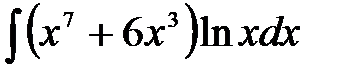 ; 4) ; 4) 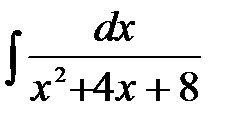 ;
5) ;
5) 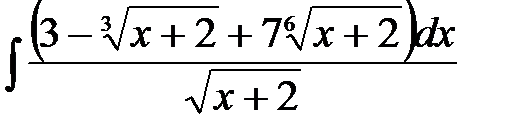 ; 6) ; 6) 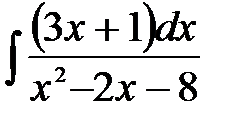 ; 7) ; 7) 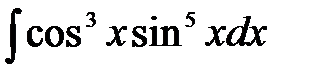 ; ;
| |
1) 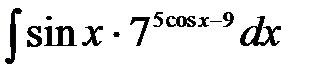 ; 2) ; 2) 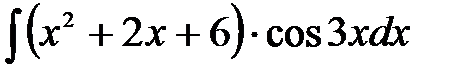 ; 3) ; 3) 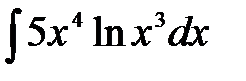 ;
4) ;
4) 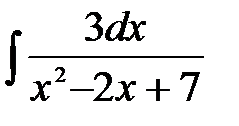 ; 5) ; 5) 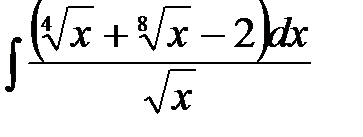 ; 6) ; 6) 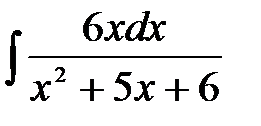 ; 7) ; 7) 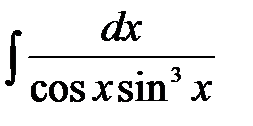 ; ;
| |
1) 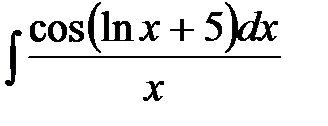 ; 2) ; 2) 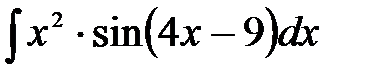 ; 3) ; 3) 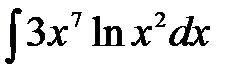 ;
4) ;
4) 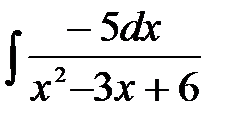 ; 5) ; 5) 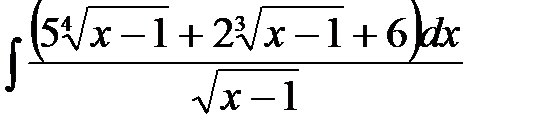 ; 6) ; 6) 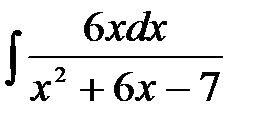 ;
7) ;
7) 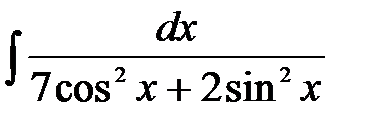 ; ;
| |
1) 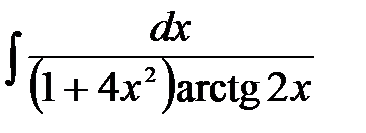 ; 2) ; 2) 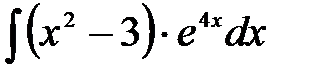 ; 3) ; 3) 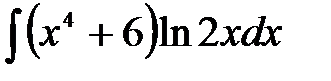 ;
4) ;
4) 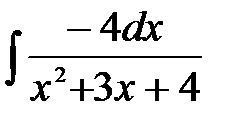 ; 5) ; 5) 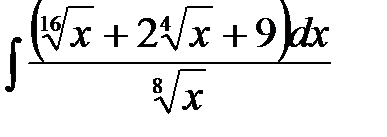 ; 6) ; 6) 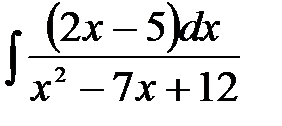 ;
7) ;
7) 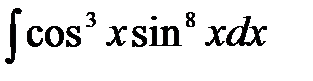 ; ;
| |
1) 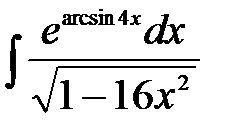 ; 2) ; 2) 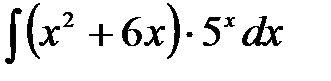 ; 3) ; 3) 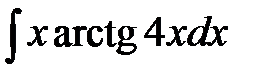 ; 4) ; 4) 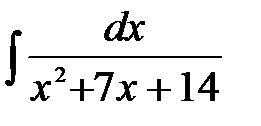 ;
5) ;
5) 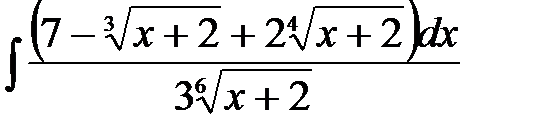 ; 6) ; 6) 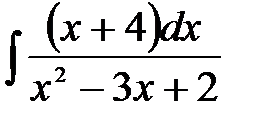 ; 7) ; 7) 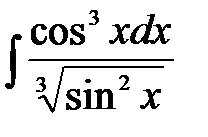 ; ;
| |
1) 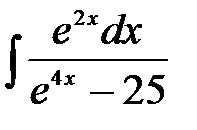 ; 2) ; 2) 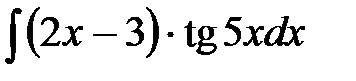 ; 3) ; 3)  ;
4) ;
4) 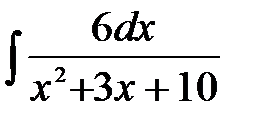 ; 5) ; 5) 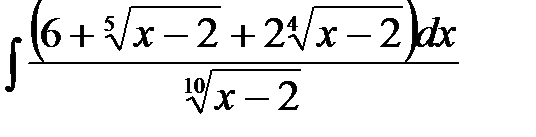 ; 6) ; 6) 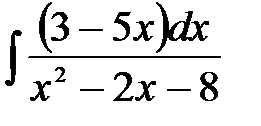 ;
7) ;
7) 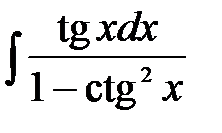 ; ;
| |
1) 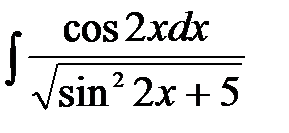 ; 2) ; 2) 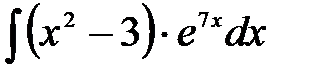 ; 3) ; 3) 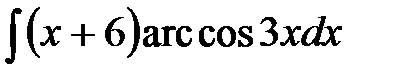 ;
4) ;
4) 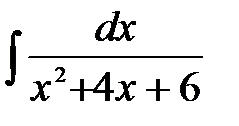 ; 5) ; 5) 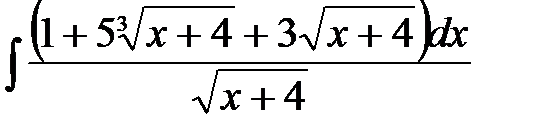 ; 6) ; 6) 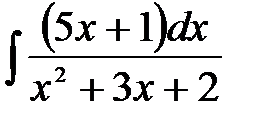 ;
7) ;
7) 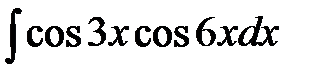 ; ;
| |
1) 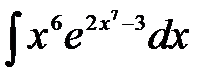 ; 2) ; 2) 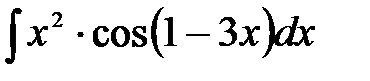 ; 3) ; 3) 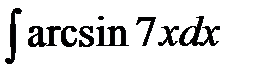 ; 4) ; 4) 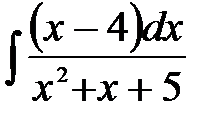 ;
5) ;
5) 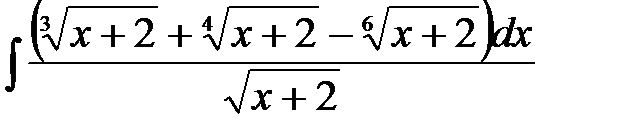 ; 6) ; 6) 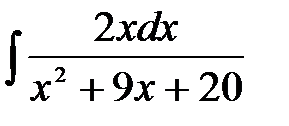 ; 7) ; 7) 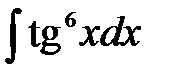 ; ;
| |
1) 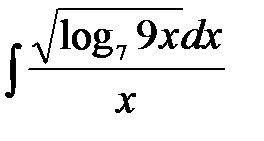 ; 2) ; 2) 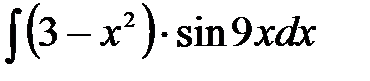 ; 3) ; 3) 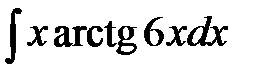 ; 4) ; 4) 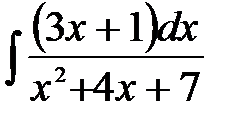 ;
5) ;
5) 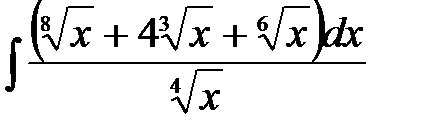 ; 6) ; 6) 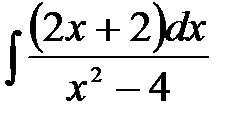 ; 7) ; 7) 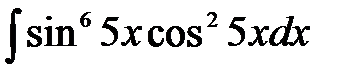 ; ;
| |
1) 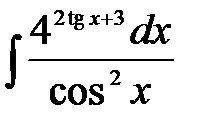 ; 2) ; 2) 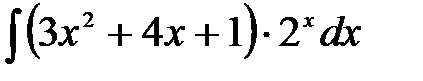 ; 3) ; 3) 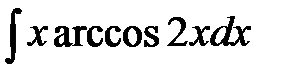 ;
4) ;
4) 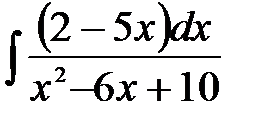 ; 5) ; 5) 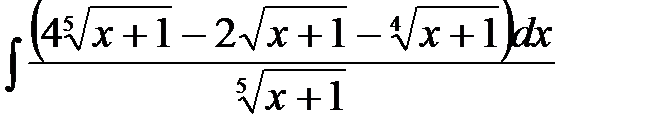 ; 6) ; 6) 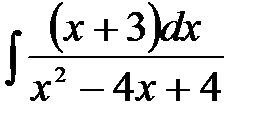 ;
7) ;
7) 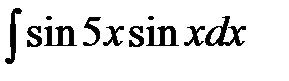 ; ;
| |
1) 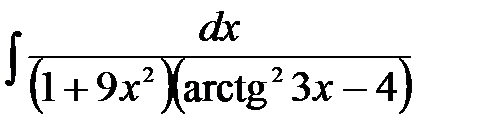 ; 2) ; 2) 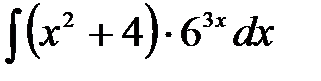 ; 3) ; 3) 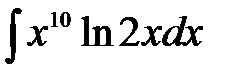 ;
4) ;
4) 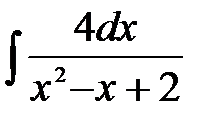 ; 5) ; 5) 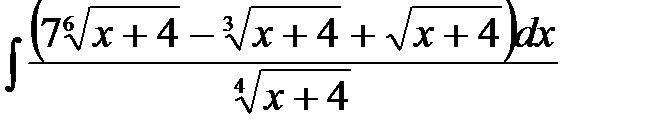 ; 6) ; 6) 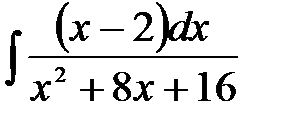 ;
7) ;
7) 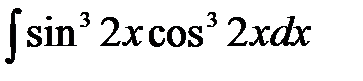 ; ;
| |
1) 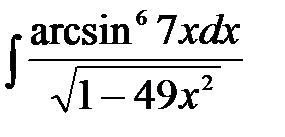 ; 2) ; 2) 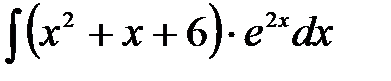 ; 3) ; 3) 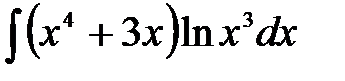 ;
4) ;
4) 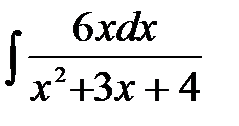 ; 5) ; 5) 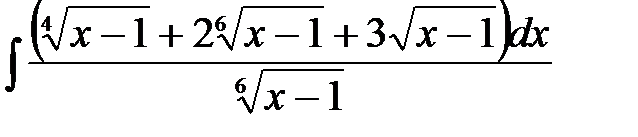 ; 6) ; 6) 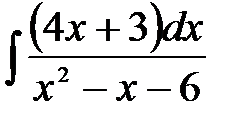 ;
7) ;
7) 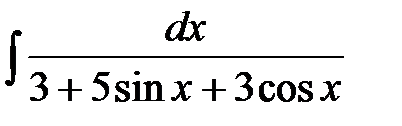 . .
|
2. С помощью определенного интеграла вычислить площадь фигуры, ограниченной указанными линиями.
| № вар | Задания | № вар | Задания |
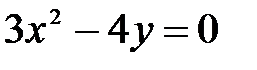 , , 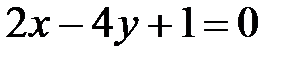
| 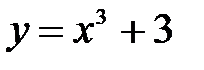 , , 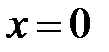 , , 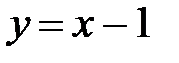 , , 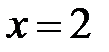
| ||
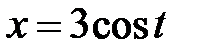 , , 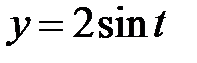
| 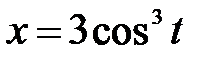 , , 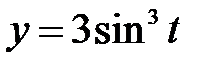
| ||
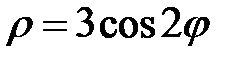
| 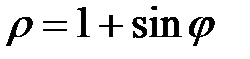
| ||
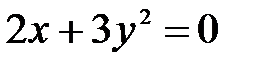 , , 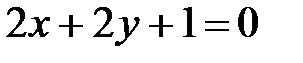
| 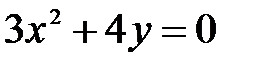 , , 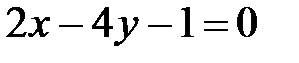
| ||
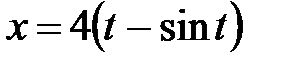 , , 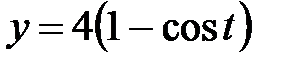
| 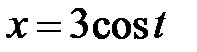 , , 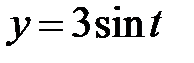
| ||
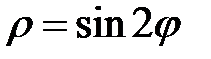
| 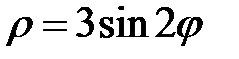
| ||
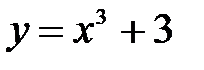 , , 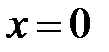 , , 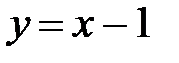 , , 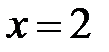
| 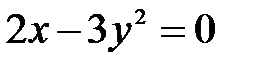 , , 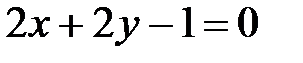
| ||
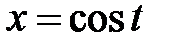 , , 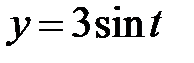
| 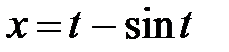 , , 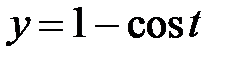
| ||
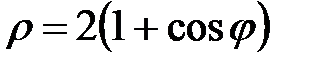
| 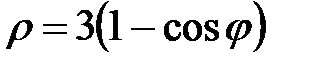
| ||
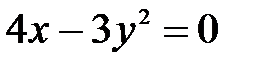 , , 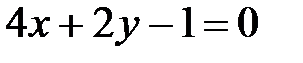
| 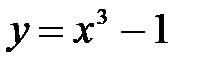 , , 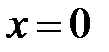 , , 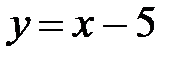 , , 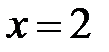
| ||
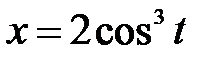 , , 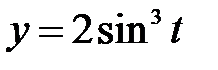
| 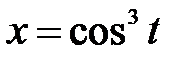 , , 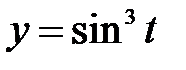
| ||
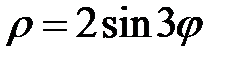
| 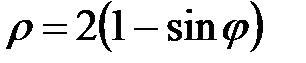
| ||
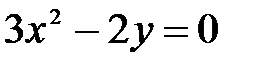 , , 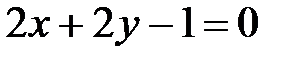
| 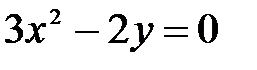 , , 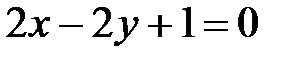
| ||
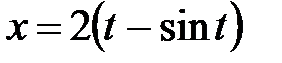 , , 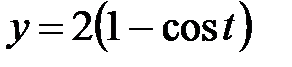
| 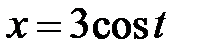 , , 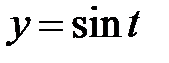
| ||
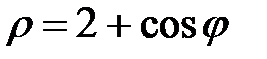
| 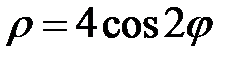
|
3. Найти общие решения (общий интеграл) дифференциальных уравнений первого порядка.
| № вар | Задания |
1) 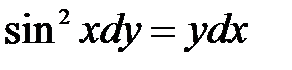 ; 2) ; 2) 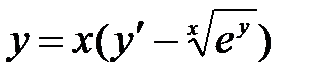 ; 3) ; 3) 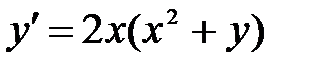 ; ;
| |
1) 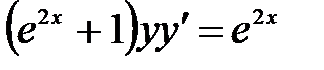 ; 2) ; 2) 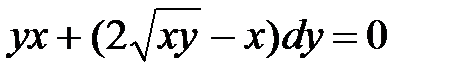 ; 3) ; 3) 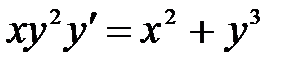 ; ;
| |
1) 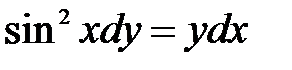 ; 2) ; 2) 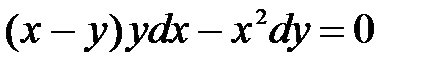 ; 3) ; 3) 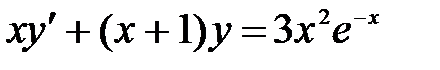 ; ;
| |
1) 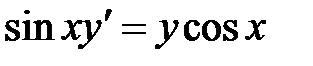 ; 2) ; 2) 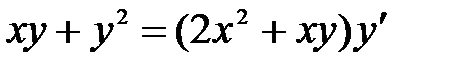 ; 3) ; 3) 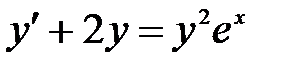 ; ;
| |
1) 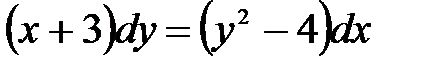 ; 2) ; 2) 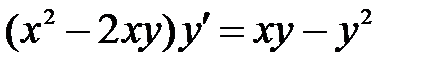 ; 3) ; 3) 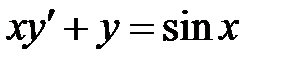 ; ;
| |
1) 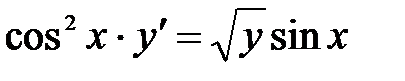 ; 2) ; 2) 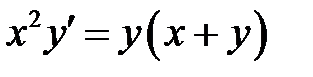 ; 3) ; 3) 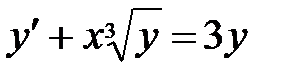 ; ;
| |
1) 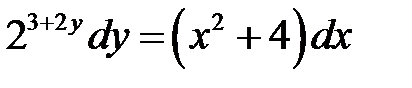 ; 2) ; 2) 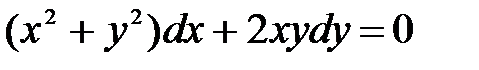 ; 3) ; 3) 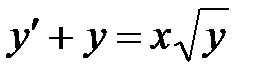 ; ;
| |
1) 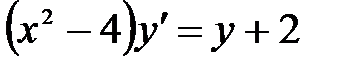 ; 2) ; 2) 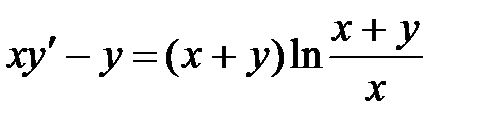 ; 3) ; 3) 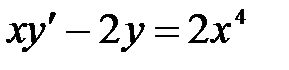 ; ;
| |
1) 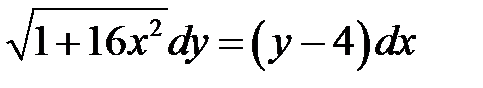 ; 2) ; 2) 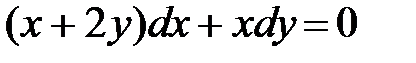 ; 3) ; 3) 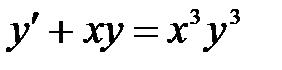 ; ;
| |
1) 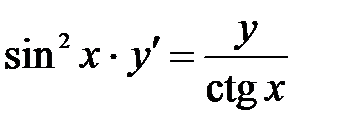 ; 2) ; 2) 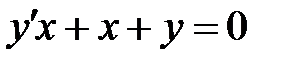 ; 3) ; 3) 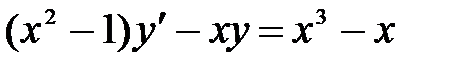 ; ;
| |
1) 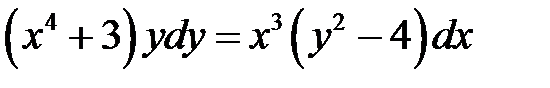 ; 2) ; 2) 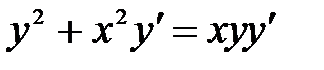 ; 3) ; 3) 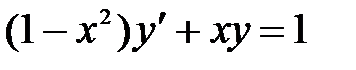
| |
1)  ; 2) ; 2) 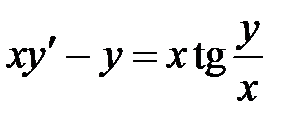 ; 3) ; 3) 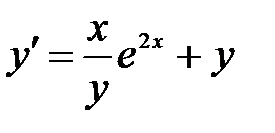 ; ;
| |
1) 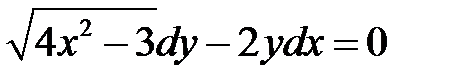 ; 2) ; 2) 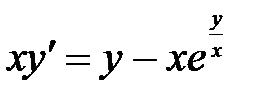 ; 3) ; 3) 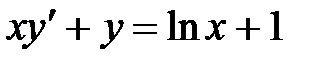 ; ;
| |
1) 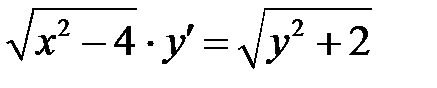 ; 2) ; 2) 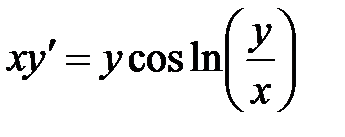 ; 3) ; 3) 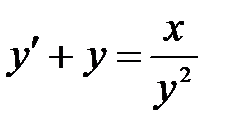 ; ;
| |
1) 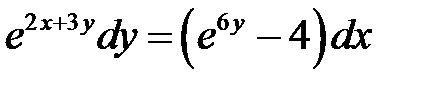 ; 2) ; 2) 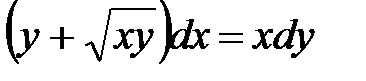 ; 3) ; 3) 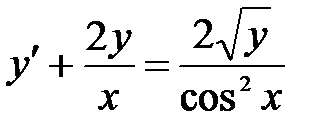 ; ;
| |
1) 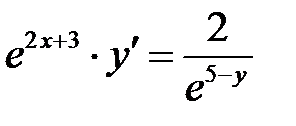 ; 2) ; 2) 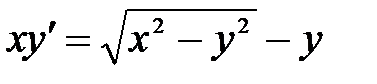 ; 3) ; 3) 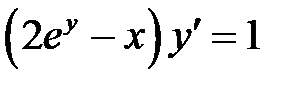 ; ;
| |
1) 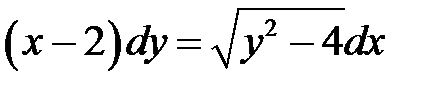 ; 2) ; 2) 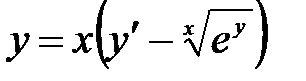 ; 3) ; 3) 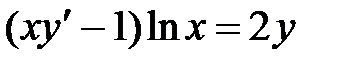 ; ;
| |
1) 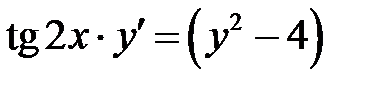 ; 2) ; 2) 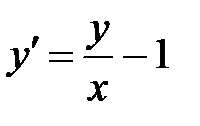 ; 3) ; 3) 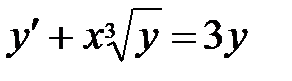 ; ;
| |
1) 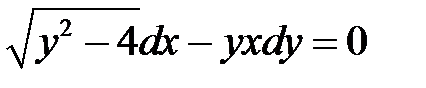 ; 2) ; 2) 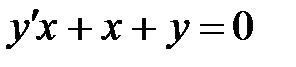 ; 3) ; 3) 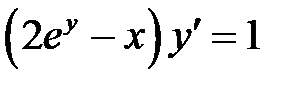 ; ;
| |
1) 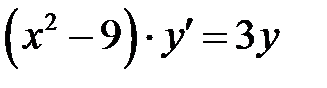 ; 2) ; 2) 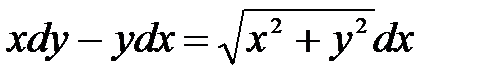 ; 3) ; 3) 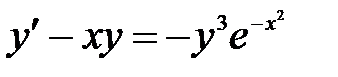 ; ;
| |
1) 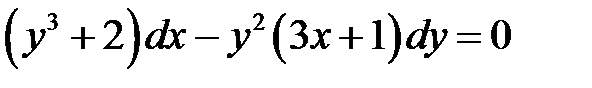 ; 2) ; 2) 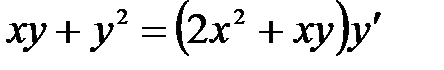 ;
3) ;
3) 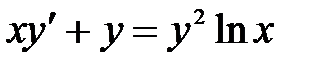 ; ;
| |
1) 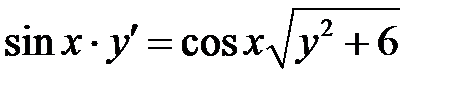 ; 2) ; 2) 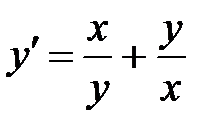 ; 3) ; 3) 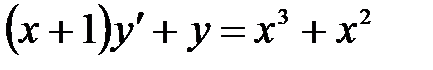 ; ;
| |
1) 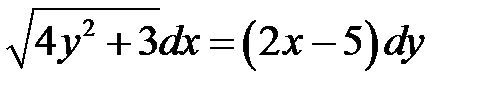 ; 2) ; 2) 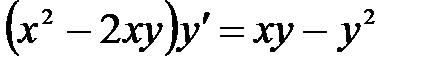 ; 3) ; 3) 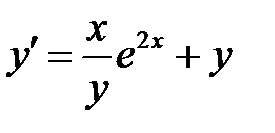 ; ;
| |
1) 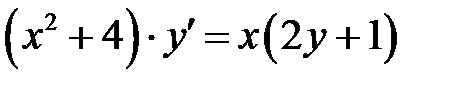 ; 2) ; 2) 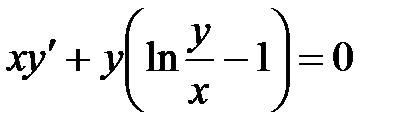 ; 3) ; 3) 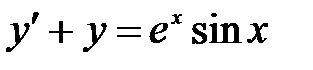 ; ;
| |
1) 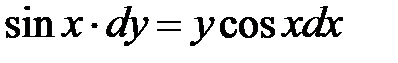 ; 2) ; 2) 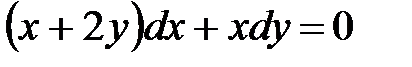 ; 3) ; 3) 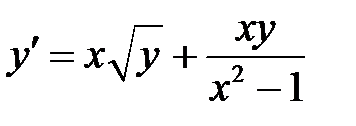 ; ;
| |
1) 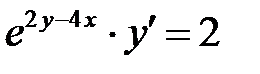 ; 2) ; 2) 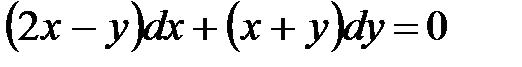 ; 3) ; 3) 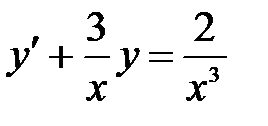 ; ;
| |
1) 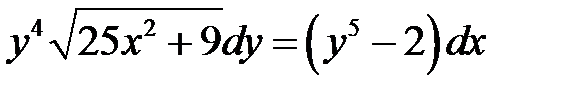 ; 2) ; 2) 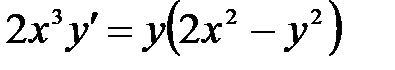 ;
3) ;
3) 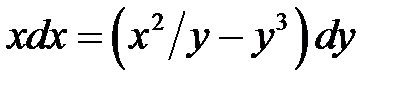 ; ;
| |
1) 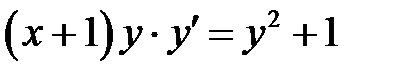 ; 2) ; 2) 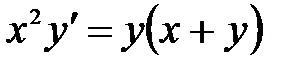 ; 3) ; 3) 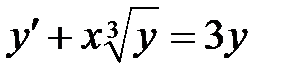 ; ;
| |
1) 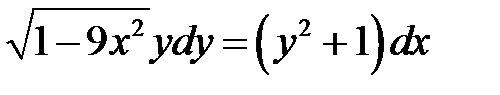 ; 2) ; 2) 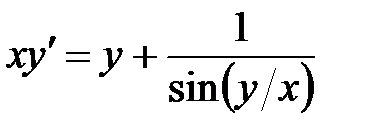 ; 3) ; 3) 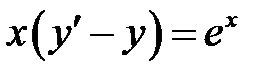 ; ;
| |
1) 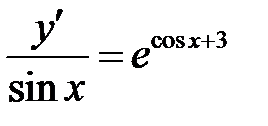 ; 2) ; 2) 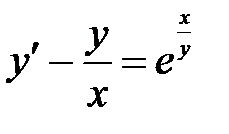 ; 3) ; 3) 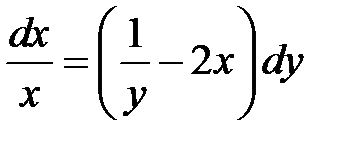 ; ;
|
4. Найти общие решения линейных неоднородных дифференциальных уравнений второго порядка.
| № вар | Задания |
1) 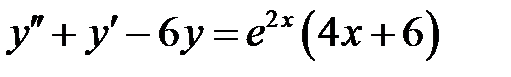 ; 2) ; 2) 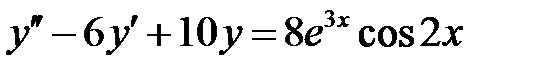 ; ;
| |
1) 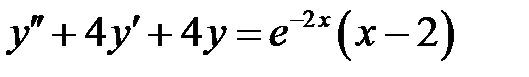 ; 2) ; 2) 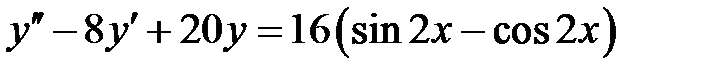 ; ;
| |
1) 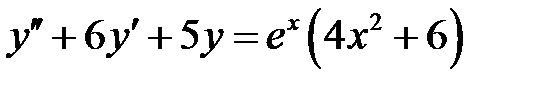 ; 2) ; 2) 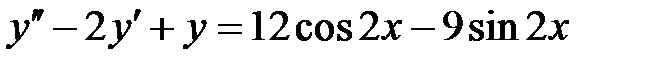 ; ;
| |
1) 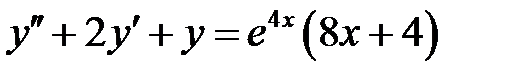 ; 2) ; 2) 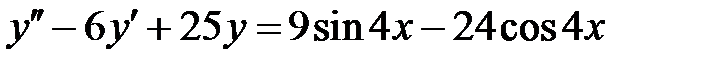 ; ;
| |
1) 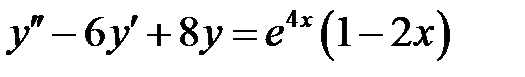 ; 2) ; 2) 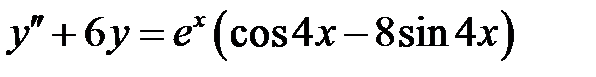 ; ;
| |
1) 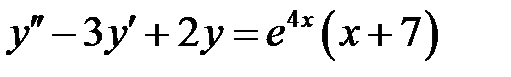 ; 2) ; 2) 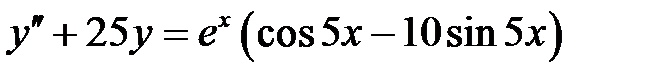 ; ;
| |
1) 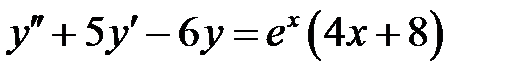 ; 2) ; 2) 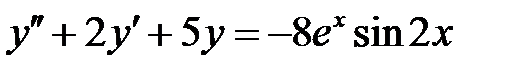 ; ;
| |
1) 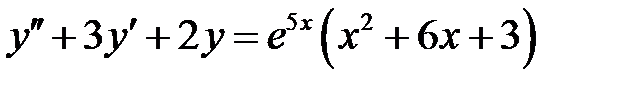 ; 2) ; 2) 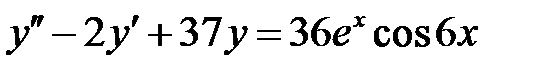 ; ;
| |
1) 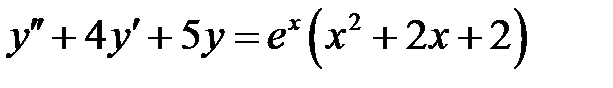 ; 2) ; 2) 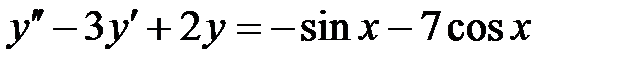 ; ;
| |
1) 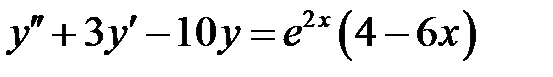 ; 2) ; 2) 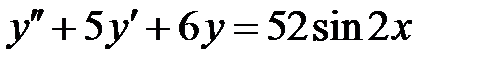 ; ;
| |
1) 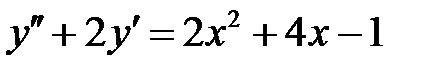 ; 2) ; 2) 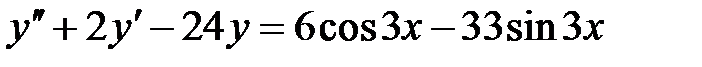 ; ;
| |
1) 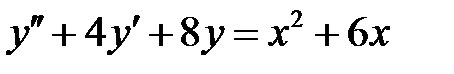 ; 2) ; 2) 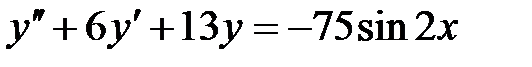 ; ;
| |
1) 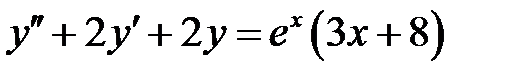 ; 2) ; 2) 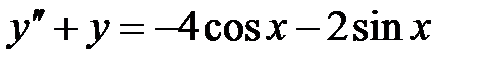 ; ;
| |
1) 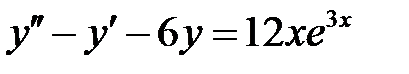 ; 2) ; 2) 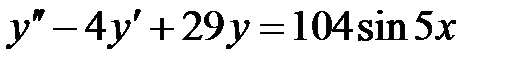 ; ;
| |
1) 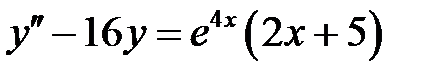 ; 2) ; 2) 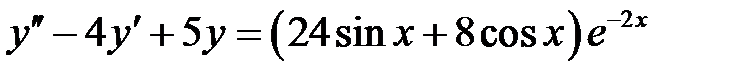 ; ;
| |
1) 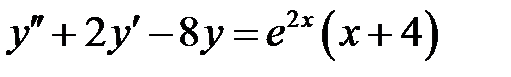 ; 2) ; 2) 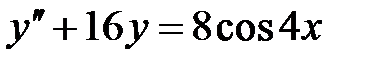 ; ;
| |
1) 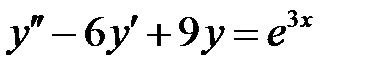 ; 2) ; 2) 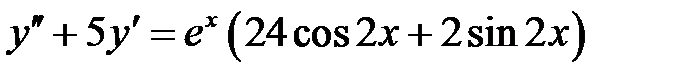 ; ;
| |
1) 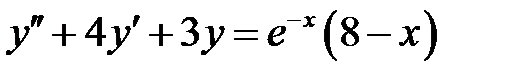 ; 2) ; 2) 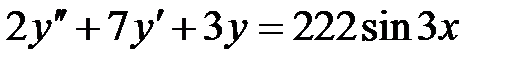 ; ;
| |
1) 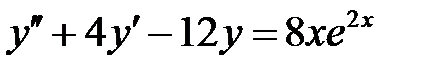 ; 2) ; 2) 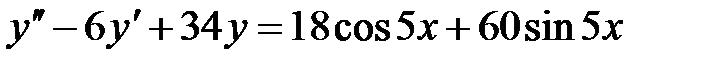 ; ;
| |
1) 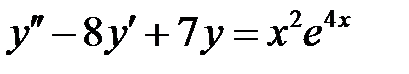 ; 2) ; 2) 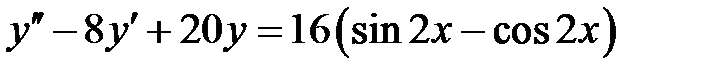 ; ;
| |
1) 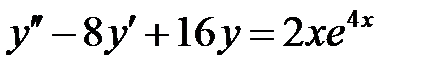 ; 2) ; 2) 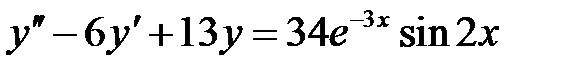 ; ;
| |
1) 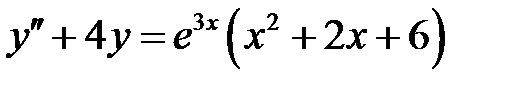 ; 2) ; 2) 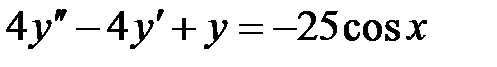 ; ;
| |
1) 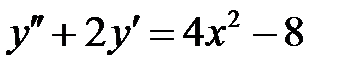 ; 2) ; 2) 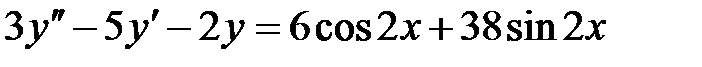 ; ;
| |
1) 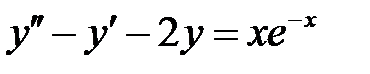 ; 2) ; 2) 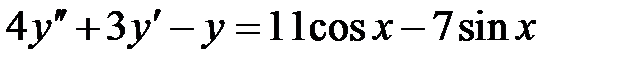 ; ;
| |
1) 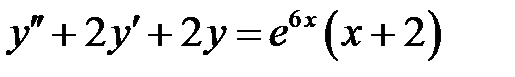 ; 2) ; 2) 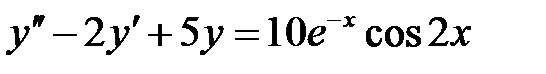 ; ;
| |
1) 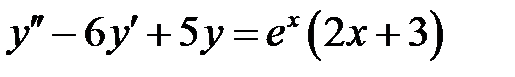 ; 2) ; 2) 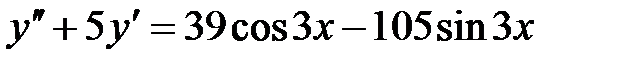 ; ;
| |
1) 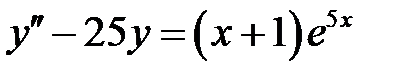 ; 2) ; 2) 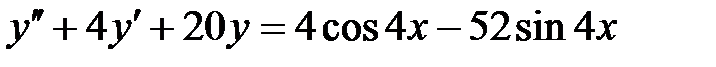 ; ;
| |
1) 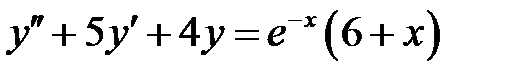 ; 2) ; 2) 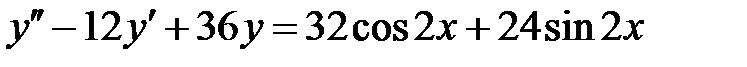 ; ;
| |
1) 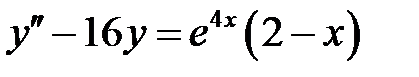 ; 2) ; 2) 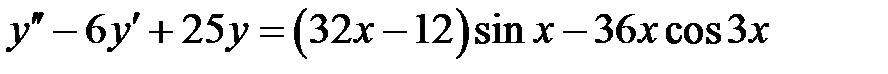 ; ;
| |
1) 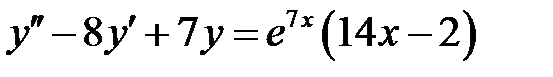 ; 2) ; 2) 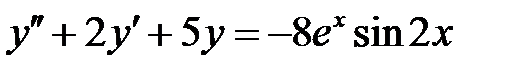 ; ;
|
5. Изменить порядок интегрирования в повторном интеграле и сделать чертеж области интегрирования.
| № вар | Задания | № вар | Задания |
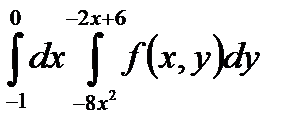
| 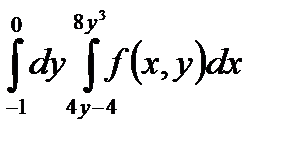
| ||
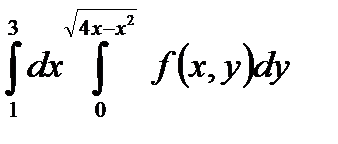
| 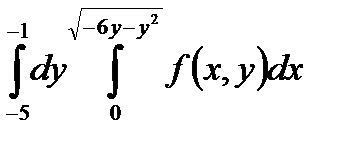
| ||
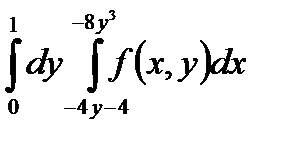
| 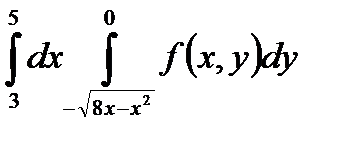
| ||
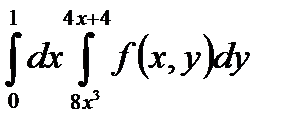
| 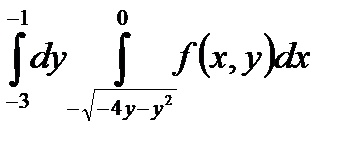
| ||
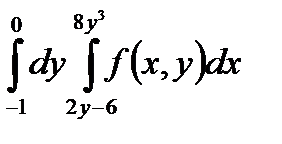
| 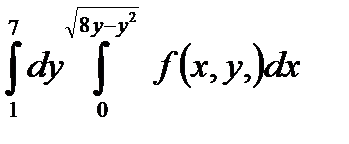
| ||
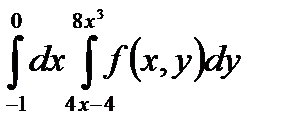
| 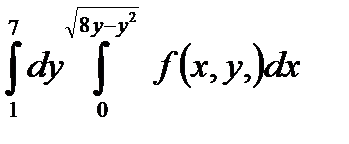
| ||
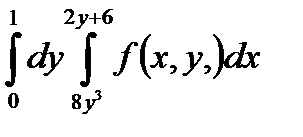
| 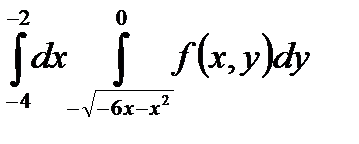
| ||
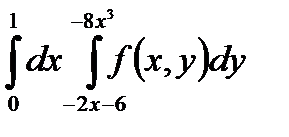
| 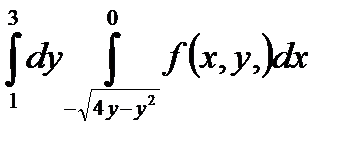
| ||
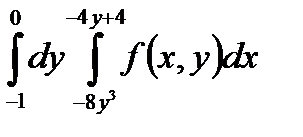
| 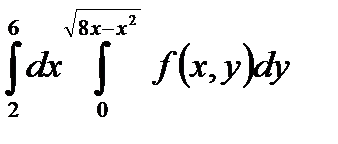
| ||
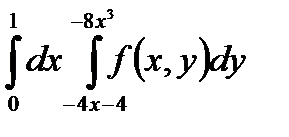
| 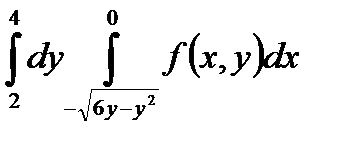
|
Представить двойной интеграл 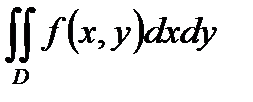 в виде повторного с внешним интегрированием по x и внешним интегрированием по y, если границы области интегрирования D ограничены кривыми с уравнениями:
в виде повторного с внешним интегрированием по x и внешним интегрированием по y, если границы области интегрирования D ограничены кривыми с уравнениями:
| № вар | Задания | № вар | Задания |
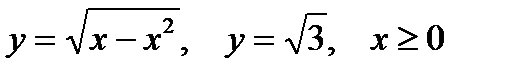
| 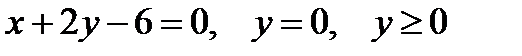
| ||
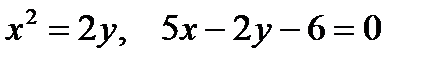
| 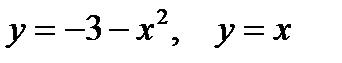
| ||
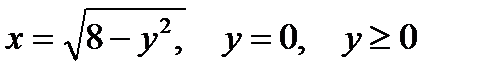
| 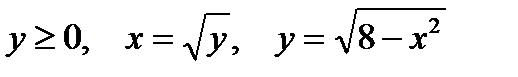
| ||
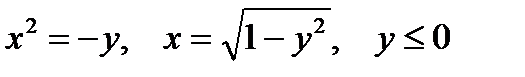
| 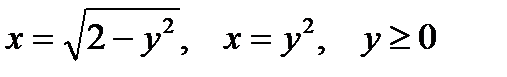
| ||
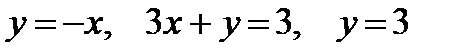
| 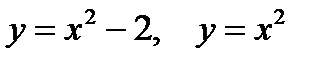
|
6. Вычислить двойные интегралы, используя полярные координаты.
| № вар | Задания |
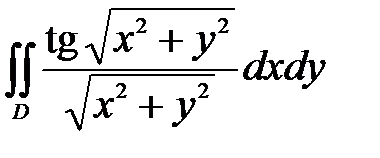 , , 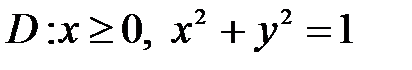
| |
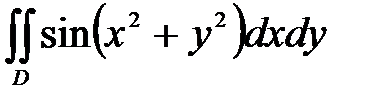 , , 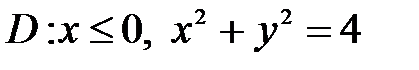
| |
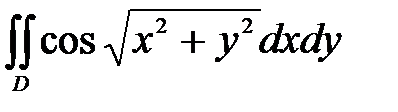 , , 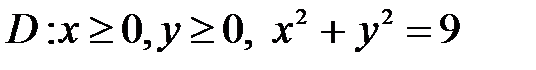
| |
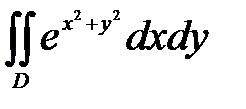 , , 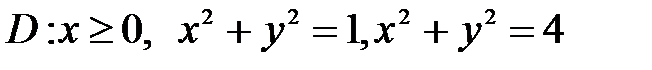
| |
 , , 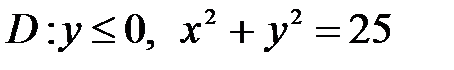
| |
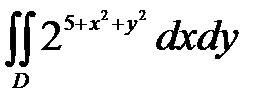 , , 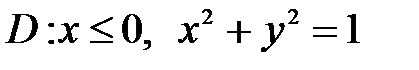
| |
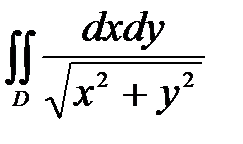 , , 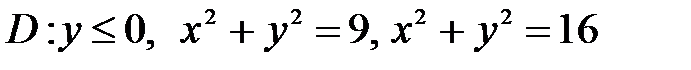
| |
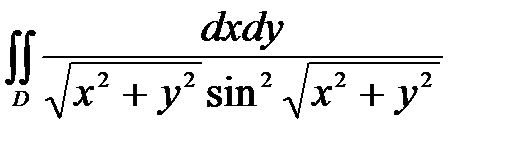 , , 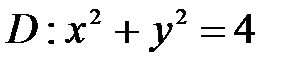
| |
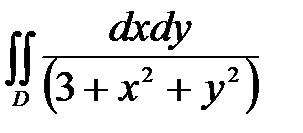 , , 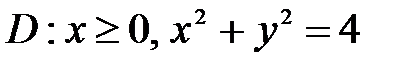
| |
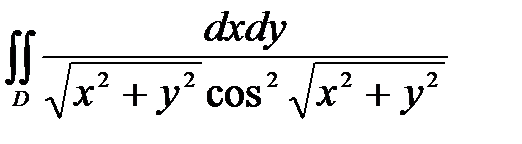 , , 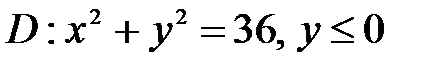
| |
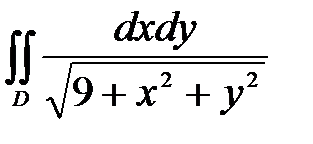 , , 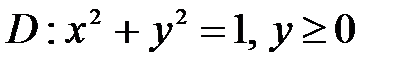
| |
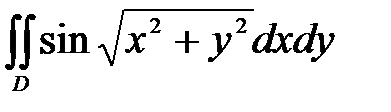 , , 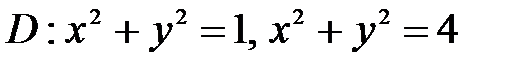
| |
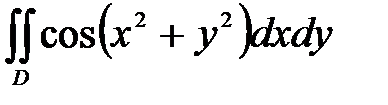 , , 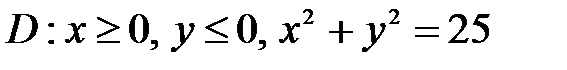
| |
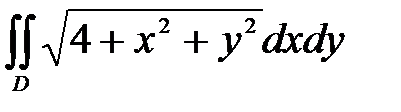 , , 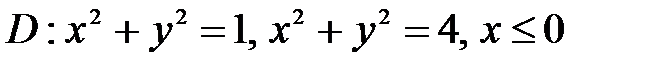
| |
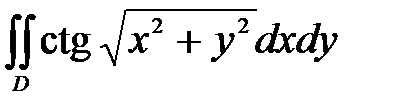 , , 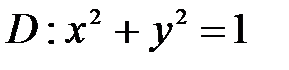
| |
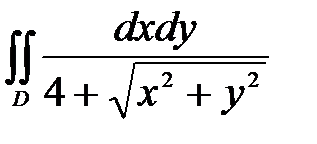 , , 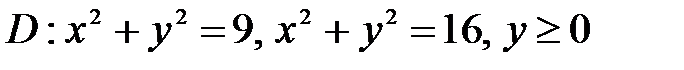
| |
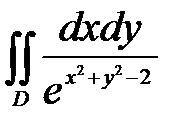 , , 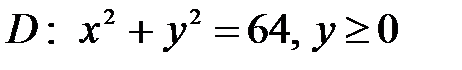
| |
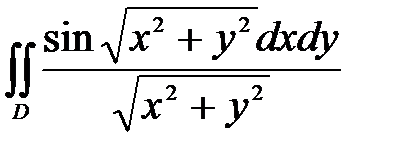 , , 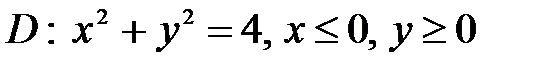
| |
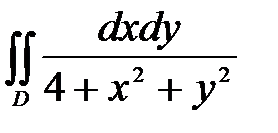 , , 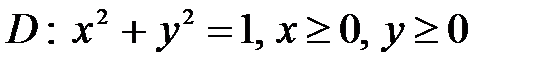
| |
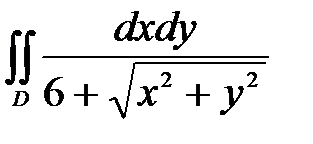 , , 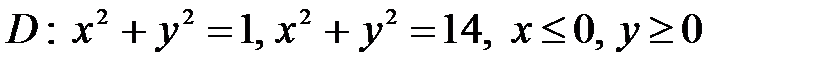
| |
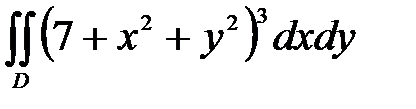 , , 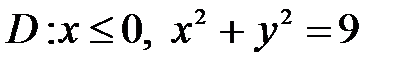
| |
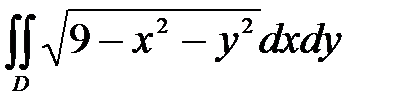 , , 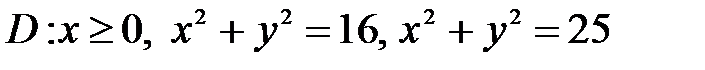
| |
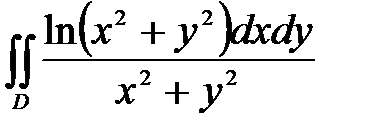 , , 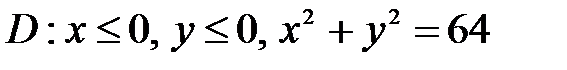
| |
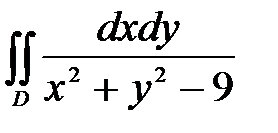 , , 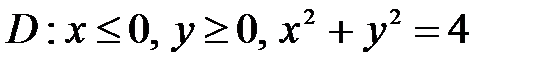
| |
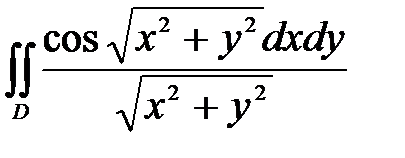 , , 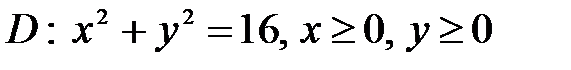
| |
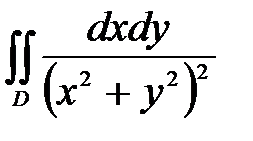 , , 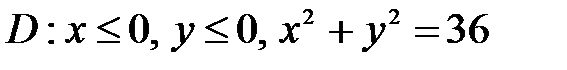
| |
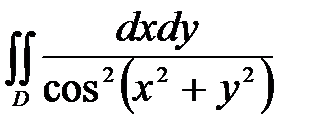 , , 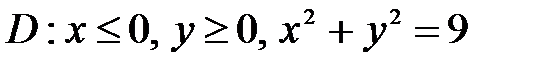
| |
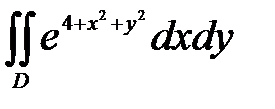 , , 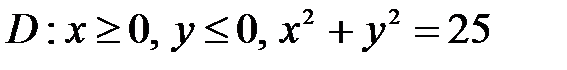
| |
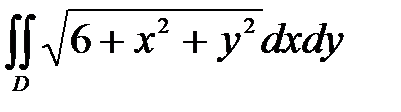 , , 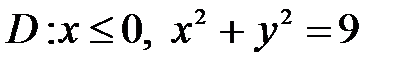
| |
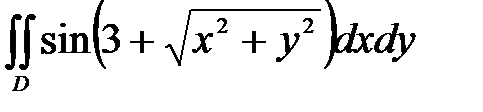 , , 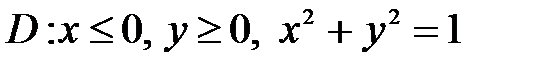
|
7. Вычислить тройные интегралы.
| № вар | Задания |
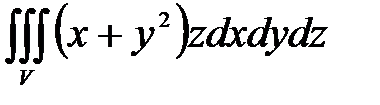 , , 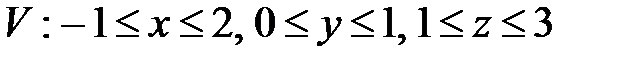
| |
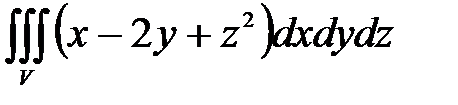 , , 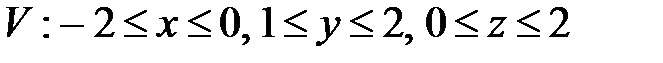
| |
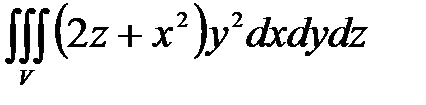 , , 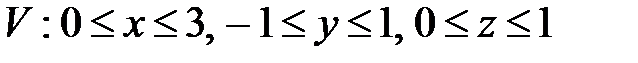
| |
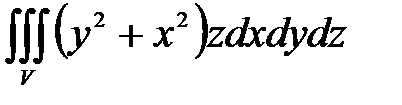 , , 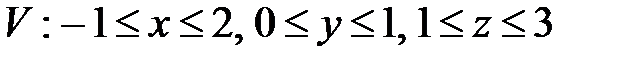
| |
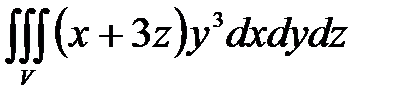 , , 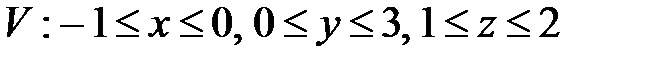
| |
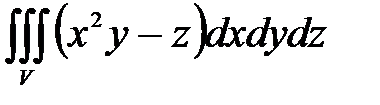 , , 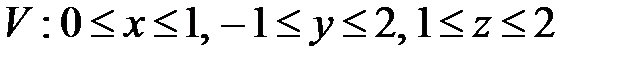
| |
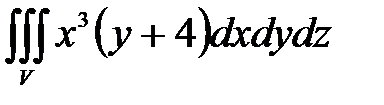 , , 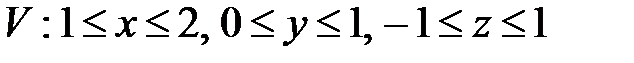
| |
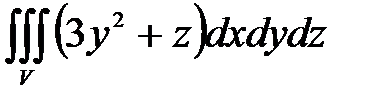 , , 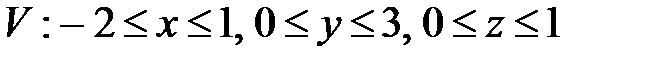
| |
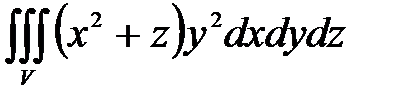 , , 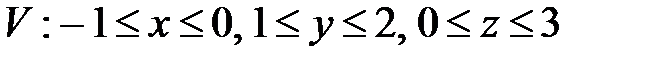
| |
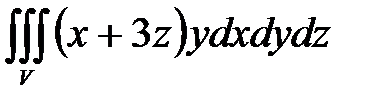 , , 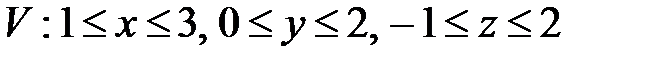
| |
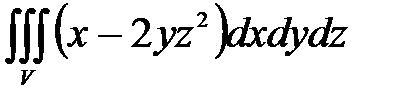 , , 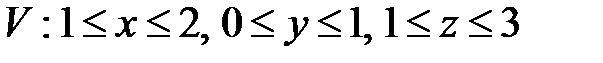
| |
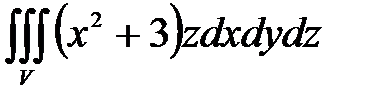 , , 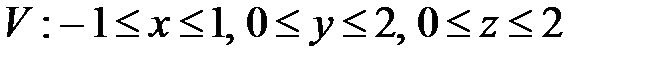
| |
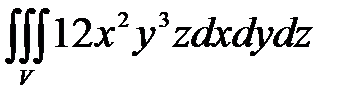 , , 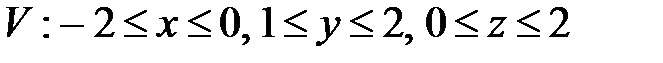
| |
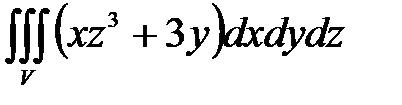 , , 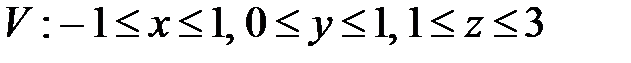
| |
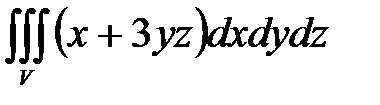 , , 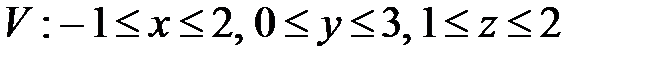
| |
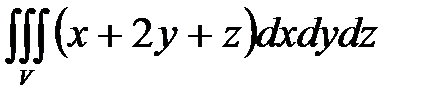 , , 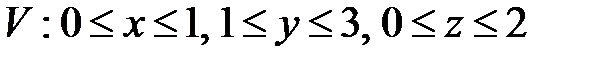
| |
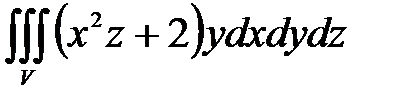 , , 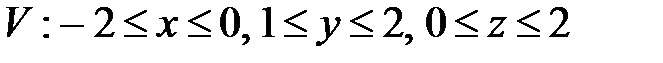
| |
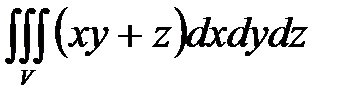 , , 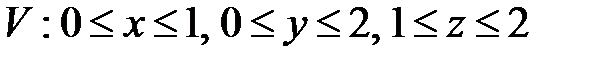
| |
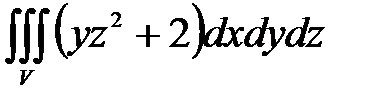 , , 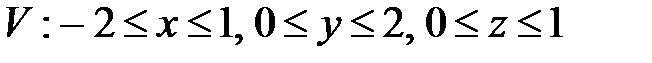
| |
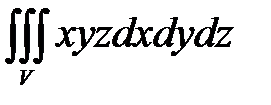 , , 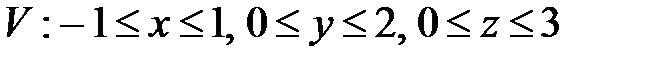
| |
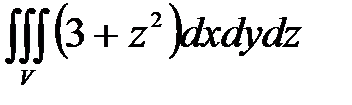 , , 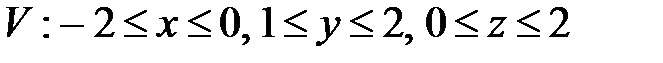
| |
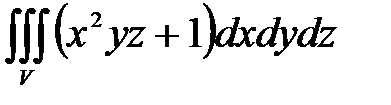 , , 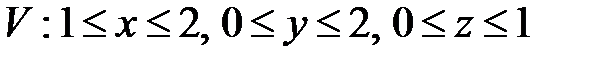
| |
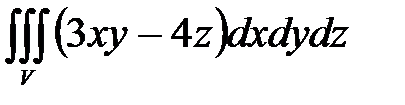 , , 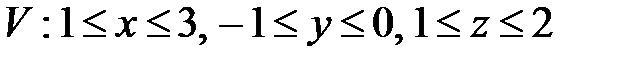
| |
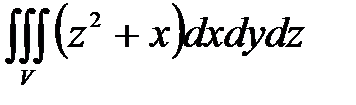 , , 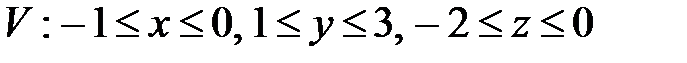
| |
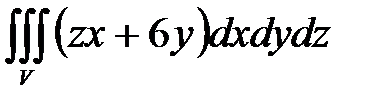 , , 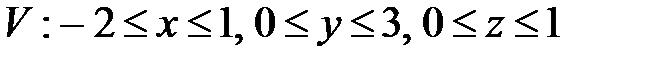
| |
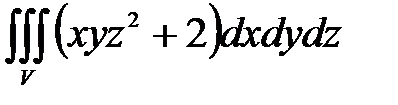 , , 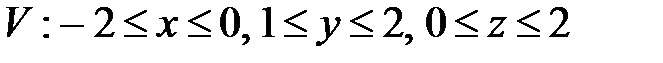
| |
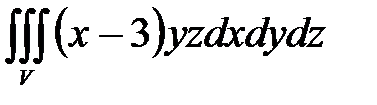 , , 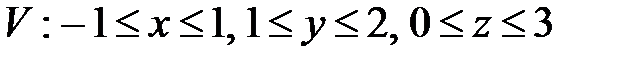
| |
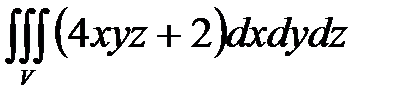 , , 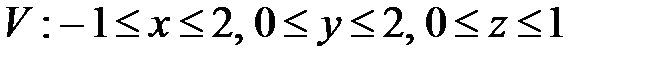
| |
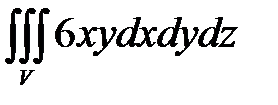 , , 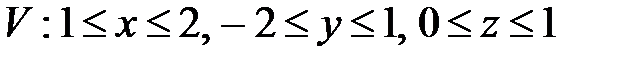
| |
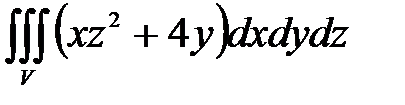 , , 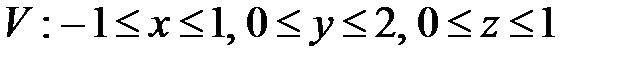
|
8. Вычислить криволинейные интегралы.
| № вар | Задания | |
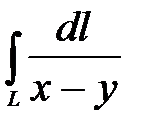 , если , если 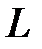 – отрезок прямой – отрезок прямой 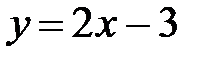 , заключенный между точками , заключенный между точками 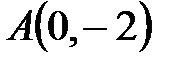 и и 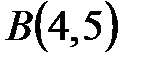 . .
| ||
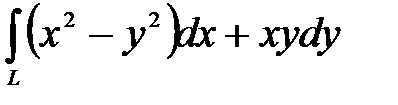 , где , где 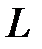 - отрезок прямой - отрезок прямой 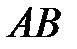 ; ; 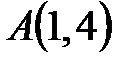 , , 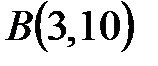 . .
| ||
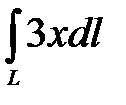 , если , если 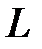 – отрезок дуга параболы – отрезок дуга параболы 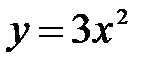 , заключенный между точками , заключенный между точками 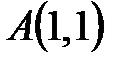 и и 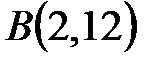 . .
| ||
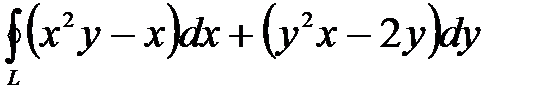 , где , где 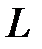 - дуга эллипса - дуга эллипса 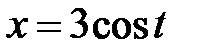 , , 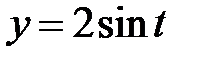 при положительном направлении обхода. при положительном направлении обхода.
| ||
 Сейчас читают про:
|
 2015-04-20
2015-04-20 407
407






