Динамика гармонических колебаний

Для определения характера движения механической системы нужно, исходя из законов динамики или закона сохранения энергии, составить уравнение движения системы, и если оно приводится к виду (7), то можно однозначно утверждать, что данная система является гармоническим осциллятором, часто­та ω которого равна корню квадратному из коэффициента при х. Рассмотрим несколько примеров с маятниками и затем обобщим получен­ные результаты.

Всякое твердое тело, колеблющееся под действием силы тяжести вокруг неподвижной точки или оси, называют маятником.

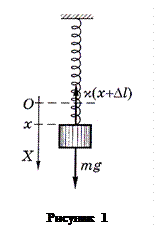
Грузик на пружине. Пусть грузик массы т, подвешенный на невесомой пружине жесткости k, совершает вер­тикальные колебания (рис. 2). Возьмем нача­ло О оси X в

положении равновесия, где 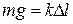, 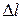– растяжение пружины в этом по­ложении. Тогда, согласно основному уравнению динамики, 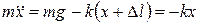, или

.

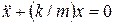Из сопоставления с (7) видим, что это урав­нение гармонического осциллятора, колеблю­щегося около положения равновесия с частотой ω и периодом Т,равными

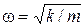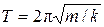, . (10)

Период колебаний Т не зависит от амплитуды а. Это свойство называется изохронностью колебаний. Изохронность, однако имеет место до тех пор, пока справедлив закон Гука. При больших растяжениях закон Гука нарушается. Тогда и колебания перестают быть изохронными, т. е. появляется зависимость периода колебаний от амплитуды.

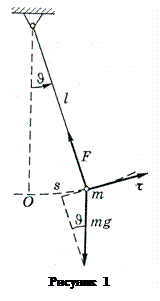Математический маятник. Материальная точка массы т, подвешенная на невесомой и нерастяжимой нити длиной l, совершает коле­бания в вертикальной плоскости (рис. 3). Здесь удобнее всего использовать уравнение динамики в проекции на орт τ, направление которого совпадает с положительным направлени­ем отсчета дуговой координаты s (величина алгебраическая, на рисунке изображен момент, когда s > 0). Начало отсчета s возь­мем в положении равновесия – в точке О. мея в виду, что 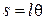, 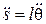и что про­екция силы натяжения 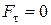, запишем: 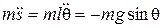,или

.

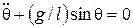Из сопоставления с (7) видим, что это уравнение, вообще говоря, не является уравнением гармонического осциллятора, поскольку в нем вместо смещения θ стоит 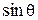. Однако при малых колебаниях, когда 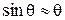, уравнение совпадает с (7):

,

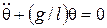откуда следует, что частота ω и период Т математического ма­ятника, совершающего малые колебания, равны

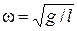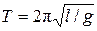, . (11)

Физический, маятник. Это твердое тело, совершающее коле­бания вокруг неподвижной оси, жестко свя­занной с телом. Рассмотрим колебания под действием силы тяжести (рис. 4). Выберем положительное направление отсчета угла θ против часовой стрелки (ось Z направлена к нам). Тогда проекция момента силы тяже­сти на ось Z запишется как 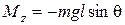и уравнение динамики вращательного дви­жения твердого тела примет вид

,

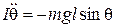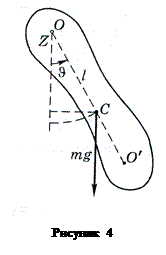где I — момент инерции тела относительно оси О, l — расстоя­ние между осью О и центром масс С. Ограничимся рассмотре­нием малых колебаний, при которых 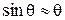. При этом усло­вии предыдущее уравнение можно записать так:

.

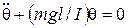Колебания будут гармоническими с частотой ω и периодом Т, равными

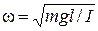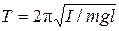, . (12)

Такую же частоту и период имеет математический маятник длины

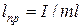, (13)

которую называют приведенной длиной физического маятника.

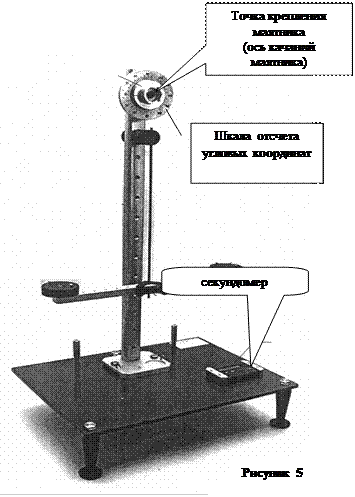
Точку О' (4), которая находится на прямой, проходя­щей через точку подвеса О и центр масс С, и отстоит от точки О на расстоянии 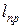,называют центром качания физического ма­ятника. Центр качания О' обладает замечательным свойством: если маятник перевернуть и заставить совершать малые коле­бания вокруг оси О', то период колебаний не изменится. На этом свойстве основано определение ускорения свободного па­дения с помощью оборотного маятника: экспериментально устанавливают положения двух «сопряженных» точек (осей) О и О', малые колебания вокруг которых происходят с одинако­вой частотой. Это значит, что расстояние ОО' = 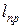. Определив ω и 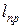, из формулы 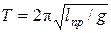(14)

находим g.

Рассмотренные примеры относятся к сво­бодным колебаниям без трения, которые происходят в системе, предоставленной самой себе после того, как она была тем или иным способом выведена из состояния равновесия. Можно утверждать, что свободные колебания любого осциллятора в от­сутствие трения будут гармоническими, если действующая в нем сила (или момент силы) является квазиупругой, т. е. си­лой, направленной к положению равновесия и зависящей от смещения из этого положения линейно.

Именно квазиупругий характер силы (или момента силы) служит и критерием малых колебаний.

Кроме того, частота и период свободных колебаний без тре­ния зависят только от свойств самого осциллятора в отличие от амплитуды колебаний и начальной фазы, которые определяют­ся начальными условиями.

В данной работе колебания физического и математического маятников можно считать свободными, если угол их отклонения от положения равновесия будет менее 10º.