Определение ускорения свободного падения для Астрахани при помощи математического и физического маятников
Цель работы: изучение свободных колебаний на примере малых колебаний математического и физического маятников, определение ускорения свободного падения.
Оборудование: платформа на регулирующихся ножках, закрепленная на ней стойка со шкивом и угломерной шкалой на конце; закрепленные на платформе часы-таймер; математический маятник (планка (m = 30.7 г) с диском (m = 484.9 г) на конце), физический маятник (тяжелый стержень с отверстиями (m = 234.6 г, l = 340 мм)), пластмассовая втулка для фиксации маятников на оси.
Колебания
Колебание – более или менее регулярно повторяющийся процесс. Таково качественное определение понятия «колебание». Можно привести множество примеров колебательных процессов, относящихся к различным областям жизнедеятельности. Колеблется маятник часов; колеблется груз, подвешенный на пружине; колеблется взволнованная поверхность воды и гитарная струна; колеблется заряд на пластинах конденсатора и магнитное поле в катушке индуктивности колебательного контура; более или менее периодически изменяется температура воздуха (зимой холоднее - летом теплее) и количество автомобилей на улицах города (больше в часы пик — меньше поздней ночью); периодически меняется экономическая ситуация в жизни общества: кризисные явления сменяются подъемом экономики. Колеблется давление (или плотность воздуха), вызывая колебания ушной мембраны – и мы слышим голоса окружающих.
Простейший вид колебательных движений – гармонические колебания.
Кинематика гармонических колебаний
Гармоническими называют колебания, в которых интересующая нас величина х (например, линейное или угловое смещение из положения равновесия) изменяется со временем t по закону
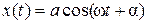 , (1)
, (1)
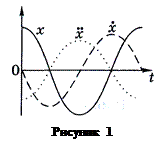 где a, ω, φ— константы. График функции (1) изображен на рис. 1. Она хороша, разумеется, не только потому, что имеет довольно простой математический вид. Более существенно то обстоятельство, что реальные колебания во многих физических системах зачастую очень хорошо описываются этой функцией, т. е. близки к гармоническим колебаниям. Легко проверить, что функция (1) является периодической, т. е. для любого момента времени t имеет место равенство x (t) = x (t+T), где Т называется периодом колебаний:
где a, ω, φ— константы. График функции (1) изображен на рис. 1. Она хороша, разумеется, не только потому, что имеет довольно простой математический вид. Более существенно то обстоятельство, что реальные колебания во многих физических системах зачастую очень хорошо описываются этой функцией, т. е. близки к гармоническим колебаниям. Легко проверить, что функция (1) является периодической, т. е. для любого момента времени t имеет место равенство x (t) = x (t+T), где Т называется периодом колебаний:
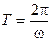 . (2)
. (2)
Величина ω, с-1называется циклической (круговой) частотой. Положительная константа а – амплитуда колебания (это максимальное отклонение величины x от равновесного значения x = 0). Аргумент косинуса в (1)– угол φ, выраженный в радианах, называется фазой колебания:
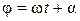 , (3)
, (3)
а значение φ при t = 0, т. е. величину α, называют начальной фазой. Соотношение (3) — это линейная связь между фазой колебания φ и круговой частотой ω, из которой следует 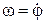 . Круговая частота – это производная фазы φ по времени. Число колебаний в секунду
. Круговая частота – это производная фазы φ по времени. Число колебаний в секунду 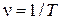 называют линейной частотой (иногда просто частотой). Единица линейной частоты – Гц (герц). Очевидно,
называют линейной частотой (иногда просто частотой). Единица линейной частоты – Гц (герц). Очевидно,
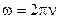 (4)
(4)
(колебанию 1 герц соответствует изменение фазы – угла поворота, равное 2πвсекунду). Обратите внимание на различие наименований циклической и линейной частот.
Продифференцировав (1) по времени, найдем скорость 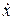 и ускорение
и ускорение 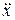 :
:
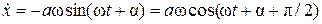 , (5)
, (5)
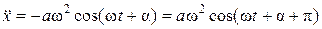 , (6)
, (6)
Из этих выражений видно, что скорость 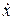 и ускорение
и ускорение 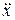 также изменяются по гармоническому закону с амплитудами
также изменяются по гармоническому закону с амплитудами 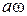 и
и 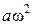 соответственно. При этом скорость опережает смещение х по фазе на
соответственно. При этом скорость опережает смещение х по фазе на 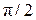 , а ускорение – на
, а ускорение – на 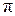 , т. е. находится в про-тивофазе со смещением х. На рис. 1 приведены графики зависимостей
, т. е. находится в про-тивофазе со смещением х. На рис. 1 приведены графики зависимостей 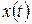 ,
, 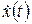 и
и 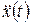 для случая α = 0.
для случая α = 0.
Сопоставив (6) и (1), видим, что 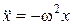 , или
, или
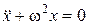 . (7)
. (7)
Это дифференциальное уравнение называют уравнением гармонического осциллятора. Его решение (1) содержит две произвольные постоянные: а и α. Для каждого конкретного колебания они определяются начальными условиями — смещением х 0и скоростью 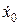 в начальный момент t = 0:
в начальный момент t = 0:
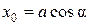 ,
, 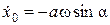 . (8)
. (8)
Отсюда находим искомые постоянные:
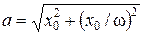 ,
, 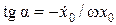 . (9)
. (9)
Обычно рассматривают только значения α в интервале 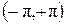 . Уравнение для
. Уравнение для 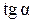 удовлетворяется двумя значениями α в этом интервале. Из этих значений следует взять то, при котором получаются правильные знаки у
удовлетворяется двумя значениями α в этом интервале. Из этих значений следует взять то, при котором получаются правильные знаки у 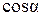 и
и 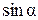 в (8).
в (8).
 2015-04-20
2015-04-20 3130
3130