2015-04-30
544
Лекция 1.
Тема. Обыкновенные дифференциальные уравнения. Основные понятия.
Напомним различные формы записи производных: первого порядка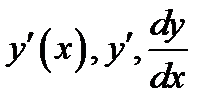 
; второго порядка 
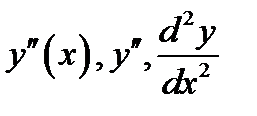и т.д.
Определение 1.1. Уравнение, в котором неизвестная искомая функция входит под знаком производной или дифференциала, называется дифференциальным уравнением.
Определение 2. Если эта неизвестная искомая функция зависит от одной переменной, то уравнение называется обыкновенным дифференциальным уравнением (ОДУ).
Пример 1.
1) 
;
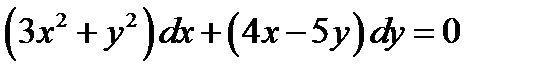2) 
;
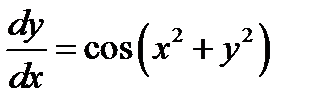3) 
;
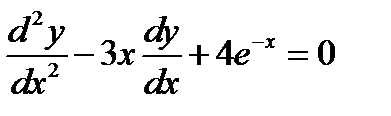5) 
.
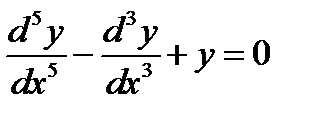Пример 2. Уравнение 
не является дифференциальным уравнением. Почему?
Определение 1.3. Порядком (ОДУ) назовем порядок старшей производной искомой функции
входящей в ОДУ.
Пример 3. ОДУ 1) и 2), рассмотренные в примере 1 являются ОДУ первого порядка. ОДУ 3)
второго порядка. ОДУ 4) пятого порядка.
Определение 1.4. Совокупность двух или более дифференциальных уравнений называется
системой обыкновенных дифференциальных уравнений.
Пример 4.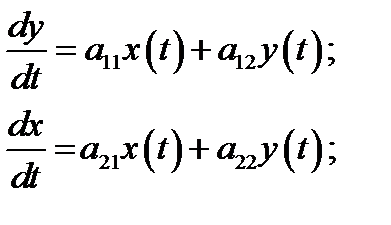 
Данное занятие посвящено ОДУ первого порядка.
|
|
|
Рассмотрим ОДУ
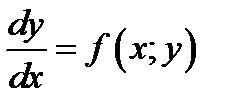(1.1)
первого порядка. Его также можно записать в дифференциальном виде
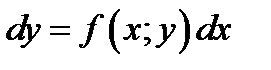
Или более общё
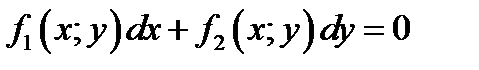(1.2)
Определение 1.5. Областью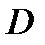 
-действия ОДУ (1.1) назовём область в которой определена функция 
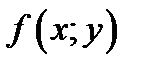,стоящая в правой части ОДУ.
Пример 5. Найдем область 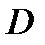для ОДУ 
.
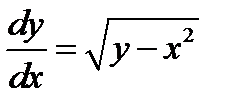Решение. Областью задания функции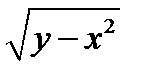 
является множество точек 
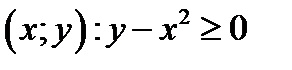. Именно в этой области и определено действие нашего ОДУ.
Определение 1.6. Функцию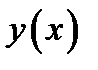 
, определённую на интервале 
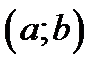, назовём решением ОДУ, если выполняются следующие условия:
1) точка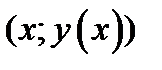 
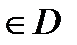для любых 
;
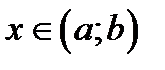2) функция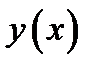 
дифференцируема на интервале ;
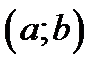3) для любых 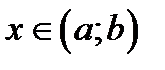имеет место истинное равенство
.
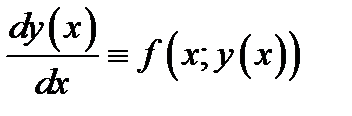Пример 6. Доказать что функция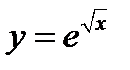 
, определённая на интервале 
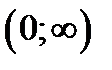, является решением ОДУ 
.
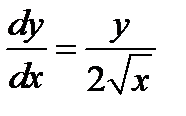Доказательство. Область определения правой части ОДУ есть интервал 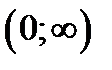. Следовательно
1-ый пункт определения 6 выполнен: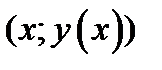 
; 
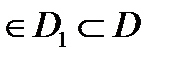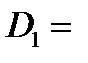
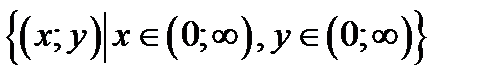. Функция 
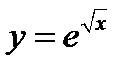дифференцируема. Далее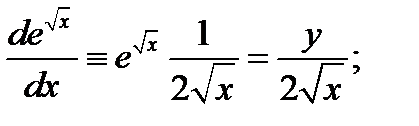 
Определение 1.7. График решения ОДУ назовём интегральной кривой. Таким образом интегральная кривая это геометрическое место точек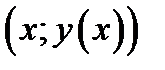 
, где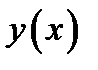 
- решение ОДУ.
