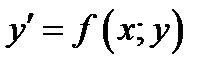Уравнение

(1.1)

Определяет в каждой точке 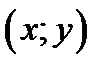координатной области 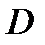значение производной 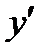, то есть угловой коэффициент касательной к интегральной кривой, проходящей через эту точку.

Пример 1. Наклон касательной к интегральной кривой уравнения 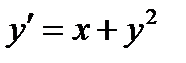в точке 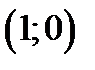легко вычислить используя уравнение .

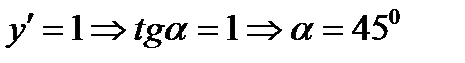Определение 1.8. Если в каждой точке области D задано значение некоторой величины, то говорят, что в области D задано поле этой величины. Таким образом ОДУ (1.1) задаёт поле направлений касательных к интегральным кривым.

Пример 7. Пусть 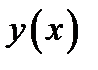есть решение ОДУ. Тогда в любой точке интегральной кривой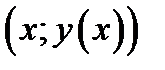

тангенс угла наклона касательной (см.(1.1)) равен 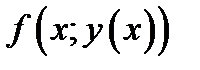. Возьмём произвольно точку 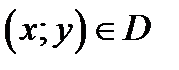и поместим в ней начало вектора 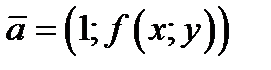. Тогда вся область 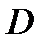будет заполнена этими векторами .

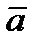Определение 1.9. Множество векторов 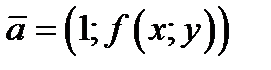расположенных в области 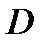называют

полем направлений обыкновенного дифференциального уравнения.

Задача интегрирования ОДУ(1.1) может быть теперь истолкована так: найти такую интегральную кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.

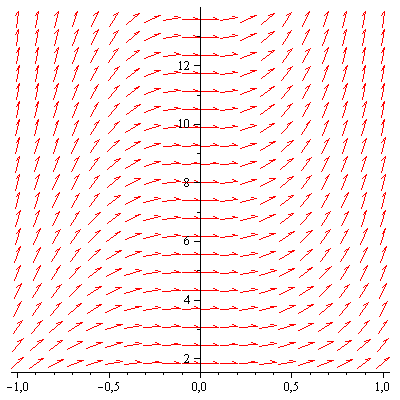Пример 8. На рис1. приведен чертёж поля направлений ОДУ

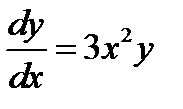
Рис. 1

Используя поле направлений можно приближённо получить интегральные кривые любого

ОДУ. Если среди множества интегральных кривых нужно выделить конкретную интегральную кривую, то для этого нужно заранее задать точку 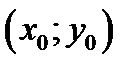на этой прямой. Задача выделения конкретной интегральной кривой называется задачей Коши. Строгое определение этой задачи дадим позже (см. определение 9).

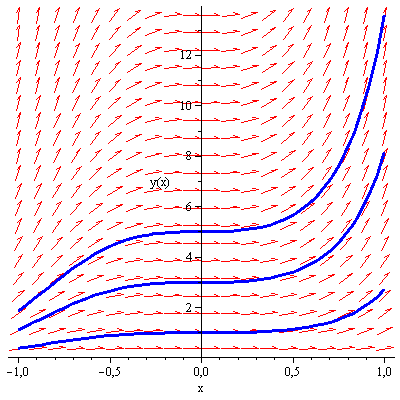На рис.2 представлены интегральные кривые предложенных начальных задач (смотреть снизу вверх), построенных с использованием поля направлений:

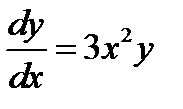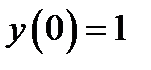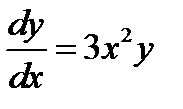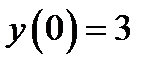1) , ; 2) , ; 3) ,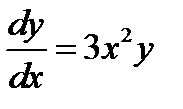

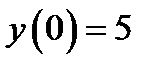
Рис.2

Как видно из рисунка интегральные кривые не пересекаются. Если мы хотим выделить из всего этого множества конкретную интегральную кривую, то мы должны фиксировать конкретную точку на ОХУ и выбрать единственную интегральную кривую, проходящую через эту точку.

Пример 8. Дифференциальное уравнение 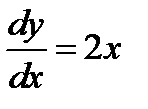задаёт нам множество решений 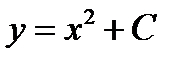. Здесь 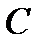- произвольная постоянная. Эти интегральные кривые заполняют область 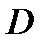сплошным образом. Если нам понадобится конкретная интегральная кривая, то нужно заранее задать точку, через которую эта кривая проходит. Например, если за начальную точку взять точку 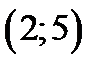, то конкретная интегральная кривая будет задаваться уравнением 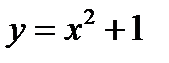. Если взять точку 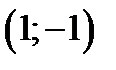, то уравнение становится таким .

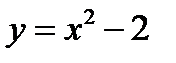Следующее определение является фундаментальным.

Определение 9. Назовём задачу нахождения решения ОДУ (1.1) задачей Коши или (начальной задачей), если выполняются два условия

1) ;

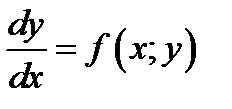2) .

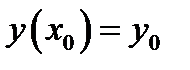Определение 1.10. Назовём частным решением ОДУлюбое решение задачи Коши.

Определение 1.11. Назовём общим решением ОДУ дифференцируемую функцию 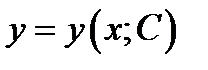,зависящую отпроизвольной постоянной и удовлетворяющей условиям

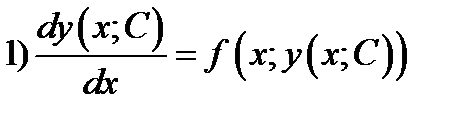, для любого ;

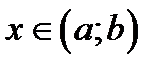2)решение любой задачи Коши можно получить из формулы

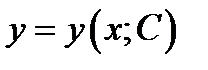подбором постоянной .

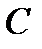Пример 9. Доказать, что функция 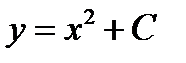является общим решениемдифференциального уравнения .

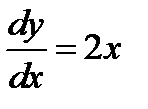Условие 1) выполнено 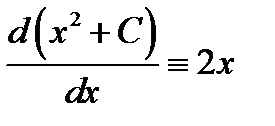. 2) Пусть для произвольной точки 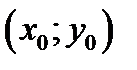выполняется условие 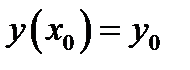. Нужно доказать, что можно подобрать постоянную 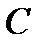в решении 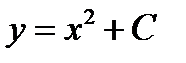, чтобы выполнялось условие 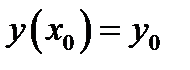. Подставляя вместо 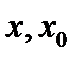, а вместо 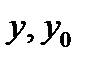получаем 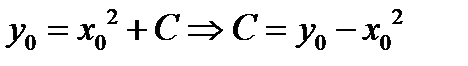. Таким образом из формулы 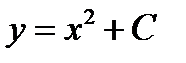, являющейся решением ОДУ 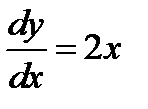получается любое частное решение.

Часто в результате интегрирования ОДУ решение получается в виде неявно заданной функции.

В этом случае решение будем также называть общим решением, и записывать соотношением

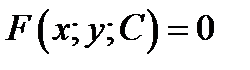
Теорема 1. Если:

1) функция 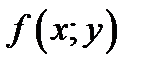непрерывна в области ;

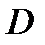2) частная производная 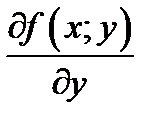непрерывна в области ,

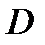тогда любая задача Коши

1) ;

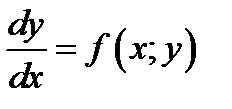2) .

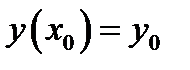имеет только одно решение.

При выполнении условий теоремы 1 справедливо утверждение.

Если две интегральные кривые совпадают в одной точке, то они совпадают тождественно.

Если условия теоремы 1 нарушаются, то в области 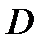могут возникать особые решения.

Определение 1.12. Пусть 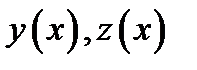два различных решенияОДУ. Решение 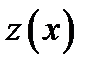называется особым решением, если существуют общие точки интегральной кривой 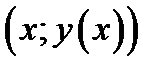и интегральной кривой 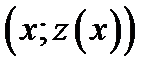и кривые не совпадают тождественно.

ОДУ первого порядкараспадаются на типы. Каждый тип имеет свои правила решения. Мы рассмотрим два типа наиболее встречающихся ОДУ.

1) ДУ с разделяющимися переменными. Их всегда можно записать в виде

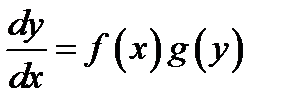(1.3)

2) Линейные ОДУ. Их всегда можно записать в виде

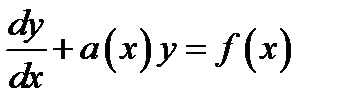(1.4)

Поскольку основным приёмом при решении ДУ является интегрирование, то решение ОДУ часто называют интегралом.

Алгоритм решения ОДУ с разделяющимися переменными (1.3).

1шаг. В уравнении (1.3) разделяем переменные

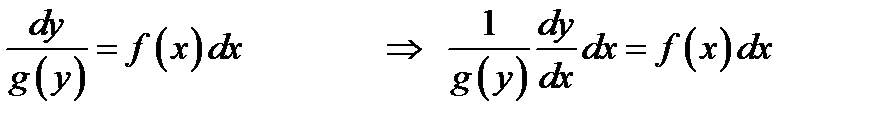
2шаг. Интегрируем обе части равенства по переменной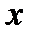

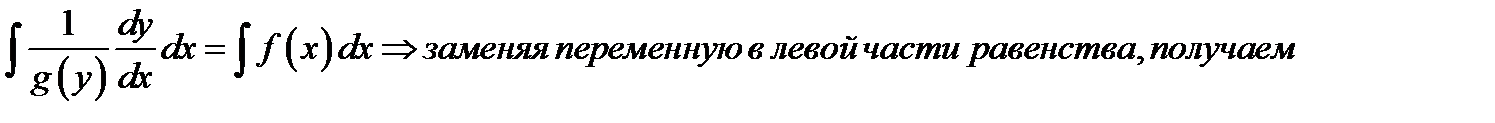
общий интеграл (общее решение) данного ОДУ

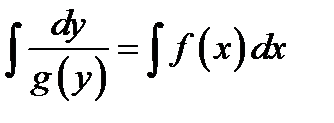
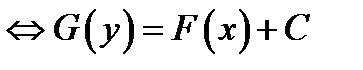(1.5)

Перейдем к практическому решению ДУ с разделяющимися переменными.

Пример 10. Найти общее решение ДУ .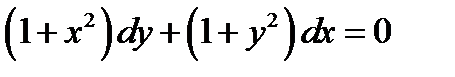

Решение. Порядок данного ОДУ- первый. Тип -ОДУ с разделяющимися переменными.

Применяем соответствующий алгоритм решения.

1 шаг. Разделяем переменные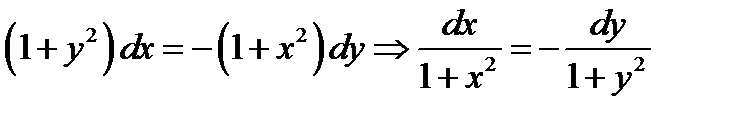

2 шаг. Интегрируем обе части

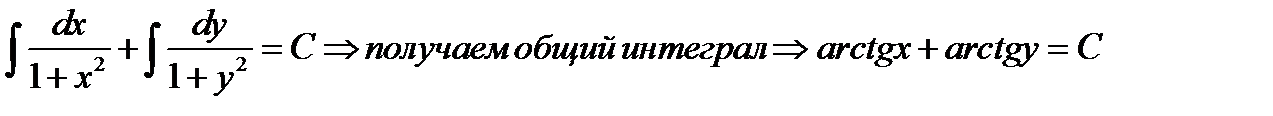
Пример 11. Решить начальную задачу ,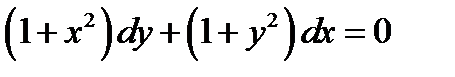

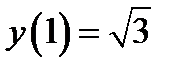
Решение. Порядок данного ОДУ- первый. Тип - ОДУ с разделяющимися переменными.

Выписываем общий интеграл данного ДУ.

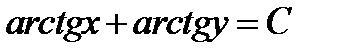
Так как решения всех начальных задач содержатся в общем интеграле, то подставляя

в полученное общее решение 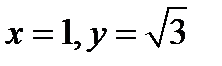определяем постоянную С, которая фиксирует нужное значение.

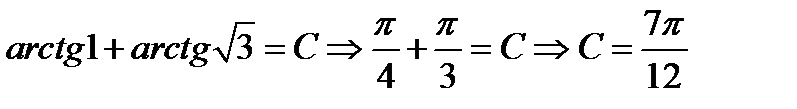
Отсюда получаем единственное частное решение поставленной начальной задачи

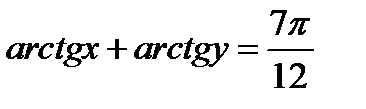
Перейдем к изучению алгоритма нахождения общего решения линейного ОДУ (1.4).

1шаг. Вычисляем интегрирующий множитель 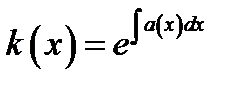. Используя цепное правило

Получаем

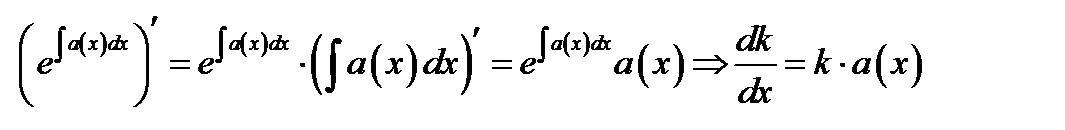. (1.6)

2шаг. Умножаем обе части ОДУ на интегрирующий множитель

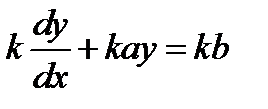
Отсюда, учитывая (1.6) имеем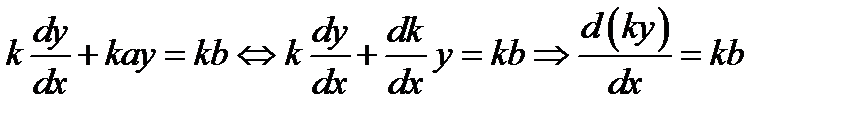

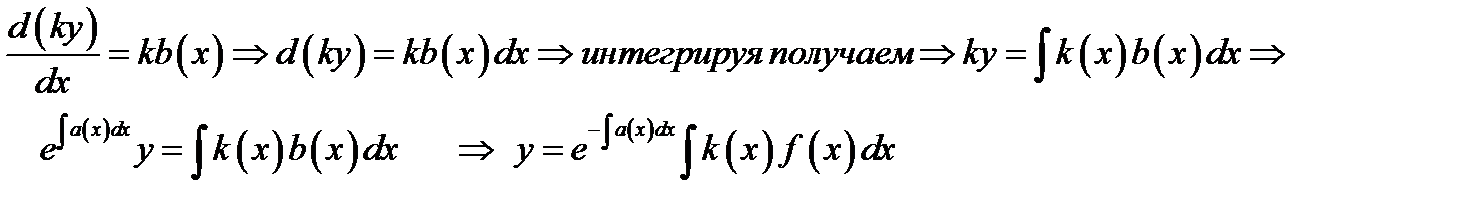
Общее решение линейного ОДУ всегда имеет явное выражение

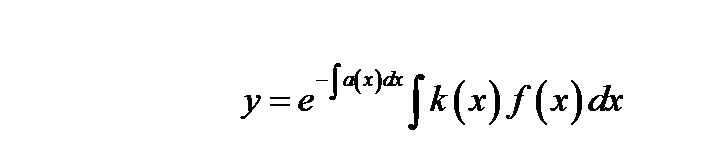(1.7)

Пример 12. Найти общий интеграл ОДУ .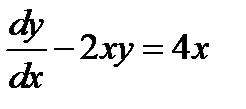

Решение.Порядок данного ОДУ- первый. Тип данного ОДУ - линейное ОДУ.

1 шаг. Вычисляем интегрирующий множитель 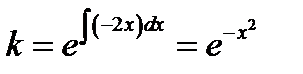и умножаем на него обе части уравнения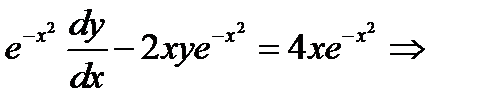

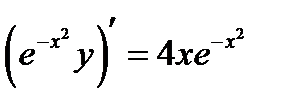
2 шаг. Интегрируем обе части полученного уравнения по x

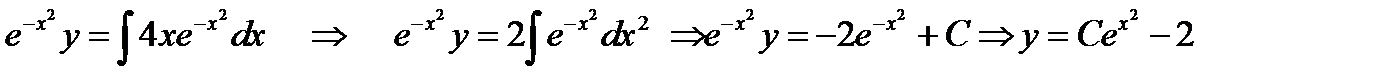
Ответ: общее решение имеет вид .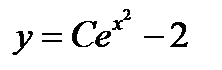

Пример 13. Решить начальную задачу , .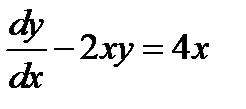

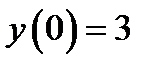Решение. Порядок данного ДУ- первый. Тип данного ОДУ - линейное ОДУ

Находим общее решение (см. пример 12) 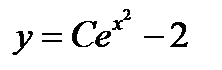. Подставляем в него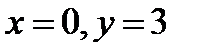

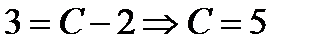. Откуда частное решение начальной задачи имеет вид .

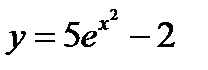Проверка.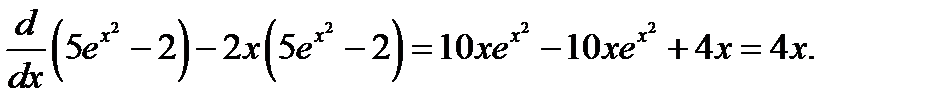

Проверяем справедливость начальных условий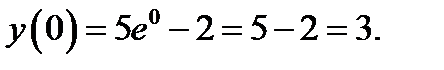

Контрольные вопросы.

I. Дайте определение ОДУ первого порядка. Как определяется начальная задача Коши для ОДУ первого порядка. Что называется частным решением, общим решением, особым решением ОДУ?.

II. Что называется общим интегралом ОДУ, интегральной кривой? Что такое поле направлений, задаваемое ОДУ.

III. Какие ОДУ называются уравнениями с разделяющимися переменными? Укажите метод их решения.

IV. Как определяются линейные ОДУ первого порядка? Укажите метод их решения.