1 шаг. Интегрируем первое из уравнений (7.10) по переменной 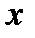 , считая
, считая 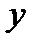 постоянной
постоянной
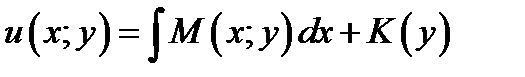 (7.11)
(7.11)
Здесь 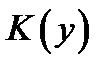 постоянная интегрирования, зависящая в данной ситуации от фиксированной
постоянная интегрирования, зависящая в данной ситуации от фиксированной 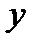 .
.
2 шаг. Дифференцируя полученное выражение по 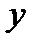 , получим
, получим
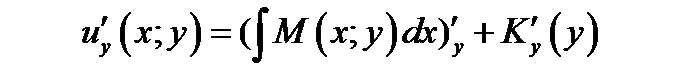 (7.12)
(7.12)
3 шаг. Подставляя полученное равенство (7.12) во второе равенство (7.10) мы находим 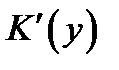 . Интегрируя затем
. Интегрируя затем 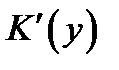 по
по 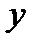 определяем
определяем 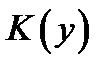 и, следовательно искомую функцию
и, следовательно искомую функцию 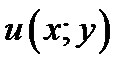 . Используя
. Используя
Формулу (7.7) записываем общее решение ОДУ в полных дифференциалах (7.8).
Пример 4. Найти общее решение ОДУ в полных дифференциалах 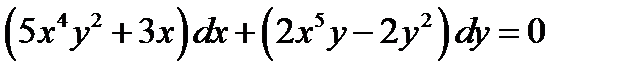 .
.
Решение. Убедимся, что данное уравнение есть уравнение в полных дифференциалах. Для
этого проверим выполнение условия (7.10)
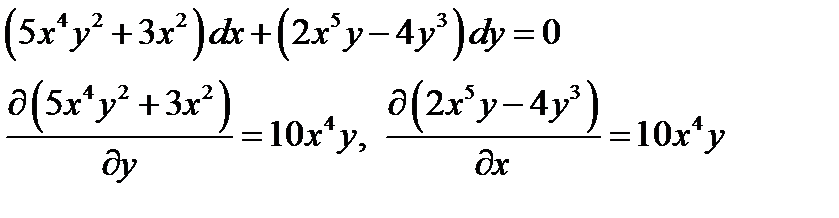
Условие (7.10) выполняется. Используем правило
1шаг. 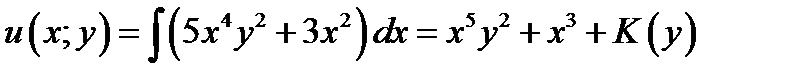 .
.
2 шаг. Дифференцируем полученное выражение по 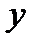
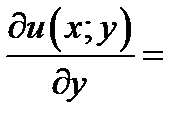
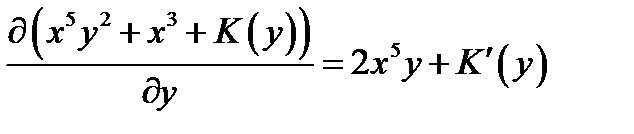
3 шаг. 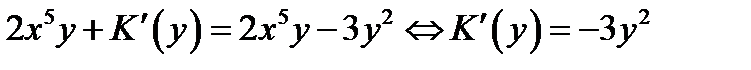 . Интегрируя последнее равенство
. Интегрируя последнее равенство
определяем первообразную 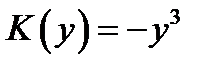 .
.
Отсюда определяем 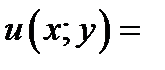
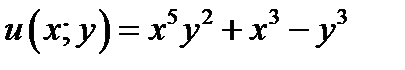 . Согласно формуле (7.7)
. Согласно формуле (7.7)
общий интеграл имеет вид
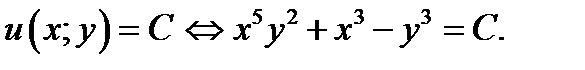
 2015-04-30
2015-04-30 424
424








