Уравнения второго порядка, порядок которых может быть понижен

Приведем типы ОДУ, допускающих понижение порядка.

I. ОДУ типа

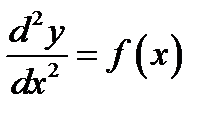
Решаются последовательным интегрированием.

Пример 1. Найти общее решение ОДУ ;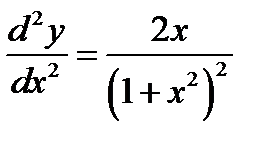

Решение. Интегрируем обе части по переменной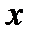

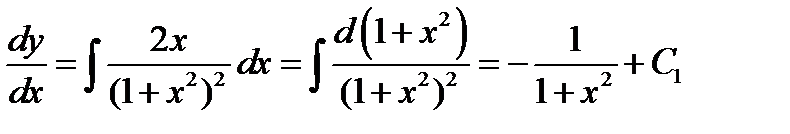
Интегрируя полученное равенство повторно, находим общий интеграл

.

II. Если ОДУ не содержит явно функцию (то есть имеет вид 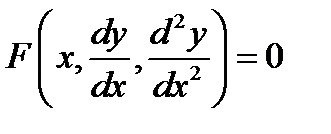), то

оно сводится к уравнению первого порядка заменами .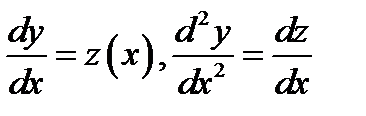

Пример 2. Найти общее решение ОДУ .

Решение. Полагаем в ОДУ: 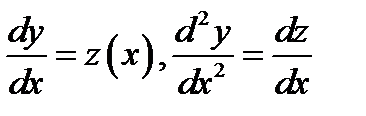; Исследуемое уравнение становится линейным

уравнением 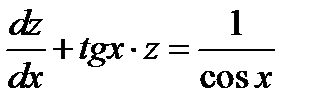. Его общим решением является функция

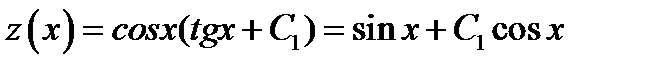. Отсюда, возвращаясь к старой функции, получаем

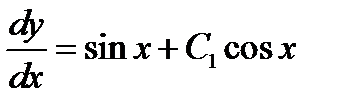. Формула общего решения имеет вид .

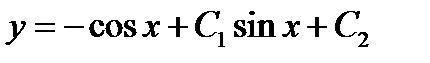III. ОДУ , в формулу которых не входит 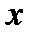, сводится к уравнению первого порядка заменами ;

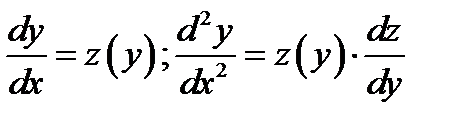Пример 3. Найти общее решение ОДУ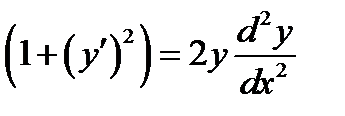

Решение. Полагаем в ОДУ 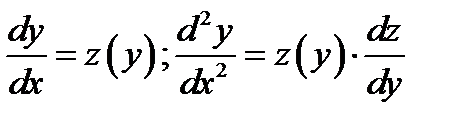. Исследуемое уравнение становится

ОДУ с разделяющимися переменными 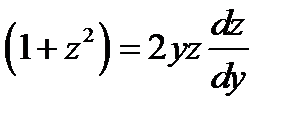. Разделяя переменные и интегрируя, получаем 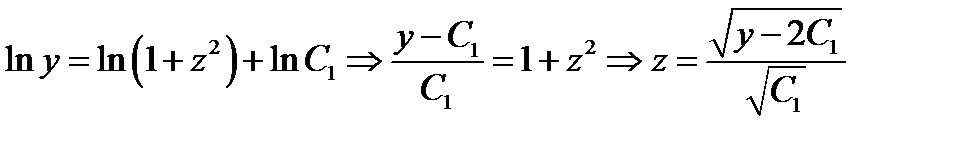. Отсюда, возвращаясь к старой функции, будем иметь

.

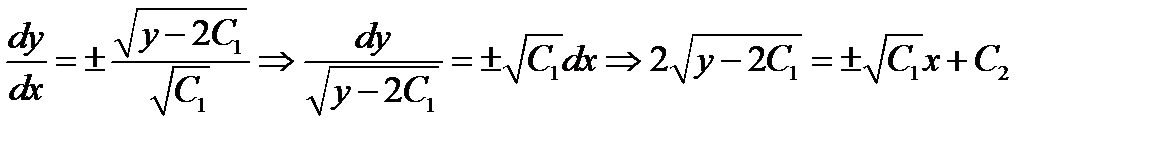Возводя в квадрат, получаем ответ .