Правило вывода (правило принятия решения). Полученную величину отношения (расчетное значение) сравнивают с критическим (табличным) значением отношения (см

Полученную величину отношения (расчетное значение) сравнивают с критическим (табличным) значением отношения (см. таблицу критических значений — Приложение 1).

Правило вывода: Если вычисленное отношение больше, чем табличное значение отношения, то проверяемое значение признается выскакивающим и его можно исключить из последующей обработки данных.

Если расчетное значение отношения меньше или равно табличному значению отношения, то проверяемое значение отбрасывать нельзя.

Решение лучше принимать на 1%-ном уровне значимости — высокий уровень достоверности вывода.

На уровне значимости 5 % возможна грубая ошибка.

Пример. Сравним два ряда значений.

Даны значения 1 3 3 5 6 7 8 Среднее арифметическое = 4,74 Мода = 3 Медиана = 5

Даны значения 1 3 3 5 6 7 18 Среднее арифметическое = 6,14 Мода = 3 Медиана = 5 Оценим «на выскакивание» самое большое значение, далеко отстоящее от ближайшего к нему значения. Для этого найдем отношение расстояний по формуле Iа: 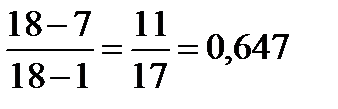Табличное значение отношения 0,507 на уровне 5% и 0,637 на уровне значимости 1%. Расчетное значение больше табличного (при 1%-м уровне). Следовательно, значение 18 следует исключить из дальнейшей обработки данных, так как оно является выскакивающим.

Как видно из приведенного примера, такие параметры как медиана и мода в обоих рядах значений одинаковы, а вот среднее арифметическое значение «чувствительно» к каждому значению в выборке и выскакивающие значения будут искажать основные тенденции выраженности признака в исследуемой группе.

Процедуру проверки крайних значений на выскакивание рекомендуется применять, если: а) имеются далеко отстоящие крайние значения; б) объем выборки небольшой.