Последовательность анализа марковской СМО не зависит от конкретного типа СМО и состоит из следующих этапов:
1. Конструируется пространство состояний СМО;
2. Определяются вероятности переходов из состояния в состояние за некоторое достаточно малое время D t;
3. Составляются уравнения полных вероятностей пребывания системы в состояниях i в момент t + D t;
4. Выводятся дифференциальные уравнения для вероятностей пребывания системы в состоянии i;
5. Система дифференциальных уравнений решается для установившегося режима, при котором производные вероятностей обращаются в нуль;
6. Рассчитанные значения установившихся вероятностей определяют искомые показатели качества системы.
Рассмотрим многоканальную СМО с конечной очередью (рис. 9). Система имеет 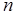 каналов и
каналов и 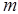 мест в очереди. Интенсивность входящего потока заявок -
мест в очереди. Интенсивность входящего потока заявок - 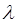 , интенсивность обслуживания -
, интенсивность обслуживания - 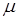 . Дисциплина обслуживания - заявки поступают на обслуживание в порядке их поступления в систему. Если заявка приходит в момент, когда заняты все
. Дисциплина обслуживания - заявки поступают на обслуживание в порядке их поступления в систему. Если заявка приходит в момент, когда заняты все 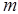 мест в очереди, то она получает отказ и покидает систему.
мест в очереди, то она получает отказ и покидает систему.
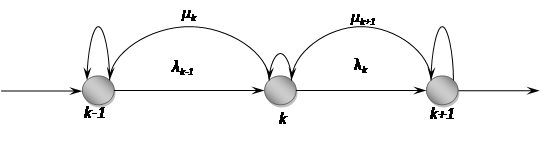
Рис. 9 Граф состояний многоканальной СМО с ожиданием.
Поток входящих заявок - пуассоновский, закон распределения длительности обслуживания - показательный. Система может находится в следующих состояниях:
«нет очереди»:
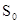 —все каналы свободны;
—все каналы свободны;
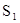 — занят один канал, остальные свободны;
— занят один канал, остальные свободны;
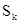 — заняты
— заняты 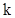 каналов, остальные нет;
каналов, остальные нет;
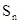 — заняты все
— заняты все 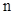 каналов, свободных нет;
каналов, свободных нет;
«есть очередь»:
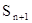 —заняты все n каналов; одна заявка стоит в очереди;
—заняты все n каналов; одна заявка стоит в очереди;
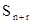 — заняты все n каналов, r заявок в очереди;
— заняты все n каналов, r заявок в очереди;
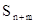 —заняты все n каналов, r заявок в очереди.
—заняты все n каналов, r заявок в очереди.
Определим установившиеся вероятности состояний процесса функционирования марковской СМО. Обозначим через 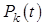 - вероятность того, что в момент t система находится в
- вероятность того, что в момент t система находится в 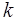 - состоянии. Придадим t малое приращение D t и найдем вероятность того события, что в момент t + D t система будет находится в
- состоянии. Придадим t малое приращение D t и найдем вероятность того события, что в момент t + D t система будет находится в 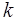 - состоянии. Это событие, при достаточно малых D t может реализоваться следующими тремя вариантами:
- состоянии. Это событие, при достаточно малых D t может реализоваться следующими тремя вариантами:
1) в момент t система была в (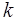 -1) состоянии и за время D t перешла из него в
-1) состоянии и за время D t перешла из него в 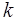 - состояние:
- состояние:
(6) 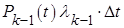
где:
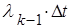 приближенно равна условной вероятности перехода из (
приближенно равна условной вероятности перехода из (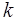 -1) в
-1) в 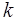 - состояние за времяD t;
- состояние за времяD t;
2) в момент t система была в (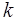 +1) состоянии и за время D t перешла из него в
+1) состоянии и за время D t перешла из него в 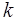 - состояние, аналогично:
- состояние, аналогично:
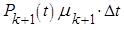 (7)
(7)
3) в момент t система была в 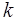 - состоянии и за время D t не перешла из него ни в (
- состоянии и за время D t не перешла из него ни в (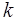 +1)-ое ни в (
+1)-ое ни в (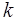 -1)-ое состояния.
-1)-ое состояния.
Вероятность того, что за время D t не осуществится ни один из этих переходов, равна 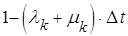 и, поэтому вероятность этого варианта:
и, поэтому вероятность этого варианта:
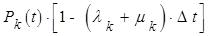 (8)
(8)
Применяя правило сложения вероятностей получим:
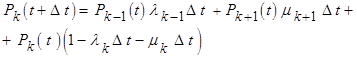 (9)
(9)
После раскрытия скобок и переноса 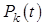 в левую часть получим:
в левую часть получим:
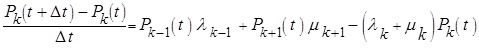 (10)
(10)
Переходя к пределу, получим дифференциальное уравнение для вероятности состояния 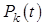 :
:
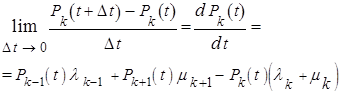 (11)
(11)
Рассчитанные значения установившихся вероятностей определяют искомые показатели качества системы. Обозначив 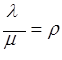 , где ρ – коэффициент загрузки, запишем выражения для предельных вероятностей состояний:
, где ρ – коэффициент загрузки, запишем выражения для предельных вероятностей состояний:
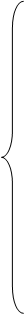
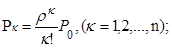
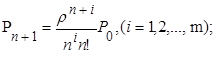 (12)
(12) 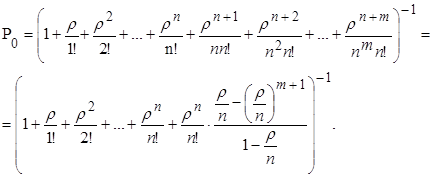
Здесь используется выражение для суммы геометрической прогрессии со знаменателем 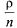 . Таким образом, все вероятности состояний найдены. Определим характеристики эффективности системы.
. Таким образом, все вероятности состояний найдены. Определим характеристики эффективности системы.
1) Вероятность отказа. Поступившая заявка получает отказ, если заняты n каналов и m мест в очереди:
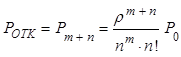 (13)
(13)
2) Относительная пропускная способность:
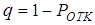 =1 -
=1 - 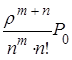 (14)
(14)
3) Абсолютная пропускная способность:
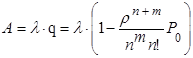 (15)
(15)
4) Среднее число занятых каналов.
Каждый занятый канал обслуживает в среднем 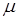 заявок в единицу времени. Вся СМО обслуживает в единицу времени A заявок, поэтому среднее число занятых каналов определится так:
заявок в единицу времени. Вся СМО обслуживает в единицу времени A заявок, поэтому среднее число занятых каналов определится так:
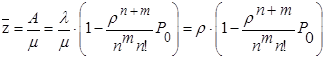 (16)
(16)
5) Среднее число заявок в очереди можно вычислить как математическое ожидание дискретной случайной величины:
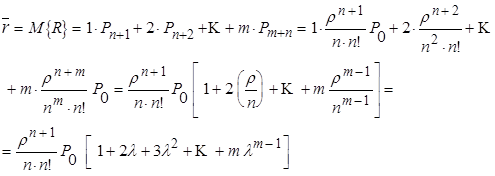 (17)
(17)
6) Среднее число заявок в системе:
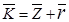 (18)
(18)
7) Среднее время ожидания заявки в очереди:
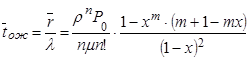 (19)
(19)
8) Среднее время пребывания заявки в системе:
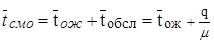 (20)
(20)
Таким образом, определив вероятности всех состояний СМО можно определить наиболее важные характеристики эффективности функционирования системы.
 2015-05-14
2015-05-14 261
261








