1. Инверсия (отрицание). Это отрицание любого высказывания, простым языком — «неверно» или «не», а в программировании это «Not». Обозначается как 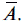
Таблица истинности для этой операции:
А B= не «А»
0 1
1 0
2. Операция КОНЪЮНКЦИЯ (логическое умножение). Конъюнкция — это составное высказывание, являющееся только тогда истинным, когда являются истинными простые высказывания, образующие это высказывание. На естественном языке обозначается союзом «и», в программировании как «And», а в записи логических функций это: & Можно записать одно и то же выражение по-разному, все варианты можно использовать в логических операциях:
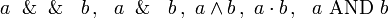
Таблица истинности для конъюнкции:
А B А & B
00 0
01 0
10 0
11 1
Например: Перемножить логически два числа в двоичной системе счисления.
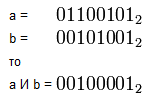
3. Операция ДИЗЪЮНКЦИЯ (логическое сложение). Дизъюнкция — это составное высказывание, являющееся только тогда истинным, когда хотя бы одно из образующих его высказываний является истинным.На естественном языке обозначается союзом «или», в программировании как «Or», а в записи логических функций как: V Также варианты записи:
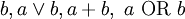
Таблица истинности для дизъюнкции:
А B А v B
00 0
01 1
10 1
11 1
Пример: Теперь сложить логически два числа побитно.
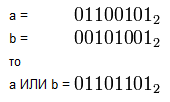
4. Операция ИМПЛИКАЦИЯ (логическое следование). Импликация — это составное высказывание, являющееся ложным тогда и только тогда, когда первое высказывание истинно, а второе высказывание ложно. Естественным языком можно сказать как «если…, то …», в программировании как «if», а в записи логических функций как: ⇒. Записываем так:
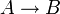 ...и это то же самое
...и это то же самое 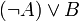
Для операции импликация будет верна следующая таблица истинности:
А B А → B
00 1
01 1
10 0
11 1
Для операции импликация можно рассмотреть еще частный случай: обратная импликация, таблица истинности которой ниже:
А B А ← B
00 1
01 0
10 1
11 1
5. Операция ЭКВИВАЛЕНЦИЯ (логическая равнозначность). Эквиваленция — это составное высказывание, являющееся истинным тогда и только тогда, когда все простые высказывания, образующие его, одновременно истинны или одновременно ложны. Естественным языком можно сказать как «тогда и только тогда», а в записи логических функций как: ⇔. Запишем так
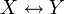
Для операции эквиваленция верна следующая таблица истинности:
А B А ↔ B
00 1
01 0
10 0
11 1
В конце можно привести пример, который может встретиться, например, в задании ЕГЭ:
«Для какого из указанных значений X истинно высказывание:
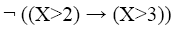
Варианты ответов: 1, 2, 3, 4.»
Решение в данном случае «лежит на поверхности»: действовать необходимо от обратного. Сначала, как видно из записи высказывания, идет операция отрицания, значит истинно высказывание будет тогда и только тогда, когда выражение под знаком отрицания будет ложным. Составное высказывание в скобках — это импликация из двух выражений сравнения. И, исходя из таблицы истинности импликации (см. п.4), значение «ложь» или «0», только когда первое высказывание (X>2) «истинно», а второе (X>3) «ложь». Из предложенных вариантов значений подходит только значение «3». Потому что подставляя его по значения X, получаем, что все высказывание ИСТИННО.
Ответ: 3.
 2015-05-14
2015-05-14 2034
2034
