Описание установки. Установка, реализующая метод, показана на рис.1

Установка, реализующая метод, показана на рис.1. Она состоит из сосуда А объёмом 10–12 литров, насоса С для закачки воздуха и манометрической U – образной трубки, в обеих коленах которой находится вода (рис.1). Соединение сосуда с окружающим воздухом осуществляется краном В.

До начала опыта краны В и Е (последний соединяет насос с сосудом) открыты.

Абсолютная температура воздуха в сосуде равна Т₀. Давление Р равна атмосферному Р ₀, таким образом параметры начального состояние Р₀,Т_{0 .}

В опыте создаются и анализируются следующие термодинамические состояния.

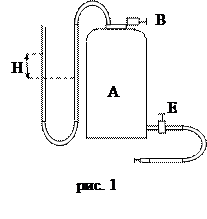
Состояние 1: кран В закрыт, кран Е открыт. С помощью насоса накачиваем воздух в сосуд. При этом давление и температура в сосуде повысится. Закрываем кран Е и ждём некоторое время, за которое произойдет теплообмен газа в сосуде с окружающей средой. В результате установится темпера Т₁=Т₀ и повышенное давление Р₁:

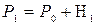(3)

где H₁– измеряемое на опыте давление столба воды, соответствующее давлению в сосуде. Так как в манометрической трубке отсчет высоты ведётся по линейной шкале от некоторого нулевого значения 00, то

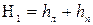
где h_л и h_п – расстояние от 00 до мениска жидкости соответственно в правом и левом колене трубки (рис.1). Параметры состояния равны Р₁,Т_{0 .}

Состояние 2. Кран Е закрыт, кран В быстро открывается. При этом воздух в сосуде адиабатически расширяется и давление достигает Р₀. За это время воздух охлаждается до температуры Т₂. Параметры состояния равны Р₀,Т_{2 .}

Состояние 3. Кран В после открытия столь же быстро закрывается; давление внутри сосуда начинает возрастать, т.к. охладившийся при адиабатном расширении воздух в сосуде вновь нагревается. Когда температура сравняется с температурой окружающего сосуд воздуха Т₃=Т₀, возрастает давление прекратится, достигнув некоторого значения

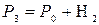(4)

Параметры состояние 3 равны Р₃,Т₀.

Итак, при переходе из 1 состояния во 2 происходит адиабатное расширение, подчиняющейся закону Пуассона (1), которое запишем в форме 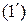. С учётом выражения (3) получаем:

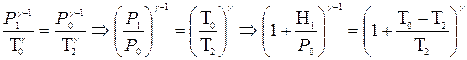(5)

Переход из состояния 2 в 3 происходит при постоянном объёме, т.е. согласно закону Гей– Люссака:

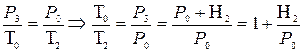(6)

В уравнении (5) величина 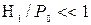и (Т₀–Т₂)/Т₂<<1

Логарифмируя левую и правую части уравнения и учитывая, что при малых 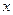справедливо приближенное равенство 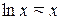, вместо (5)с учётом (6) получаем

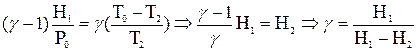(7)

Полученное уравнение позволяет определить значение γ по двум показаниям манометра (Η₁и Η₂).