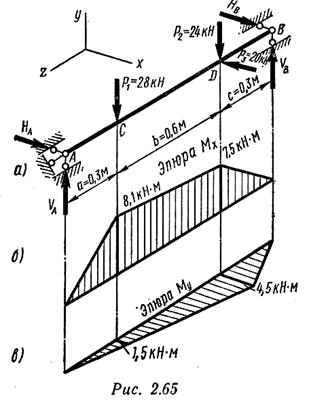
Решение. Определим опорные реакции от вертикальной

Определим опорные реакции от вертикальной

нагрузки:

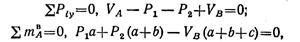
откуда

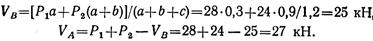
Составляем проверочное уравнение:

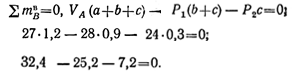Так как уравнение ΣM_B^в = 0 удовлетворяет­ся тождественно, то вертикальные реакции вычислены верно.

Составим уравнения равновесия в горизон­тальной плоскости:

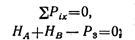
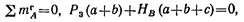
Откуда

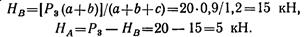
Составляем проверочное уравнение:

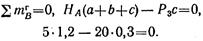
Уравнение обращается в тождество, значит реакции най­дены верно.

На рис. 2.65, б, в построены эпюры изгибающих мо­ментов соответственно в вертикальной М_х и горизонталь­ной М_у плоскостях. Определяем ординаты этих эпюр для характерных сечений:

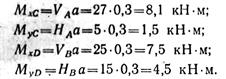
Результирующие изгибающие моменты в сечениях С и D составят:

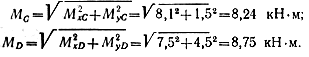
Опасным оказалось сечение D: в нем возникает наи­больший изгибающий момент. Составим для этого сече­ния условие прочности:

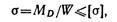
Откуда

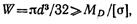
Или

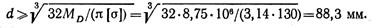
Принимаем d = 90 мм.

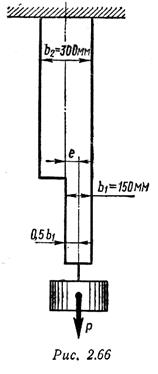
Пример 11. Ступенчатая сталь­ная полоса толщиной δ = 24 мм (рис. 2.66) поддерживает груз Р. Определить допускаемую величину силы Р по условию прочности поло­сы, если допускаемое напряжение для нее [ σ ] =160 Н/мм².

Решение

Нижняя ступень полосы нагружена центрально. Условие проч­ности для любого сечения этой сту­пени имеет вид:

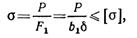
Откуда

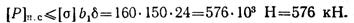
Верхняя ступень полосы испытывает внецентренное растяжение. Эксцентриситет приложения растягивающей силы Р (см. рис. 2.66)

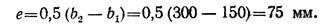
Условие прочности для любого сечения верхней ступени полосы имеет вид:

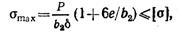
откуда

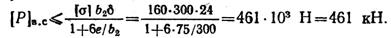
Очевидно, из двух найденных значений допускаемой величины силы Р следует принять меньшее, определяемое прочностью верхней сту­пени:

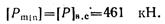
Приведенный пример показывает, что не всег­да увеличение сечения сопровождается возрастанием допускаемой на­грузки. В данном слу­чае как раз наоборот: вследствие появления эксцентриситета проч­ность верхней ступени полосы с большей пло­щадью сечения меньше, чем нижней ее ступени.

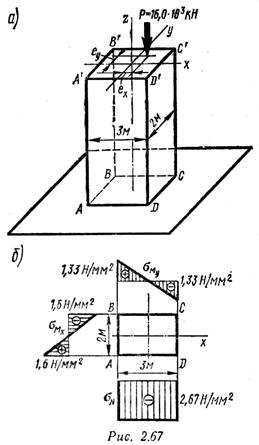Пример 12. Ка­менный столб нагружен силой Р = 16,0_*10³ кН (рис. 2.67, а). Опреде­лить, не учитывая мас­сы столба, наибольшее и наименьшее сжима­ющие напряжения в его подошве и указать точ­ки, где они возникают.