Задание 3. Решение задачи Коши для дифференциального уравнения в полных дифференциалах

Пример 1. Решить дифференциальное уравнение
(1+ 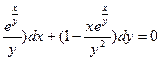, y(0) = 1.

Решение. Введем обозначения:

P(x,y):= 1 + 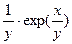, Q(x,y):= 1 - .

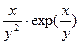Покажем, что уравнение является уравнением в полных дифференциалах:

→ ,

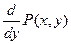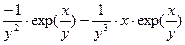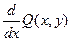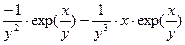→ , следовательно, = .

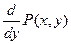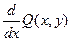Найдем частный интеграл уравнения:

u(x,y):= ,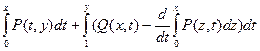

u(x,y) → x + exp(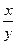) – 2 + y.

Проверим правильность решения, т. е. покажем, что u(x,y) = P(x,y)dx + Q(x,y)dy.

du(x,y,dx,dy):= (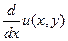)·dx + (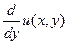)·dy,

du(x,y,dx,dy) – (P(x,y)·dx + Q(x,y)·dy) simplify → 0.

Проверим начальное условие u(0,1) → 0.

Частный интеграл имеет вид: x + exp(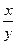) – 2 + y = 0.