2015-05-18
289
ARCH
Пусть временной ряд u_t представляет собой следующий процесс
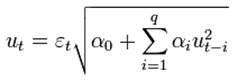
, где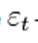 
- белый шум.
Тогда как условное, так и безусловное математическое ожидание этого процесса будет равно нулю. Условная дисперсия данного процесса будет равна
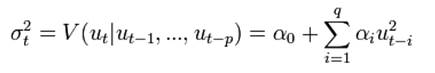
Такая модель условной дисперсии называется ARCH(q)-моделью. Для недопущения отрицательных значений дисперсии предполагается, что все коэффициенты модели неотрицательны, причем константа строго положительна. Если данный процесс стационарный, то безусловная дисперсия постоянна и равна, очевидно,
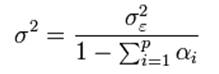
Необходимое условие стационарности — сумма коэффициентов модели (без константы) строго меньше единицы. Если сумма коэффициентов равна единице имеем интегрированный ARCH (нестационарный).
ARCH -процессы характеризуются положительным эксцессом («толстые хвосты»). Например, для ARCH(1)-процесса сдвиг от эксцесса нормального распределения равен 
Оценка параметров ARCH(q)-модели может быть произведена при помощи обычного МНК.
GARCH
ARCH-модель предполагает зависимость условной дисперсии только от квадратов прошлых значений временного ряда. Обобщить данную модель можно предположив, что условная дисперсия зависит также от прошлых значений самой условной дисперсии. Это так называемый обобщенный ARCH (Generalized ARCH — GARCH). В этом случае GARCH(p, q) модель (где p — порядок GARCH-членов σ2 и q — порядок ARCH-членов u2) описывается следующим образом:
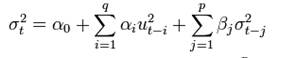
Необходимое условие стационарности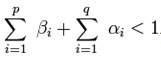 
Безусловная дисперсия стационарного GARCH(p, q)-процесса будет постоянна и равна
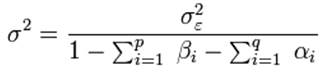
Если сумма коэффициентов равна единице, то имеем интегрированный GARCH — IGARCH, безусловная дисперсия которого бесконечна.
