Корреляционное отношение и индекс корреляции

Введенный выше коэффициент корреляции, как уже отме­чено, является полноценным показателем тесноты связи лишь в случае линейной зависимости между переменными. Однако час­то возникает необходимость в достоверном показателе интен­сивности связи при любой форме зависимости.

Для получения такого показателя вспомним правило сложе­ния дисперсий (8.12):

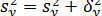, (3.37)

где 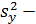общая дисперсия переменной

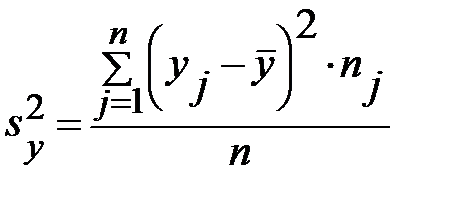, (3.38)

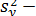средняя групповых дисперсий 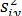, или остаточная дис­персия

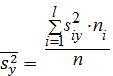, (3.39)

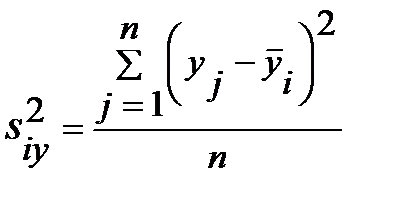, (3.40)

межгрупповая дисперсия

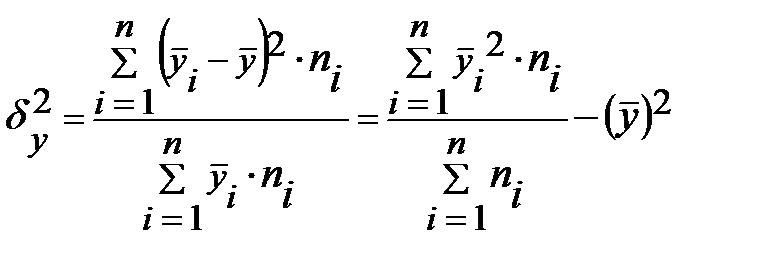. (3.41)

Остаточной дисперсией измеряют ту часть колеблемости Y, которая возникает из-за изменчивости неучтенных факторов, не зависящих от X. Межгрупповая дисперсия выражает ту часть вариации Y, которая обусловлена изменчивостью X. Величина

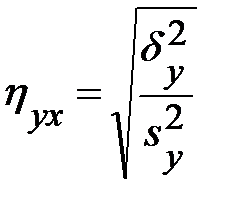(3.42)

получила название эмпирического корреляционного отношения Y поX. Чем теснее связь, тем большее влияние на вариацию пе­ременной Y оказывает изменчивость X по сравнению с неучтен­ными факторами, тем выше 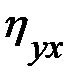. Величина 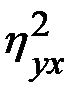, называемая эм­пирическим коэффициентом детерминации, показывает, какая часть общей вариации Y обусловлена вариацией X. Аналогично вводится эмпирическое корреляционное отношение X по Y.

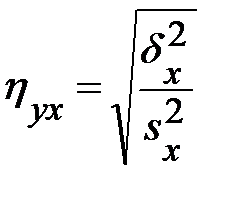. (3.43)

Отметим основные свойства корреляционных отношений (при достаточно большом объеме выборки n):

1. Корреляционное отношение есть неотрицательная величина,
не превосходящая .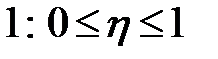

2. Если 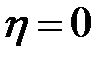,то корреляционная связь отсутствует.

3. Если 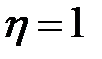, то между переменными существует функциональная зависимость.

4. 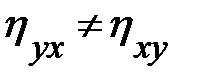, т.е. в отличие от коэффициента корреляции r (для которого 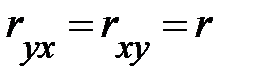) при вычислении корреляционного отношения существенно, какую переменную считать независи­мой, а какую — зависимой.

Эмпирическое корреляционное отношение 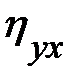является показа­телем рассеяния точек корреляционного поля относительно эмпири­ческой линии регрессии, выражаемой ломаной, соединяющей зна­чения 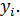Однако в связи с тем, что закономерное изменение 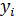нарушается случайными зигзагами ломаной, возникающими вследствие остаточного действия неучтенных факторов, 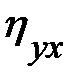преувеличивает тесноту связи. Поэтому наряду с 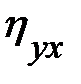рассматри­вается показатель тесноты связи 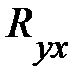характеризующий рассеяние точек корреляционного поля относительно линии регрессии 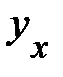(3.3). Показатель 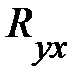получил название теоретического корреля­ционного отношения или индекса корреляции Y по X:

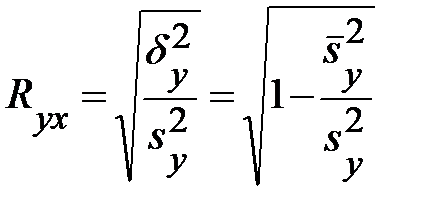. (3.44)

где дисперси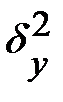и и 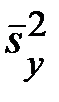определяются по формулам (12.54)— (12.56), в которых групповые средние 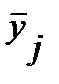заменены условными средними 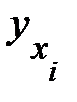, вычисленными по уравнению регрессии (12.16).

Подобно вводится и индекс корреляции X по Y:

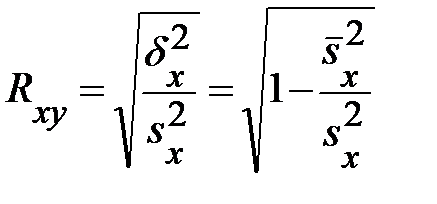. (3.45)

Достоинством рассмотренных показателей 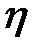и R является то, что они могут быть вычислены при любой форме связи меж­ду переменными. Хотя 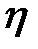и завышает тесноту связи по сравне­нию с R, но для его вычисления не нужно знать уравнение рег­рессии. Корреляционные отношения 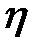и R связаны с коэффи­циентом корреляции r следующим образом:

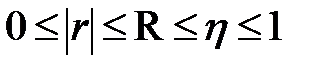. (3.46)

Коэффициент детерминации R², равный квадрату индекса корреляции (для парной линейной модели 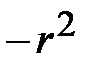), показывает долю общей вариации зависимой переменной, обусловленной регрес­сией или изменчивостью объясняющей переменной.

Чем ближе R² к единице, тем лучше регрессия аппроксими­рует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если R² = 1, то эмпирические точки (x, y) лежат на линии регрессии и между переменными YиX существует линейная функциональная зависимость. Если R² = 0, то вариация зависимой переменной полностью обуслов­лена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.

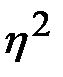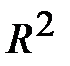Расхождение между и (или 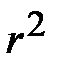) может быть использо­вано для проверки линейности корреляционной зави­симости.

Проверка значимости корреляционного отношения 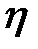осно­вана на том, что статистика

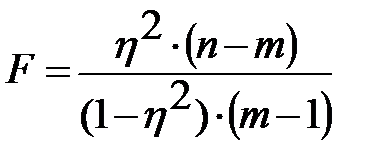(3.47)

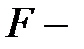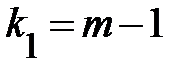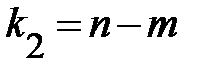име­ет распределение Фишера—Снедекора и степенями свободы. Поэтому 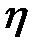значимо отличается от нуля, если 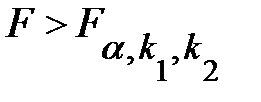, где 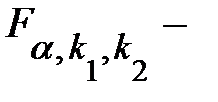табличное значение 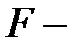критерия на уровне значимости 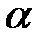при числе степеней свободы 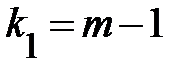и .

И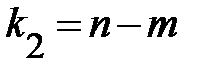ндекс корреляции R двух переменных значим, если значе­ние статистики

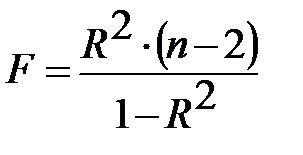(3.48)

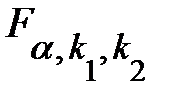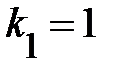больше табличного , где и .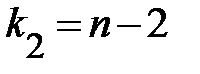

Пример 12.8. Рассмотрим в качестве примера зависимость между суточной выработкой продукции Y (т) и величиной основных производственных фондов (ОПФ) X (млн руб.) для совокупности 50 однотипных предприятий (12.1). По данным таблицы вычислить корреляционное отношение и индекс корреляции и проверить их значимость на уровне .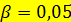

Таблица 12.1

Величина ОПФ, млн руб. (X)	Середины интервалов		Всего	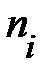Групповая средняя, т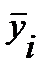
7-11	11-15	15-19	19-23	23-27
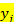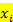20-25 25-30 30-35 35-40 40-45	22,5 27,5 32,5 37,5 42,5	- - -	-	-	- -	- - -		10,3 13,3 17,8 20,3 23,0
Всего	-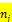
Групповая средняя 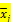, млн руб.	-	22,5	29,3	31,9	35,4	39,2	-	-

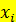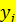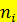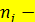В таблице через и обозначены середины соответствующих интервалов, а и соответственно их частоты.

В таблице групповые средние получены по формулам:

; .

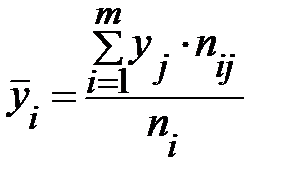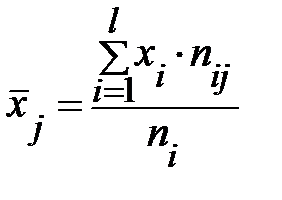Решение. По данным табл. 12.1 на первом этапе вычислим общую среднюю признака y, для этого воспользуемся формулой:

.

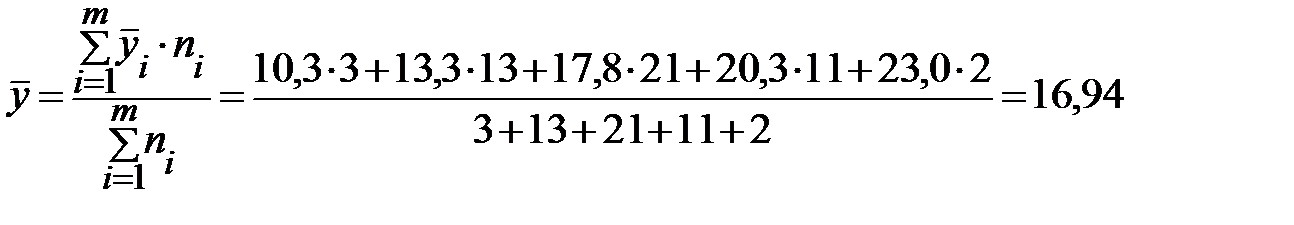Для вычисления общей дисперсии воспользуемся известной формулой:

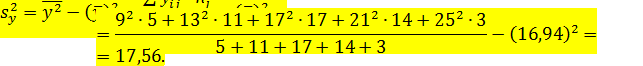
Межгрупповую дисперсию получим по формуле (12.57):

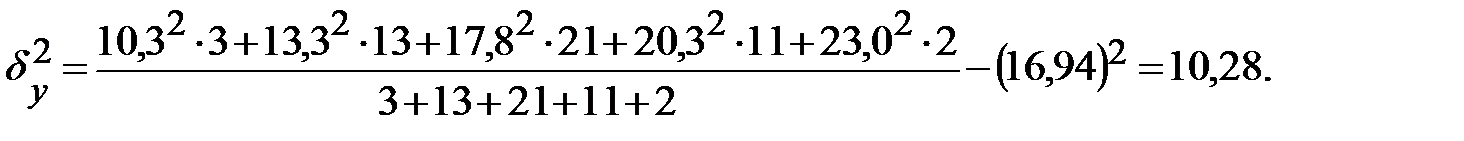
Эмпирическое корреляци­онное отношение получим по формуле (1.58):

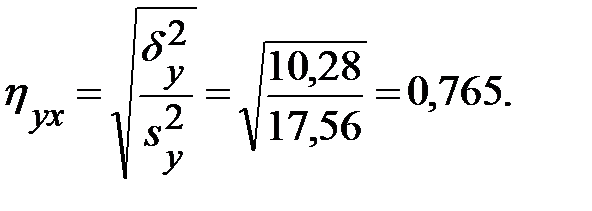
Теперь по (12.57) 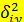=517,8/50 = 10,36 и по (12.58)

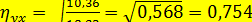. Значение 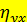близко к величине 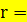0,740 (полученной ранее в примере 12.3). Поэтому оправда­но сделанное выше на основании графического изображения эмпирической линии (ломаной) регрессии предположение о ли­нейной корреляционной зависимости между переменными.

Для расчета 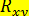по уравнению регрессии 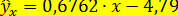(см. пример 12.1) находим значения 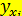, представленные в пред­последней графе табл. 12.4. Затем аналогично 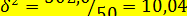и 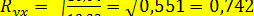. Как и следовало ожидать, 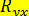оказался равным (небольшое расхождение объясняет­ся округлением промежуточных результатов при вычислении 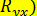. Поэтому в случае линейной связи нет смысла вычислять 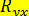, а достаточно ограничиться вычислением . Величина коэф­фициента детерминации 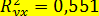показывает, что вариация зависимой переменной Y (суточной выработки продукции) на 55,1% объясняется вариацией независимой переменной Х (величиной основных производственных фондов).

Для проверки значимости 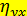, учитывая, что количество интервалов по группировочному признаку , по (12.63)

.

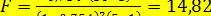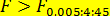Табличное значение . Так как , то 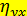значимо отличается от нуля. Аналогично проверяется значимость найдем 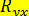. По (12.64) . Так как 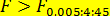, то индекс корреляции 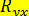значим.

3 .8. Множественный регрессионный анализ

Экономические явления, как правило, определяются боль­шим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимо­сти одной зависимой переменной Y от нескольких объясняющих переменных 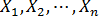. Эта задача решается с помощью множе­ственного регрессионного анализа.

Множественное линейное уравнение регрессии имеет вид:

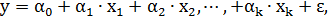(3.49)

где 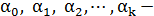неизвестные параметры модели; 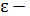случайная ошибка модели, обусловленная влиянием неучтенных факторов в модель, а также случайными ошибками наблюдении.

Для определения неизвестных параметров модели множественной регрессии из генеральных совокупностей сформированы две выборки объемами n:

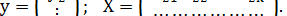
Подставляя эти выборки в модель регрессии (3.49) получим систему уравнении множественной линейной регрессии:

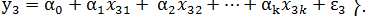(3.50)

Включение в регрессионную модель новых объясняющих пе­ременных (факторов) усложняет получаемые формулы и вычисления. Это приводит к целесообразности использования матричных обозначе­ний. Матричное описание регрессии облегчает как теоретические концепции анализа, так и необходимые расчетные процедуры.

Введем обозначения: 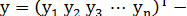вектор столбец, значений зависимой переменной размера n;

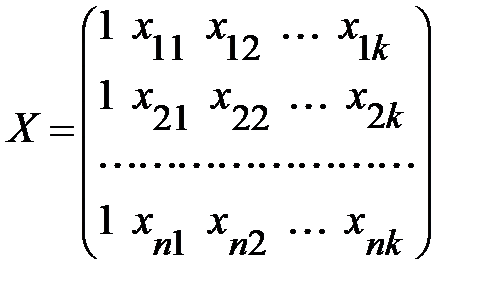
— матрица значений объясняющих переменных, или матрица плана размера ;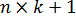

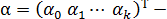вектор столбец, параметров размера (k+1);

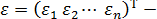вектор столбец, возмущений (случайных ошибок, остатков) размера п.

Тогда в матричной форме модель (3.50) примет вид:

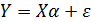. (3.51)

Оценкой этой модели по выборке является уравнение

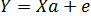, (3.52)

где , .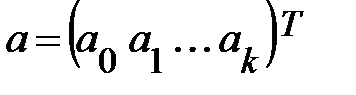

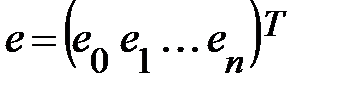Для оценки вектора неизвестных параметров 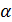применим метод наименьших квадратов. Так как произведение транспони­рованной матрицы 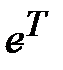на саму матрицу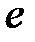

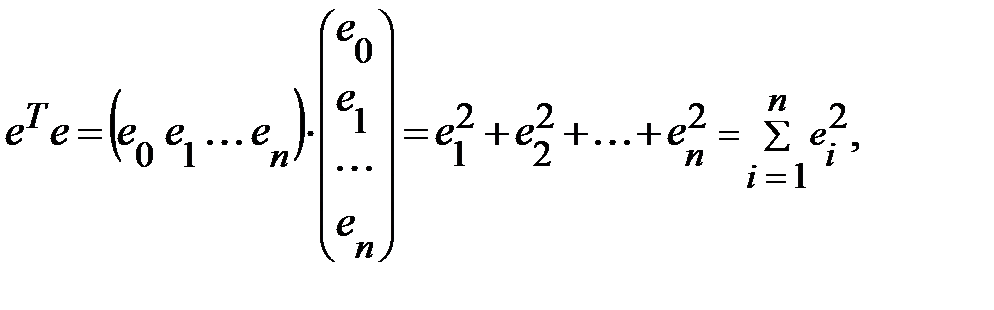
то условие минимизации остаточной суммы квадратов запишет­ся в виде:

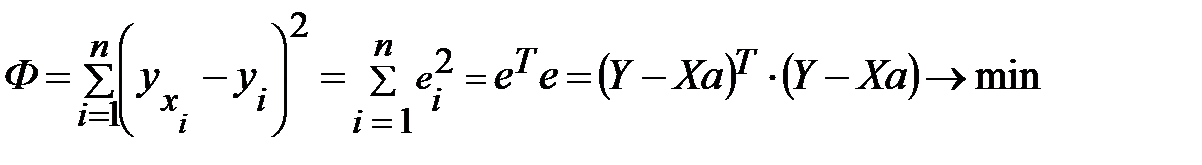. (3.53)

Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, т.е. 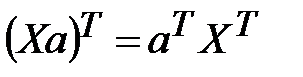, получим после раскрытия ско­бок:

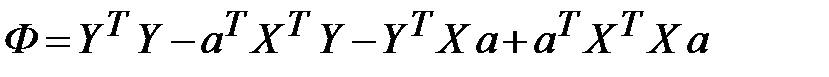. (3.54)

Произведение 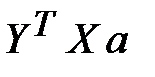есть матрица размера 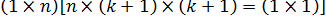, т.е. величина скалярная, следовательно, оно не меняется при транспонировании: 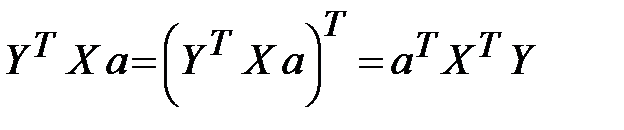. По­этому условие минимизации (3.54) примет вид:

.

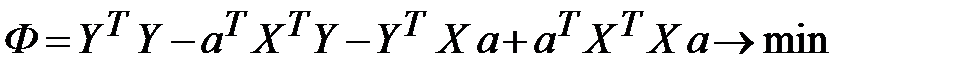На основании необходимого условия экстремума функции не­скольких переменных 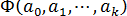, представляющей (3.55), необ­ходимо приравнять к нулю частные производные по этим пере­менным или в матричной форме — вектор частных производных

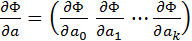. (3.55)

Таким образом, встает задача найти минимум этой функций. Для этого выражение (3.55) следует продифференцировать по векторному аргументу 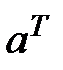и полученное выражение приравнять к нулю, то есть:

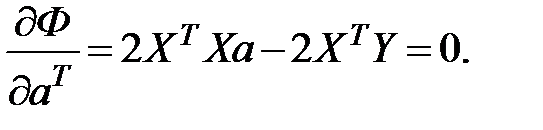
Отсюда получается следующее выражение:

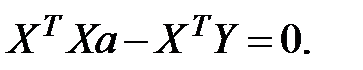
Данная система уравнений называется нормальной системой уравнений регрессии. Требуется ввести обозначения: 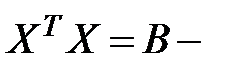матрица коэффициентов нормальных уравнений, 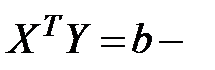вектор-столбец свободных членов нормальных уравнений регрессии.

С учетом введенных обозначений нормальная система уравнений регрессии перепишется в окончательном виде:

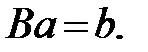(3.56)

Для решения матричного уравнения (3.56) относительно вектора оценок параметров 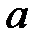необходимо ввести пред­посылку для множественного регрессионного анализа: матрица 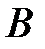является неособенной, т.е. ее определитель не равен нулю. Следовательно, ранг матрицы 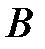равен ее порядку, т.е. 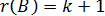. Из матричной алгебры известно, что 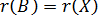, значит, 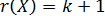, т.е. ранг матрицы плана 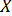равен числу ее столбцов.

Кроме того, полагают, что число имеющихся наблюдений (значений) каждой из объясняющих переменных превосходит ранг матрицы 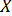, т.е. 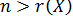или 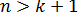, ибо в противном случае в принципе невозможно получение сколько-нибудь на­дежных статистических выводов.

Если матрица коэффициентов нормальных уравнений 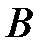хорошо обусловлена и обратима, то можно получить решение системы (3.56), например, в виде:

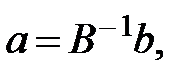(3.57)

где 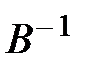- обратная матрица, соответствующая условиям:

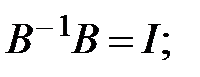
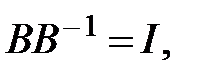
где 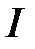- единичная матрица соответствующих размеров.

Зная вектор 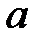, модель уравнения множественной рег­рессии можно представить в виде:

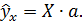(3.58)

Преобразуем вектор оценок (13.26) с учетом (13.23) получим:

,

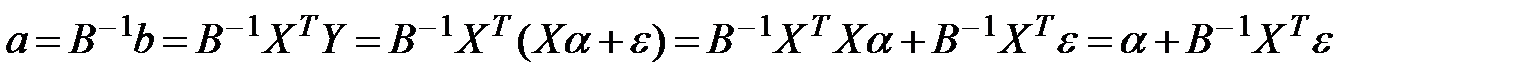Откуда

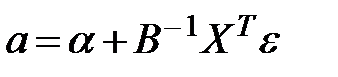, (3.59)

т. е. оценки параметров (3.59), найденные по выборке, будут содержать случайные ошибки.

Пример 13.4. Имеются следующие данные (условные) о сменной добыче угля на одного рабочего Y(t), мощности пласта Х\ (м) и уровне механизации работ Х₂ (%), характеризующие процесс добычи угля в 10 шахтах.

Таблица 13.6

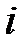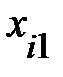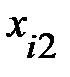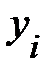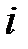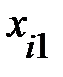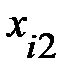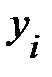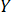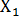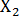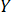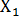Предполагая, что между переменными , и существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии , по и .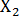

Решение. Обозначим

, ,

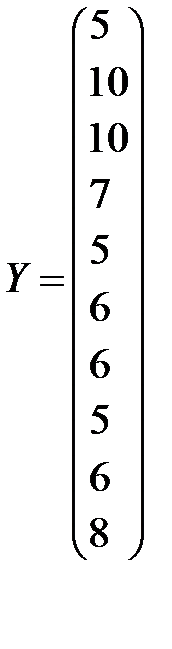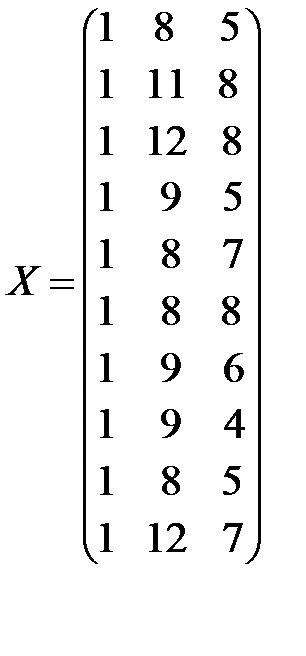(напоминаем, что в матрицу плана X вводится дополнительный столбец чисел, состоящий из единиц).

Решение системы уравнении найдем методом псевдонормального решения:

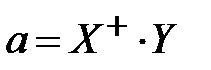, (3.60)

где 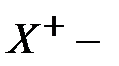псевдообратная матрица к исходной матрице .

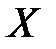Псевдообратную матрицу найдем по рекурсивному алгоритму (№№№) и она равна:

Тогда по формуле (13.29) найдем вектор столбец параметров регрессии:

.

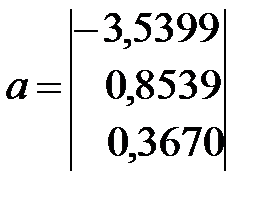С учетом (13.27) уравнение множественной регрессии имеет вид:

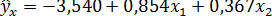. (13.30)

Уравнение множественной регрессии (13.30) показывает, что при увели­чении только мощности пласта 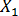(при неизменном 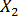) на 1 м, добыча угля на одного рабочего Y увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ 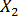на 1% (при неизменной 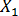) в среднем на 0,367 т.

Добавление в регрессионную модель новой объясняющей переменной 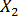изменило коэффициент регрессии 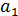(Y по 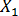) с 1,016 для парной регрессии (см. пример 13.1) до 0,854 — для множественной регрессии. В этом никакого противоречия нет, так как во втором случае коэффициент регрессии позволяет оценить прирост зависимой переменной Y при изменении на единицу объясняющей переменной 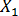в чистом виде, независи­мо от 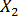. В случае парной регрессии 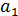учитывает воздействие на Y не только переменной 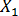, но и косвенно корреляционно связанной с ней переменной . ►

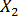На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии 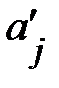и коэффициенты эластичности :

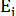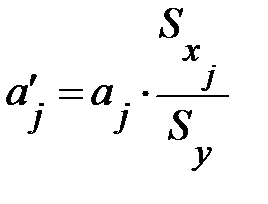. (13.31)

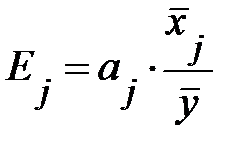. (13.32)

Стандартизованный коэффициент регрессии 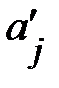показывает, на сколько величин 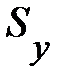изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на 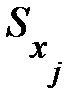, а коэффици­ент эластичности 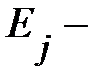на сколько процентов (от средней) изме­нится в среднем Y при увеличении только 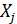на 1%.

4.9. Ковариационная матрица и ее выборочная оценка

Вариации оценок параметров будут, в конечном счете, опре­делять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматрива­ют так называемую ковариационную матрицу К, являющуюся матричным аналогом дисперсии одной переменной:

.

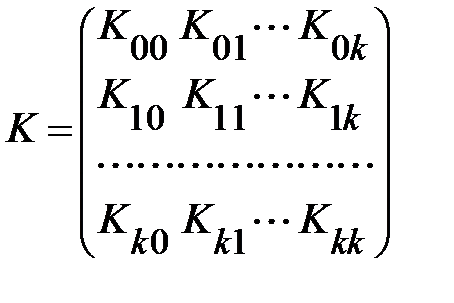где элементы 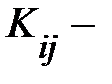ковариации (или корреляционные моменты) оце­нок параметров 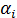и 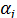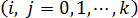. Ковариация двух пере­менных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий [Ссылка]. Поэтому

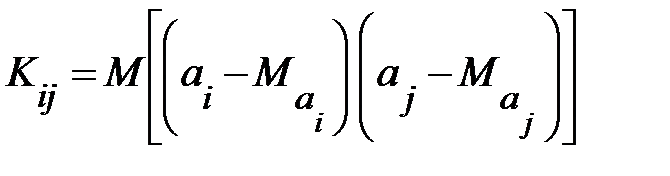, (13.28)

где 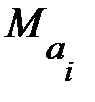и 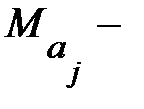математические ожидания соответственно для параметров 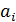и .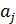

Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.

В силу того, что оценки 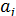, полученные методом наименьших квадратов, являются несмещенными оценками параметров 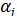, т.е. 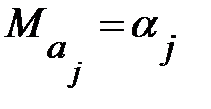, выражение (13.28) примет вид:

.

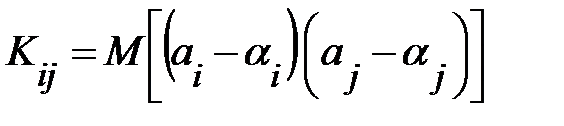Рассматривая ковариационную матрицу К, легко заметить, что на ее главной диагонали находятся дисперсии опенок пара­метров регрессии, ибо

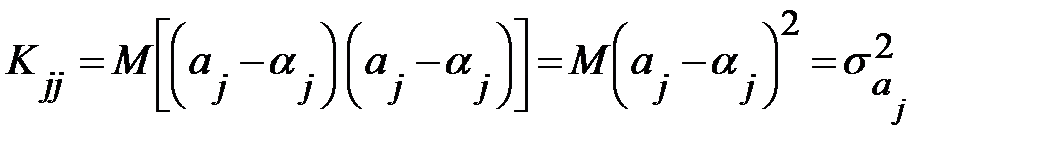. (13.29)

В сокращенном виде ковариационная матрица К имеет вид:

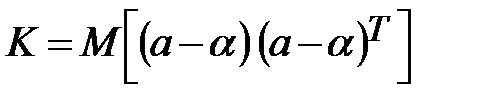. (13.30)

Учитывая (13.28) мы можем записать

.

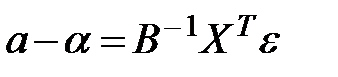Тогда выражение (12.30) примет вид:

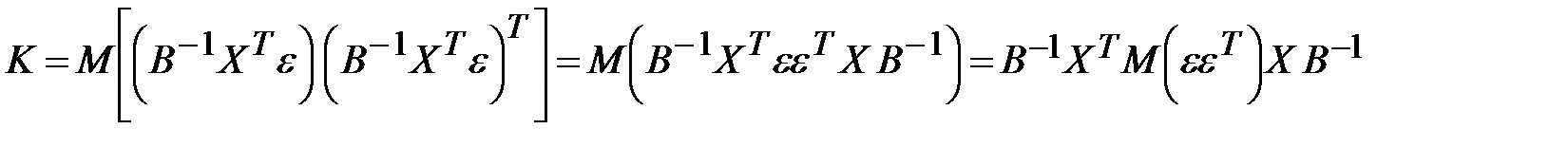, (13.31)

ибо элементы матрицы X —неслучайные величины.

Матрица 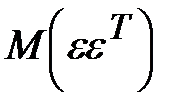представляет собой ковариационную матри­цу вектора возмущений :

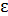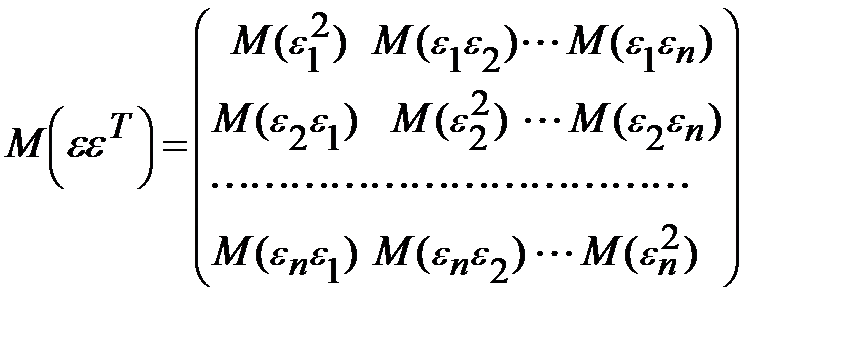
в которой все элементы, не лежащие на главной диагонали, равны нулю в силу предпосылки 4 о некоррелированности воз­мущени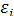й , и 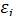между собой, а все элементы, ле­жащие на главной диагонали, в силу предпосылок 2 и 3 регрес­сионного анализа равны одной и той же дисперсии :

.

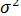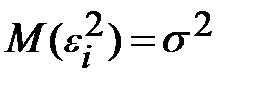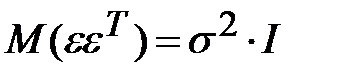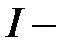Поэтому матрица , где единичная матрица 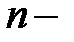го

порядка. Следовательно, в силу (13.31) ковариационная матрица вектора 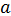оценок параметров:

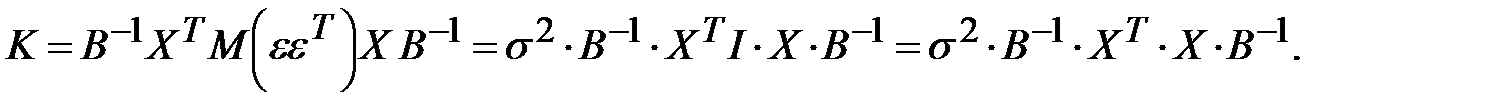
Так как 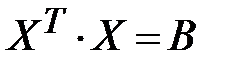и 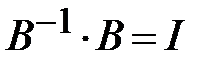, то окончательно получим:

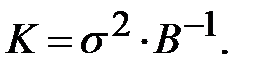(13.32)

Таким образом, с помощью обратной матрицы 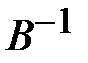нормальных уравнении регрессииопределяется не только сам вектор 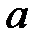оценок параметров (13.28), но и дисперсии и ковариации его компонент.

Входящая в (13.32) дисперсия возмущений неизвестна. За­менив ее выборочной остаточной дисперсией

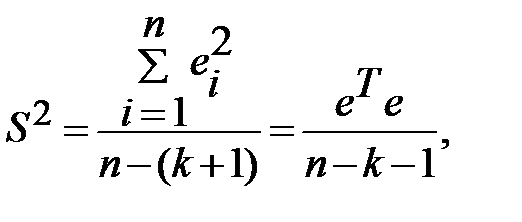(13.33)

по (13.32) получаем выборочную оценку ковариационной мат­рицы К. (В знаменателе выражения (13.33) стоит 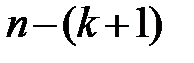, а не 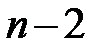, как это было выше в (13.6). Это связано с тем, что теперь 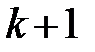степеней свободы (а не две) теряются при определении не­известных параметров, число которых вместе со свободным чле­ном 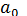равно .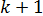

4.10. Определение доверительных интервалов

для коэффициентов и функции множественной регрессии

Перейдем теперь к оценке значимости коэффициентов рег­рессии 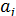и построению доверительного интервала для парамет­ров регрессионной модели .

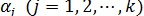В силу (13.29), (13.32) и изложенного выше оценка диспер­сии коэффициента регрессии 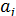определится по формуле:

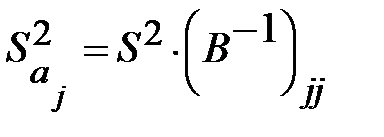
где 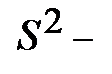несмещенная оценка параметра ;

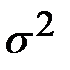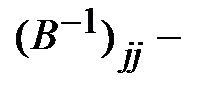диагональный элемент матрицы .

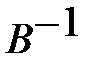Среднее квадратическое отклонение (стандартная ошибка) коэффициента регрессии 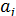примет вид:

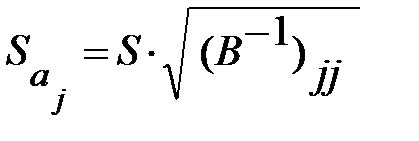. (13.34)

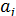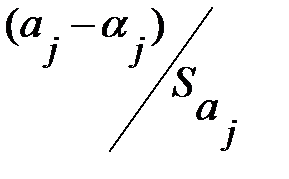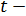Значимость коэффициента регрессии можно проверить, если учесть, что статистика имеет распределение Стьюдента с

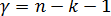степенями свободы. Поэтому 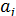значимо отли­чается от нуля на уровне значимости 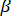, если 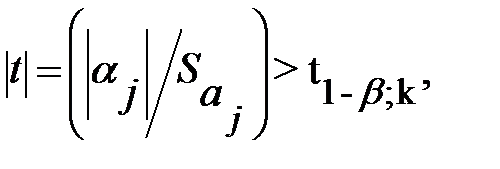соответствующий 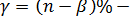ный дове­рительный интервал для параметра 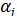есть

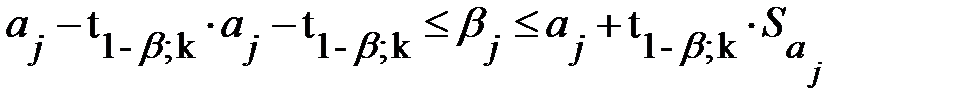. (13.35)

Наряду с интервальным оцениванием коэффициентов рег­рессии по (13.35) весьма важным для оценки точности опреде­ления зависимой переменной (прогноза) является построение доверительного интервала для функции регрессии или для условно­го математического ожидания зависимой переменной 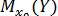, найден­ного в предположении, что объясняющие переменные 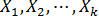приняли значения, задаваемые вектором

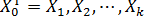.Выше такой интервал получен для уравнения парной регрессии (см. (13.13) и (13.12)). Обобщая соответствующие выражения на случай множественной регрессии, можно получить доверитель­ный интервал для :

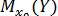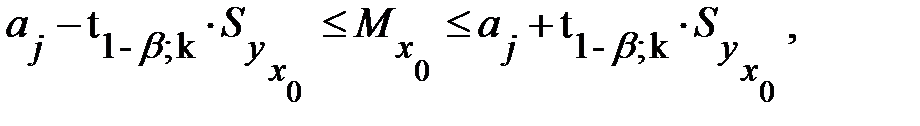
где 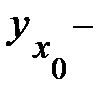групповая средняя, определяемая по уравнению рег­рессии,

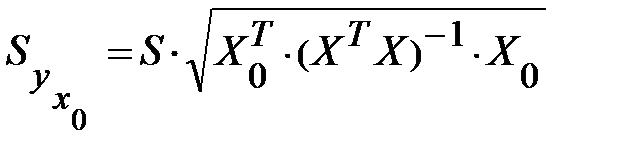(13.36)

— ее стандартная ошибка.

При обобщении формул (13.15) и (13.14) аналогичный дове­рительный интервал для индивидуальных значений зависимой пе­ременной 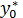примет вид:

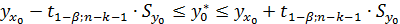(13.37)

где

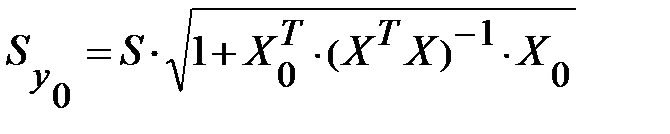. (13.38)

Доверительный интервал для дисперсии возмущений 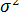в мно­жественной регрессии с надежностью 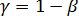строится анало­гично парной модели по формуле (13.20) с соответствующим изменением числа степеней свободы критерия :

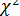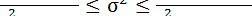(13.39)

Пример 13.6. По данным примера 13.4 оценить сменную добычу угля на одного рабочего для шахт с мощностью пласта 8 м и уровнем механизации работ 6%; найти 95%-ные доверитель­ные интервалы для индивидуального и среднего значений смен­ной добычи угля на 1 рабочего для таких же шахт. Проверить значимость коэффициентов регрессии и построить для них 95%-ные доверительные интервалы. Найти с надежностью 0,95 ин­тервальную оценку для дисперсии возмущений .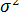

Решение. В примере 13.4 уравнение регрессии получено в виде:

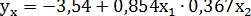. По условию надо оценить 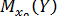, где 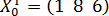. Выборочной оценкой 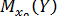, является групповая средняя, которую найдем по уравнению регрессии: 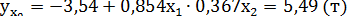. Для построения до­верительного интервала для М (у) необходимо знать дисперсию его оценки 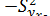. Для ее вычисления обратимся к табл. 13.7 (точнее к ее двум последним столбцам, при составлении кото­рых учтено, что групповые средние определяются по получен­ному уравнению регрессии).

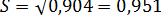Теперь по (13.37): и (т).

Определяем стандартную ошибку групповой средней г> по формуле (13.41). Вначале найдем

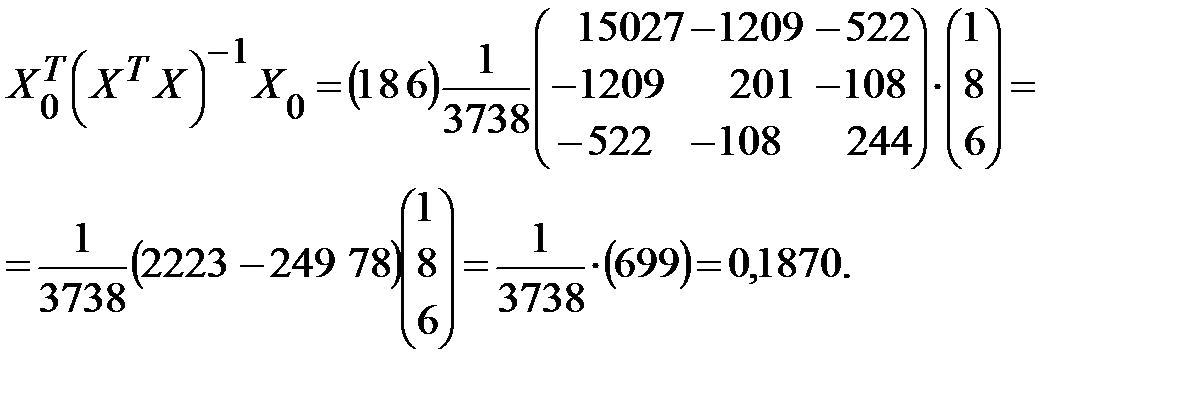
Теперь 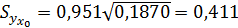(т).

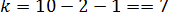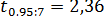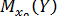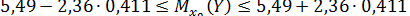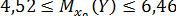По табл. IV приложений при числе степеней свободы находим . По (13.40) доверительный интервал для , равен или (т).

Итак, с надежностью 0,95 средняя сменная добыча угля на одного рабочего для шахт с мощностью пласта 8 м и уровнем механизации работ 6% находится в пределах от 4,52 до 6,46 т.

Сравнивая новый доверительный интервал для функции рег­рессии 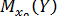, полученный с учетом двух объясняющих пере­менных, с аналогичным интервалом с учетом одной объясняю­щей переменной (см. пример 13.1), можно заметить уменьшение его величины. Это связано с тем, что включение в модель новой объясняющей переменной позволяет несколько повысить точ­ность модели за счет увеличения взаимосвязи зависимой и объ­ясняющей переменных (см. ниже).

Найдем доверительный интервал для индивидуального зна­чения 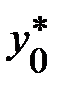при

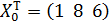по (13.43): 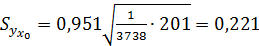(т) и по (13.42): 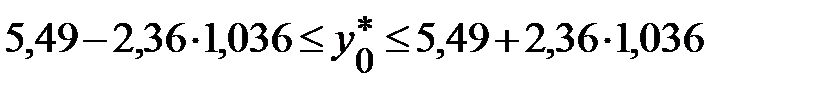, т. е. 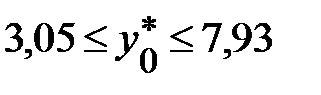(т).

Итак, с надежностью 0,95 индивидуальное значение сменной добычи угля в шахтах с мощностью пласта 8 м и уровнем меха­низации работ 6% находится в пределах от 3,05 до 7,93 (т).

Проверим значимость коэффициентов регресси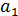и и 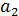. В примере 13.4 получены 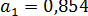и 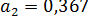. Стандартная ошибка 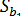в соответствии с (13.38) равна: 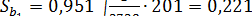. Так как 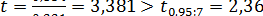, то коэффициент 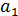значим. Аналогично вычисляем 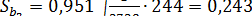и 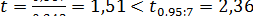т.е. коэффициент 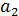незначим на 5%-ном уровне.

Доверительный интервал имеет смысл построить только для значимого коэффициента регрессии 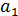: по (13.39) 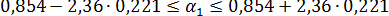или .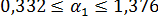

Итак, с надежностью 0,95 за счет изменения на 1 м мощности пласта 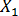(при неизменном 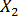) сменная добыча угля на одного рабочего У будет изменяться в пределах от 0,332 до 1,376 т.

Найдем 95%-ный доверительный интервал для параметра ст². Учитывая, что 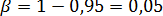, , 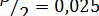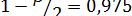найдем по табл. V приложений при 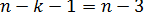степенях свободы 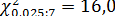; 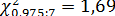и по формуле (13.43')

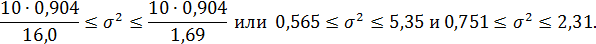
Таким образом, с надежностью 0,95 дисперсия возмущений заключена в пределах от 0,565 до 5,35, а их стандартное откло­нение — от 0,751 до 2,31 (т).

Формально переменные, имеющие незначимые коэффици­енты регрессии, могут быть исключены из рассмотрения. В эко­номических исследованиях исключению переменных из регрес­сии должен предшествовать тщательный качественный анализ. Поэтому может оказаться целесообразным все же оставить в регрессионной модели одну или несколько объясняющих пере­менных, не оказывающих существенного (значимого) влияния на зависимую переменную.

4.11. Мультиколлинеарность

Под мульттоллинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеар­ность может проявляться в функциональной (явной) и стохасти­ческой (скрытой) формах.

При функциональной форме мультиколлинеарности по край­ней мере одна из парных связей между объясняющими пере­менными является линейной функциональной зависимостью. В этом случае матрица 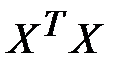особенная, так как содержит линей­но зависимые векторы-столбцы и ее определитель равен нулю, т.е. нарушается предпосылка 6 регрессионного анализа. Это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели.

Однако в экономических исследованиях мультиколлинеар­ность чаще проявляется в стохастической форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Матрица 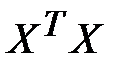в этом случае является неособенной, но ее определитель очень мал. В то же время век­тор оценок 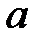и его ковариационная матрица К в соответствии с формулами (13.28) и (13.36) пропорциональны обратной матри­це 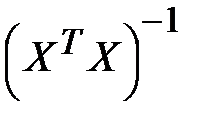а значит, их элементы обратно пропорциональны величине определителя 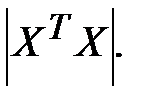В результате получаются значи­тельные средние квадратические отклонения (стандартные ошибки) коэффициентов регрессии 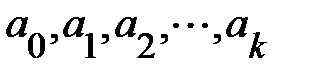и оценка их зна­чимости по 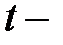критерию не имеет смысла, хотя в целом регрес­сионная модель может оказаться значимой по 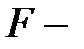критерию.

Оценки 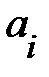становятся очень чувствительными к незначитель­ному изменению результатов наблюдений и объема выборки. Уравнения регрессии в этом случае, как правило, не имеют ре­ального смысла, так как некоторые из его коэффициентов могут иметь неправильные с точки зрения экономической теории зна­ки и неоправданно большие значения.

Один из методов выявления мультиколлинеарности заключа­ется в анализе корреляционной матрицы между объясняющими переменными 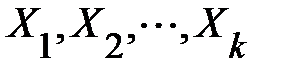и выявлении пар переменных, имею­щих высокие коэффициенты корреляции (обычно больше 0,8). Ес­ли такие переменные существуют, то говорят о мультиколлине­арности между ними.

Полезно также находить множественные коэффициенты корреляции между одной из объясняющих переменных и неко­торой группой из них. Наличие высокого множественного ко­эффициента корреляции (обычно принимают больше 0,8) сви­детельствует о мультиколлинеарности.

Другой подход состоит в исследовании матрицы 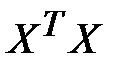. Если определитель матрицы 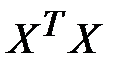близок к нулю (например, одного порядка с накапливающимися ошибками вычислений), то это говорит о наличии мультиколлинеарности.

Для устранения или уменьшения мультиколлинеарности ис­пользуется ряд методов. Один из них заключается в том, что из двух объясняющих переменных, имеющих высокий коэффици­ент корреляции (больше 0,8), одну переменную исключают из рассмотрения. При этом, какую переменную оставить, а какую удалить из анализа, решают в первую очередь на основании экономических соображений. Если с экономической точки зре­ния ни одной из переменных нельзя отдать предпочтение, то оставляют ту из двух переменных, которая имеет больший ко­эффициент корреляции с зависимой переменной.

Другим из возможных методов устранения или уменьшения мультиколлинеарности является использование пошаговых про­цедур отбора наиболее информативных переменных. Например, вначале рассматривается линейная регрессия зависимой пере­менной Кот объясняющей переменной, имеющей с ней наибо­лее высокий коэффициент корреляции (или индекс корреляции при нелинейной форме связи). На втором шаге включается в рассмотрение та объясняющая переменная, которая имеет наи­более высокий частный коэффициент корреляции с Y и вычис­ляется множественный коэффициент (индекс) корреляции. На третьем шаге вводится новая объясняющая переменная, которая имеет наибольший частный коэффициент корреляции с Y, и вновь вычисляется множественный коэффициент корреляции и т.д.

Процедура введения новых переменных продолжается до тех пор, пока добавление следующей объясняющей переменной суще­ственно не увеличивает множественный коэффициент корреляции.