Тема 5. Модели прогнозирования экономических процессов

5.7. Трендовые модели на основе кривых роста

Основная цель создания трендовых моделей экономиче­ской динамики — на их основе сделать прогноз о развитии изучаемого процесса на предстоящий промежуток времени. Прогнозирование на основе временного ряда экономических показателей относится к одномерным методам прогнозиро­вания, базирующимся на экстраполяции, т.е. на продлении на будущее тенденции, наблюдавшейся в прошлом. При та­ком подходе предполагается, что прогнозируемый показа­тель формируется под воздействием большого количества факторов, выделить которые либо невозможно, либо по кото­рым отсутствует информация. В этом случае ход изменения данного показателя связывают не с факторами, а с течением времени, что проявляется в образовании одномерных вре­менных рядов. Рассмотрим метод экстраполяции на основе так называемых кривых роста экономической динамики.

Использование метода экстраполяции на основе кривых роста для прогнозирования базируется на двух предположе­ниях:

• временной ряд экономического показателя действитель­но имеет тренд, т.е. преобладающую тенденцию;

• общие условия, определявшие развитие показателя в прошлом, останутся без существенных изменений в тече­ние периода упреждения.

В настоящее время насчитывается большое количество типов кривых роста для экономических процессов. Чтобы правильно подобрать наилучшую кривую роста для модели­рования и прогнозирования экономического явления, необ­ходимо знать особенности каждого вида кривых. Наиболее часто в экономике используются полиномиальные, экспо­ненциальные и S-образные кривые роста. Простейшие поли­номиальные кривые роста имеют вид:

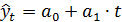(полином первой степени)

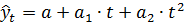(полином второй степени)

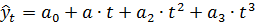(полином третьей степени)

и т.д.

Параметр 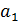называют линейным приростом, параметр 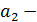ускорением роста, параметр 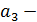изменением ускоре­ния роста.

Для полинома первой степени характерен постоянный закон роста. Если рассчитать первые приросты по формуле 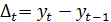, ,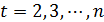то они будут постоянной вели­чиной и равны .

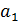Если первые приросты рассчитать для полинома второй степени, то они будут иметь линейную зависимость от вре­мени и ряд из первых приростов 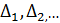на графике будет представлен прямой линией. Вторые приросты 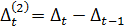для полинома второй степени будут постоянны.

Для полинома третьей степени первые приросты будут полиномами второй степени, вторые приросты будут линейной функцией времени, а третьи приросты, рассчитываемые по формуле 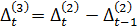, будут постоянной величиной.

На основе сказанного можно отметить следующие свойст­ва полиномиальных кривых роста:

• от полинома высокого порядка можно путем расчета последовательных разностей (приростов) перейти к поли­ному более низкого порядка;

• значения приростов для полиномов любого порядка не зависят от значений самой функции .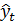

Таким образом, полиномиальные кривые роста можно использовать для аппроксимации (приближения) и прогно­зирования экономических процессов, в которых последую­щее развитие не зависит от достигнутого уровня.

В отличие от использования полиномиальных кривых использование экспоненциальных кривых роста предпола­гает, что дальнейшее развитие зависит от достигнутого уров­ня, например, прирост зависит от значения функции. В эко­номике чаще всего применяются две разновидности экспо­ненциальных (показательных) кривых: простая экспонента и модифицированная экспонента.

Простая экспонента представляется в виде функции

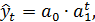(5.1)

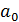где и 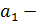положительные числа, при этом если 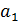больше единицы, то функция возрастает с ростом времен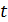и ,если 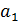меньше единицы — функция убывает.

Можно заметить, что ордината данной функции изме­няется с постоянным темпом прироста. Если взять отно­шение прироста к самой ординате, оно будет постоянной величиной:

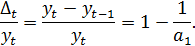
Прологарифмируем выражение для данной функции по любому основанию:

.

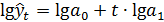Отсюда можно заметить, что логарифмы ординат простой экспоненты линейно зависят от времени.

Модифицированная экспонента имеет вид

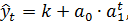(5.2)

где постоянные величины: 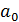.меньше нуля, 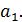положительна и меньше единицы, а константа 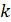носит название асимптоты этой функции, т.е. значения функции неограниченно при­ближаются (снизу) к величине 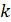.Могут быть другие варианты модифицированной экспоненты, но на практике наиболее часто встречается указанная выше функция.

Если прологарифмировать первые приросты данной функ­ции, то получится функция, линейно зависящая от времени, а если взять отношение двух последовательных приростов, то оно будет постоянной величиной:

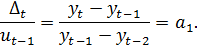
В экономике достаточно распространены процессы, кото­рые сначала растут медленно, затем ускоряются, а затем снова замедляют свой рост, стремясь к какому-либо пределу. В качестве примера можно привести процесс ввода некоторого объекта в промышленную эксплуатацию, процесс изменения спроса на товары, обладающие способностью достигать неко­торого уровня насыщения, и др. Для моделирования таких процессов используются так называемые S-образные кривые роста, среди которых выделяют кривую Гомперца и логи­стическую кривую.

Кривая Гомперца имеет аналитическое выражение

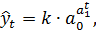(5.3)

где 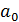, 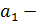положительные параметры, причем 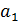меньше единицы; параметр k — асимптота функции.

В кривой Гомперца выделяются четыре участка: на пер­вом — прирост функции незначителен, на втором — при­рост увеличивается, на третьем участке прирост примерно постоянен, на четвертом — происходит замедление темпов прироста, и функция неограниченно приближается к значе­нию k. В результате конфигурация кривой напоминает латинскую букву S.

Логарифм данной функции является экспоненциальной кривой; логарифм отношения первого прироста к самой ор­динате функции — линейная функция времени.

На основании кривой Гомперца описывается, например, динамика показателей уровня жизни; модификации этой кривой используются в демографии для моделирования по­казателей смертности и т. д.

Логистическая кривая, или кривая Перла—Рида — воз­растающая функция, наиболее часто выражаемая в виде

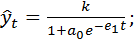(5. 4)

другие виды этой кривой:

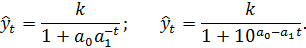
В этих выражениях 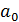и положительные параметры; предельное значение функции при бесконечном возрас­тании времени.

Если взять производную данной функции, то можно уви­деть, что скорость возрастания логистической кривой в ка­ждый момент времени пропорциональна достигнутому уров­ню функции и разности между предельным значением 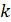и достигнутым уровнем. Логарифм отношения первого при­роста функции к квадрату ее значения (ординаты) есть ли­нейная функция от времени.

Конфигурация графика логистической кривой близка графику кривой Гомперца, но в отличие от последней логи­стическая кривая имеет точку симметрии, совпадающую с точкой перегиба.

Рассмотрим проблему предварительного выбора вида кривой роста для конкретного временного ряда. Допустим, имеется временной ряд .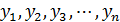

Для выбора вида полиномиальной кривой роста наи­более распространенным методом является метод конечных разностей (метод Тинтнера). Этот метод может быть ис­пользован для предварительного выбора полиномиальной кривой, если, во-первых, уровни временного ряда состоят только из двух компонент: тренд и случайная компонента, и во-вторых, тренд является достаточно гладким, чтобы его можно было аппроксимировать полиномом некоторой степени.

На первом этапе этого метода вычисляются разности (приросты) до 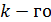порядка включительно:

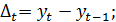
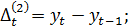
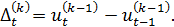
Для аппроксимации экономических процессов обычно вычисляют конечные разности до четвертого порядка.

Затем для исходного ряда и для каждого разностного ря­да вычисляются дисперсии по следующим формулам:

для исходного ряда

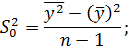
для разностного ряда 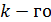порядка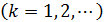

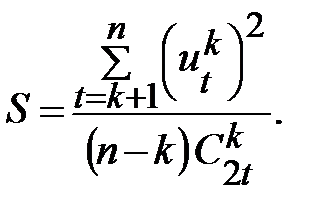
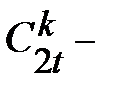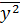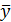В этих выражениях биномиальный коэффициент, и рассчитываются по формулам:

Производится сравнение отклонений каждой последую­щей дисперсии от предыдущей, т.е. вычисляются величины

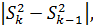
и если для какого-либо 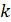эта величина не превосходит неко­торой наперед заданной положительной величины, т.е. дисперсии одного порядка, то степень аппроксимирующего полинома должна быть равна .

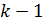Наиболее универсальным методом предварительного выбора кривых роста, позволяющим выбрать кривую из широкого класса кривых роста, является метод характеристик при­роста. Он основан на использовании отдельных характерных свойств кривых, рассмотренных выше. При этом методе исходный временной ряд предварительно сглаживается методом простой скользящей средней. Например, для ин­тервала сглаживания 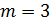сглаженные уровни рассчитыва­ются по формуле:

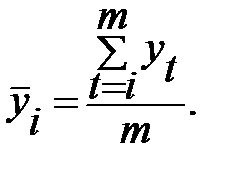
Причем чтобы не потерять первый и последний уровни, их сглаживают по формулам:

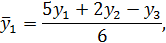
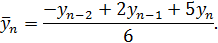
Затем вычисляются первые средние приросты

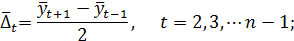
вторые средние приросты

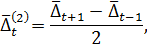
а также ряд производных величин, связанных с вычислен­ными средними приростами и сглаженными уровнями ряда:

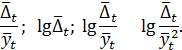
В соответствии с характером изменения средних при­ростов и производных показателей выбирается вид кривой роста для исходного временного ряда, при этом используется табл. 5.1.

Таблица 5.1

Показатель	Характеристика изменения показателя во времени	Вид кривой роста
Первый средний абсолютный прирост	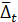Примерно одинаковы	Полином первого порядка (прямая)
Первый средний абсолютный прирост	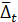Изменяются линейно	Полином второго порядка (парабола)
Второй средний прирост	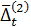Изменяются линейно	Полином третьего порядка (кубическая парабола)
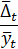	Примерно одинаковы	Простая экспонента
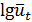	Изменяются линейно	Модифицированная экспонента
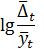	Изменяются линейно	Кривая Гамперца
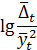	Изменяются линейно	Логическая кривая

На практике при предварительном выборе отбирают обыч­но две-три кривые роста для дальнейшего исследования и построения трендовой модели данного временного ряда.

Рассмотрим методы определения параметров отобранных кривых роста. Параметры полиномиальных кривых оцени­ваются, как правило, методом наименьших квадратов, суть которого заключается в том, чтобы сумма квадратов откло­нений фактических уровней ряда от соответствующих вы­равненных по кривой роста значений была наименьшей. Этот метод приводит к системе так называемых нормальных уравнений для определения неизвестных параметров отобран­ных кривых.

Для полинома первой степени

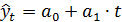
система нормальных уравнений имеет вид:

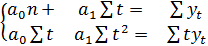(5.5)

где знак суммирования распространяется на все моменты наблюдения (все уровни) исходного временного ряда.

Аналогичная система для полинома второй степени

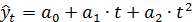
имеет вид:

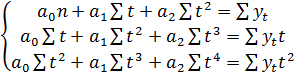(5.6)

Для полинома третьей степени

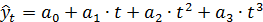
система нормальных уравнений записывается следующим образом:

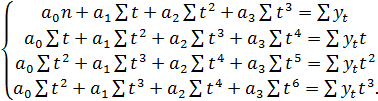(5.7)

Параметры экспоненциальных и S-образных кривых на­ходятся более сложными методами. Для простой экспоненты

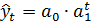
предварительно логарифмируют выражение по некоторому основанию (например, десятичному или натуральному):

,

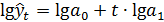т.е. для логарифма функции получают линейное выражение, а затем для неизвестных параметров 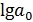и 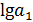составляют на основе метода наименьших квадратов систему нормальных уравнений, аналогичную системе для полинома первой степени. Решая эту систему, находят логарифмы параметров, а затем и сами параметры модели.

При определении параметров кривых роста, имеющих асимптоты (модифицированная экспонента, кривая Гомперца, логистическая кривая), различают два случая. Если значение асимптоты k известно заранее, то путем несложной моди­фикации формулы и последующего логарифмирования опре­деление параметров сводят к решению системы нормальных уравнений, неизвестными которой являются логарифмы параметров кривой.

Если значение асимптоты заранее неизвестно, то для нахождения параметров указанных выше кривых роста ис­пользуются приближенные методы: метод трех точек, метод трех сумм и др.

Таким образом, при моделировании экономической ди­намики, заданной временным рядом, путем сглаживания исходного ряда, определения наличия тренда, отбора одной или нескольких кривых роста и определения их параметров в случае наличия тренда получают одну или несколько трендовых моделей для исходного временного ряда. Встает во­прос, насколько эти модели близки к экономической реаль­ности, отраженной во временном ряду, насколько обосновано применение этих моделей для анализа и прогнозирования изучаемого экономического явления. Этот вопрос рассматри­вается в следующем параграфе.