По данным табл. 3.1: 1) оценить сменную среднюю добычу угля на одного рабочего для шахт с мощностью пласта 8 м;
2) найти 95%-ные доверительные интервалы для индивидуального и среднего значений сменной добычи угля на 1 рабочего для таких же шахт;
3) найти с надежностью 0,95 интервальные оценки коэффициента регрессии β1 и дисперсии σ2.
Решение. Уравнение регрессии Y по X (пример 3.1): 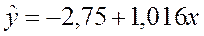 .
.
1. Оценим условное математическое ожидание Mx=8(Y).
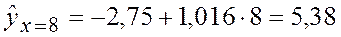 (т).
(т).
Составим таблицу (табл. 3.2) с учетом того, что 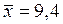 (м), а значения определяются по полученному уравнению регрессии.
(м), а значения определяются по полученному уравнению регрессии.
Таблица 3.2
| Xi | ∑ | ||||||||||
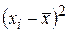 | 1,96 | 2,56 | 6,76 | 0,16 | 1,96 | 1,96 | 0,16 | 0,16 | 1,96 | 6,76 | 24,40 |
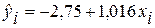 | 5.38 | 8.43 | 9,44 | 6,39 | 5.38 | 5,38 | 6,39 | 6,39 | 5,38 | 9,44 | − |
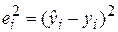 | 0.14 | 2,48 | 0,31 | 0,37 | 0,14 | 0,39 | 0,15 | 1,94 | 0,39 | 2,08 | 8,39 |
по (3.26): 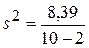 ,
,
по (3.33)
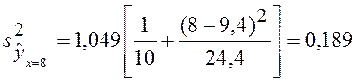
и 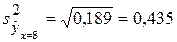 (т)
(т)
По табл. Стьюдента (приложений) 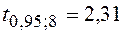 .
.
по (3.34) искомый доверительный интервал
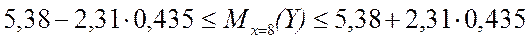 ,
,
или 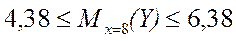 (т)
(т)
Итак, средняя сменная добыча угля на одного рабочего для шахт с мощностью пласта 8 м с надежностью 0,95 находится в пределах от 4,38 до 6,38 т.
2. доверительный интервал для индивидуального значения 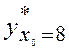 .
.
по (3.35):
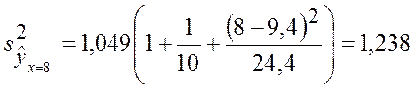
и 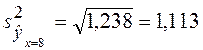 (т)
(т)
по (3.36):
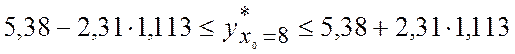
и 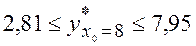
Таким образом, индивидуальная сменная добыча угля на одного рабочего для шахт с мощностью пласта 8 м с надежностью 0,95 находится в пределах от 2,81 до 7,95 т.
3. Найдем 95%-ный доверительный интервал для параметра. По (3.38)
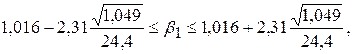
или 0,537 ≤ β 1 ≤ 1,495, т. е. с надежностью 0,95 при изменении мощности пласта X на 1 м суточная выработка Y будет изменяться на величину, заключенную в интервале от 0,537 до 1,495 (т).
Найдем 95%-ный доверительный интервал для параметра σ2.
Учитывая, что 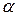 = 1−0,95=0,05, найдем по таблице III приложений
= 1−0,95=0,05, найдем по таблице III приложений
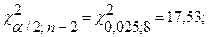
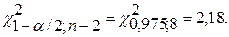
формуле (3.39)
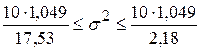
или 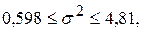 , и
, и 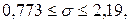 .
.
Таким образом, с надежностью 0,95 дисперсия возмущений заключена в пределах от 0,598 до 4,81, а их стандартное отклонение − от 0,773 до 2,19 (т).
Множественный регрессионный анализ
4.1. Классическая нормальная линейная модель множественной регрессии
модель множественной линейной регрессии:
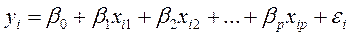 , (4.1)
, (4.1)
Введем обозначения: 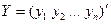 – матрица-столбец, или вектор, значений зависимой переменной.
– матрица-столбец, или вектор, значений зависимой переменной.
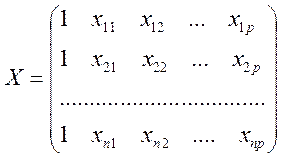
– матрица значений объясняющих переменных, или матрица плана размера
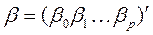 – матрица-столбец, или вектор, параметров размера
– матрица-столбец, или вектор, параметров размера 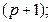
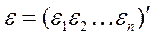 – матрица-столбец, или вектор, возмущений (случайных ошибок, остатков) размера
– матрица-столбец, или вектор, возмущений (случайных ошибок, остатков) размера 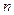 .
.
в матричной форме модель (4.1) примет вид:
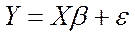 (4.2)
(4.2)
Оценкой этой модели по выборке является уравнение
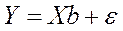 , (4.2)'
, (4.2)'
Где 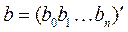 ,
, 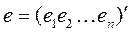 .
.
4.2. Оценка параметров классической регрессионной модели методом наименьших квадратов
Система нормальных уравнений в матричной форме для определения вектора 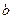 :
:
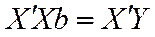 . (4.5)
. (4.5)
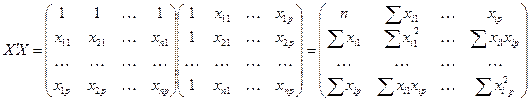 (4.6)
(4.6)
Матрица 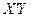 есть вектор произведений
есть вектор произведений 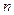 наблюдений объясняющих и зависимой переменных:
наблюдений объясняющих и зависимой переменных:
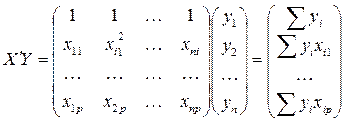 . (4.7)
. (4.7)
Решением уравнения (4.5) является вектор
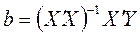 , (4.8)
, (4.8)
где 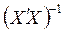 – матрица, обратная матрице коэффициентов системы (4.5),
– матрица, обратная матрице коэффициентов системы (4.5), 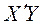 – матрица-столбец, или вектор, ее свободных членов.
– матрица-столбец, или вектор, ее свободных членов.
Зная вектор 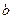 , выборочное уравнение множественной регрессии представим в виде:
, выборочное уравнение множественной регрессии представим в виде:
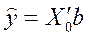 (4.9)
(4.9)
где 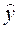 – групповая (условная) средняя переменной
– групповая (условная) средняя переменной 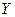 при заданном векторе значений объясняющей переменной
при заданном векторе значений объясняющей переменной
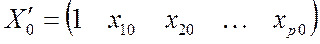 .
.
Пример 4.1. Имеются следующие данные (условные) о сменной добыче угля на одного рабочего 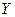 (т), мощности пласта
(т), мощности пласта 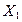 (м) и уровне механизации работ
(м) и уровне механизации работ 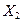 (%), характеризующие процесс добычи угля в 10 шахтах.
(%), характеризующие процесс добычи угля в 10 шахтах.
Таблица 4.1
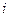 | 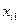 | 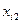 | 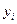 | 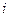 | 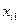 | 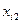 | 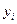 |
Предполагая, что между переменными 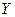 ,
, 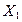 и
и 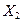 существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии
существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии 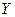 no
no 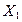 и
и 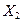 ).
).
Решение. Обозначим
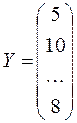 ,
, 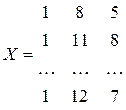
(в матрицу 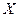 вводится дополнительный столбец чисел, состоящий из единиц).
вводится дополнительный столбец чисел, состоящий из единиц).
Таблица 4.2
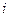 | 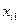 | 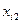 | 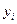 | 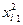 | 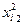 | 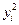 | 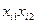 | 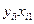 | 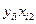 | 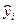 |  |
| 5,13 | 0,016 | ||||||||||
| 8,79 | 1,464 | ||||||||||
| 9,64 | 1,127 | ||||||||||
| 5,98 | 1,038 | ||||||||||
| 5,86 | 0,741 | ||||||||||
| 6,23 | 0,052 | ||||||||||
| 6,35 | 0,121 | ||||||||||
| 5,61 | 0,377 | ||||||||||
| 5,13 | 0,762 | ||||||||||
| 9,28 | 1,631 | ||||||||||
 | - | 6,329 |
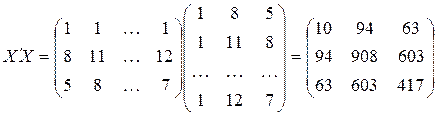
(см. суммы в итоговой строке табл. 4.2);
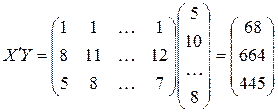
Матрицу 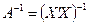 определим по формуле
определим по формуле 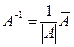 где
где 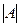 – определитель матрицы
– определитель матрицы 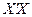 ;
; 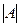 присоединенная к матрице
присоединенная к матрице 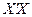 . Получим
. Получим
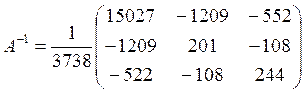
(самостоятельно).
Теперь в соответствии с (4.8) умножая эту матрицу на вектор
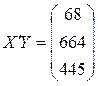 ,
,
получим 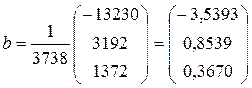 .
.
С учетом (4.9) уравнение множественной регрессии имеет вид: 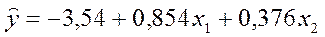 .
.
На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии 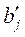 и коэффициенты эластичности
и коэффициенты эластичности 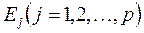 :
:
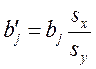 ; (4.10)
; (4.10)
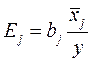 . (4.11)
. (4.11)
Стандартизованный коэффициент регрессии 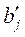 показывает, на сколько величин
показывает, на сколько величин 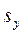 изменится в среднем зависимая
изменится в среднем зависимая 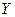 переменная при увеличении только
переменная при увеличении только 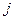 -й объясняющей переменной на
-й объясняющей переменной на 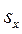 , а коэффициент эластичности
, а коэффициент эластичности 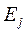 – на сколько процентов (от средней) изменится в среднем
– на сколько процентов (от средней) изменится в среднем 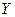 при увеличении только
при увеличении только 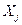 на 1%.
на 1%.
 2015-05-18
2015-05-18 3771
3771








