Рис. 3.1
Уравнение регрессии (3.2) будем искать в виде линейного уравнения
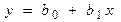 (3.3)
(3.3)
Отвлечемся на время от рассматриваемого примера и найдем формулы расчета неизвестных параметров уравнения линейной регрессии.
Согласно методу наименьших квадратов
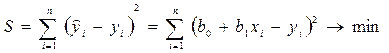 (3.4)
(3.4)
Система нормальных уравнений для определения параметров линейной регрессии:
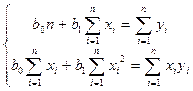 (3.5)
(3.5)
Разделив обе части уравнений (3.5) на п, получим систему нормальных уравнений в виде:
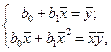 (3.6)
(3.6)
где 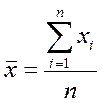 (3.7)
(3.7) 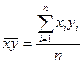 (3.9)
(3.9)
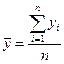 (3.8)
(3.8) 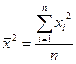 (3.10)
(3.10)
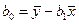 (3.11)
(3.11)
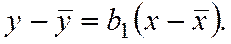
(3.12)
Коэффициент 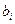 называется выборочным коэффициентом регрессии (или просто коэффициентом регрессии)
называется выборочным коэффициентом регрессии (или просто коэффициентом регрессии) 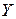 no
no 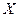 .
.
Коэффициент регрессии 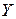 по
по 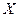 показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной на одну единицу.
показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной на одну единицу.
Решая систему (3.6),
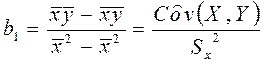 (3.13)
(3.13)
где 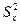 — выборочная дисперсия переменной X:
— выборочная дисперсия переменной X:
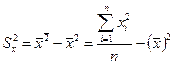 , (3.14)
, (3.14)
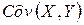 — выборочный корреляционный момент или выборочная
— выборочный корреляционный момент или выборочная
ковариация:
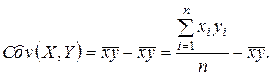
(3.15)
Пример 3.1. По данным табл. 3.1 найти уравнение регрессии 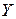 по
по 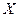 .
.
Решение. Вычислим все необходимые суммы:
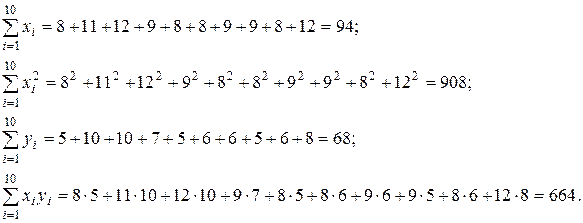
Затем по формулам (3.7) – (3.15) находим выборочны характеристики и параметры уравнений регрессии:
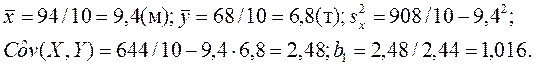
уравнение регрессии У по X:
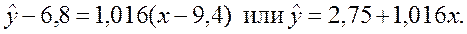
Из уравнения регрессии следует, что при увеличении мощности пласта X на 1 м добыча угля на одного рабочего Y увеличивается в среднем на 1,016 т (в усл. ед.).
Представим уравнение (3.12) в эквивалентном виде:
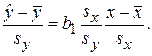
В этой системе величина
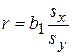 (3.17)
(3.17)
показывает, на сколько величин sy изменится в среднем Y, когда X увеличится на одно sx.
Величина r является показателем тесноты связи и называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции).
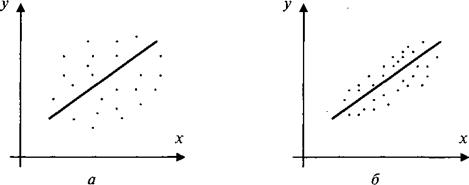
Рис. 3.2
Если r > 0 (b1 > 0), то корреляционная связь между переменными называется прямой, если, r < 0 (b1 < 0) − обратной.
Учитывая (3.13):
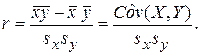 (3.18)
(3.18)
Или 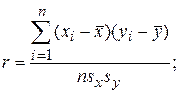 (3.19)
(3.19)
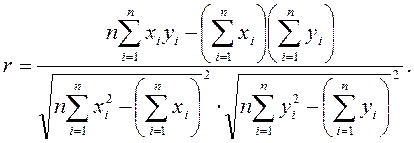 (3.20)
(3.20)
Для практических расчетов наиболее удобна формула (3.20).
Свойства.
1. Коэффициент корреляции принимает значения на отрезке [−1;1], т. е. −1 < r <1.Чем ближе │ r│ к единице, тем теснее связь.
2. При r = ±1 корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой линии.
3. При r = 0 линейная корреляционная связь отсутствует. При этом линия регрессии параллельна оси Ох
Пример 3.2.
По данным табл. 3.1 вычислить коэффициент корреляции между переменными X и Y.
Решение. 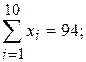 ;
;
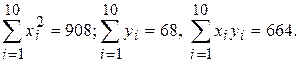
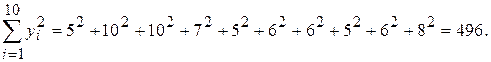
По формуле (3.20)
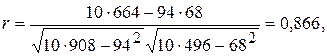
т.е.связь между переменными тесная.
3.4. Основные положения регрессионного анализа. Оценка параметров парной регрессионной модели. Теорема Гаусса−Маркова
Рассмотрим линейный регрессионный анализ, для которого функции 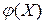 линейна относительно оцениваемых параметров:
линейна относительно оцениваемых параметров:
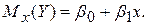 (3.21)
(3.21)
Предположим, что для оценки параметров линейной функции регрессии (3.21) взята выборка, содержащая n пар значений переменных (xi yi), где i =1,2,..., п. В этом случае линейная парная регрессионная модель имеет вид:
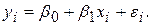 (3.22)
(3.22)
Основные предпосылки регрессионного анализа.
1. В модели (3.22) возмущение 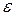 i (или зависимая переменная yi) есть величина случайная, а объясняющая переменная xi − величина неслучайная.
i (или зависимая переменная yi) есть величина случайная, а объясняющая переменная xi − величина неслучайная.
2. Математическое ожидание возмущения 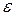 i равно нулю:
i равно нулю:
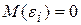 (3.23)
(3.23)
(или математическое ожидание зависимой переменной yi равно линейной функции регрессии: 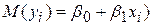 .
.
3. Дисперсия возмущения 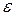 i (или зависимой переменной уi) постоянна для любого i:
i (или зависимой переменной уi) постоянна для любого i:
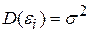 (3.24)
(3.24)
(или 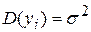 ) − условие гомоскедастичности или равноизменчивости возмущения (зависимой переменной)).
) − условие гомоскедастичности или равноизменчивости возмущения (зависимой переменной)).
4. Возмущения 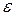 i и
i и 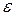 j (или переменные и yj) не коррелированы:
j (или переменные и yj) не коррелированы:
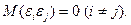 (3.25)
(3.25)
5. Возмущение 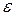 i (или зависимая переменная yi) есть нормально распределенная случайная величина.
i (или зависимая переменная yi) есть нормально распределенная случайная величина.
Воздействие неучтенных случайных факторов и ошибок наблюдений в модели (3.22) определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии 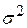 . Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия
. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия
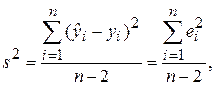 (3.26)
(3.26)
где 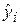 − групповая средняя, найденная по уравнению регрессии;
− групповая средняя, найденная по уравнению регрессии;
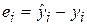 − выборочная оценка возмущения
− выборочная оценка возмущения 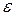 i или остаток регрессии.
i или остаток регрессии.
Теорема Гаусса−Маркова. Если регрессионная модель (3.22) удовлетворяет предпосылкам 1−4, то оценки b0 (3.11), b1 (3.13) имеют наименьшую дисперсию в классе всех линейных несмещенных оценок
Таким образом, оценки b0 и b1 в определенном смысле являются наиболее эффективными линейными оценками параметров β0 и β1
3.5. Интервальная оценка функции регрессии и ее параметров
Доверительный интервал для функции регрессии (условного математического ожидания).
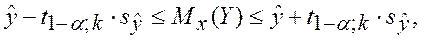 (3.34)
(3.34)
t −распределение Стьюдента с k = п − 2 степенями свободы
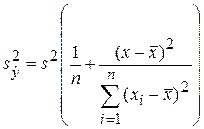 . (3.33)
. (3.33)
Доверительный интервал для индивидуальных значений зависимой переменной.
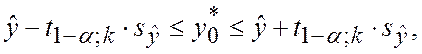
 (3.36)
(3.36)
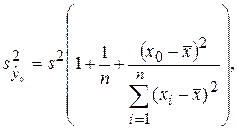 (3.35)
(3.35)
 2015-05-18
2015-05-18 1300
1300