2015-05-18
2994
 | нулевой средней величине | ||
| нормальном законе распределения | |||
| случайном характере | |||
| гомоскедастичности |
Решение
Оценка называется несмещенной, если математическое ожидание остатков равно нулю. Если оценка параметров регрессии является смещенной, то математическое ожидание остатков отличается от нуля, и при большом количестве выборочных оцениваний остатки будут накапливаться.
Нарушается предпосылка о нулевой средней величине остатков.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 60.
2. Несмещенность оценок параметров регрессии означает, что …
| | математическое ожидание остатков равно нулю | ||
| дисперсия остатков минимальная | |||
| точность оценок выборки увеличивается с увеличением объема выборки | |||
дисперсия остатков не зависит от величины  |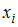
Решение
Несмещенность оценок параметров регрессии означает, что математическое ожидание остатков равно нулю.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 60.
3. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
| | |||
| -1 | |||
 |
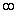Решение
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие несмещенности оценки формулируется следующим образом: «Оценка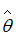 
параметра 
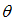называется несмещенной, если математическое ожидание 
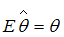»; где 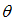– истинное значение параметра, вычисленное для генеральной совокупности. Математическое ожидание 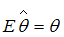в том случае, если 
.
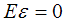Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 63.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 77–82.
4. Состоятельность оценок параметров регрессии означает, что …
| | точность оценок выборки увеличивается с увеличением объема выборки | ||
| математическое ожидание остатков равно нулю | |||
| дисперсия остатков минимальная | |||
| дисперсия остатков не зависит от величины |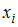
Решение
Состоятельность оценок параметров регрессии означает, что точность оценок выборки увеличивается с увеличением объема выборки.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 60.
5. Пусть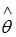 
– оценка параметра 
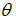регрессионной модели, полученная с помощью метода наименьших квадратов; 
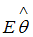– математическое ожидание оценки 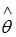. В том случае если 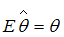, то оценка обладает свойством …
| | несмещенности | ||
| состоятельности | |||
| эффективности | |||
| смещенности |
Решение
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие несмещенности оценки формулируется следующим образом: «Оценка 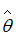параметра 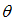называется несмещенной, если математическое ожидание 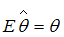»; где 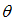– истинное значение параметра, вычисленное для генеральной совокупности. Поэтому правильный ответ – «несмещенности».
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 63.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 77–82.
