Оценки для математического ожидания и дисперсии

Пусть имеется случайная величина X, и ее параметры математическое ожидание а и дисперсия 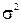неизвестны. Над величиной X произведеноn независимых опытов, давших результаты x_1,x_2, x_n.

Не уменьшая общности рассуждений, будем считать эти значения случайной величины различными. Будем рассматривать значения x_1,x_2, x_nкак независимые, одинаково распределенные случайные величины X_1,X_2, X_n.

Простейший метод статистического оценивания – метод подстановки и аналогии – состоит в том, что в качестве оценки той или иной числовой характеристики (среднего, дисперсии и др.) генеральной совокупности берут соответствующую характеристику распределения выборки – выборочную характеристику.

По методу подстановки в качестве оценки 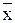математического ожидания а надо взять математическое ожидание распределения выборки – выборочное среднее. Таким образом, получаем

.

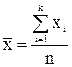
Чтобы проверить несмещенность и состоятельность выборочного среднего как оценки а, рассмотрим эту статистику как функцию выбранного вектора (X_1,X_2, X_n). Приняв во внимание, что каждая из величин X_1,X_2, X_n имеет тот же закон распределения, что и величина X, заключаем, что и числовые характеристики этих величин и величины X одинаковые: M(X _i) = M(X) = a, D(X _i) = D(X) = 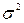, i = 1, 2, n, причем X_i – независимые в совокупности случайные величины.

Следовательно,

,

.

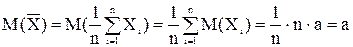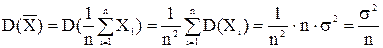Отсюда по определению получаем, что 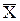– несмещенная оценка а, и так как D(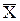)®0 при n®¥, то в силу теоремы предыдущего параграфа 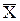является состоятельной оценкой математического ожидания а генеральной совокупности.

Эффективность или неэффективность оценки зависит от вида закона распределения случайной величины X. Можно доказать, что если величина X распределена по нормальному закону, то оценка 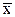является эффективной. Для других законов распределения это может быть не так.

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия

,

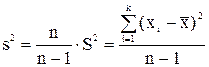так как 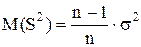, где 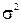– генеральная дисперсия. Действительно,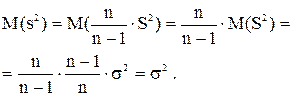

Оценка s_­­² для генеральной дисперсии является также и состоятельной, но не является эффективной. Однако в случае нормального распределения она является «асимптотически эффективной», то есть при увеличении n отношение ее дисперсии к минимально возможной неограниченно приближается к единице.

Итак, если дана выборка из распределения F(x) случайной величины X с неизвестным математическим ожиданием а и дисперсией 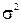, то для вычисления значений этих параметров мы имеем право пользоваться следующими приближенными формулами:

a ,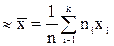

.

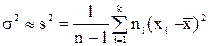Здесь x­_i­  – варианта выборки, n­_i ­– частота варианты x_{i, ­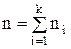} - объем выборки.
Для вычисления исправленной выборочной дисперсии более удобна формула

.

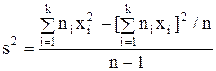Для упрощения расчета целесообразно перейти к условным вариантам 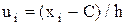(в качестве с выгодно брать первоначальную варианту, расположенную в середине интервального вариационного ряда). Тогда

, .

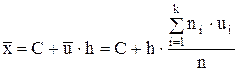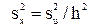Интервальное оценивание

Выше мы рассмотрели вопрос об оценке неизвестного параметра а одним числом. Такие оценки мы назвали точечными. Они имеют тот недостаток, что при малом объеме выборки могут значительно отличаться от оцениваемых параметров. Поэтому, чтобы получить представление о близости между параметром и его оценкой, в математической статистике вводятся, так называемые, интервальные оценки.

Пусть во выборке для параметра q найдена точечная оценка q^*. Обычно исследователи заранее задаются некоторой достаточно большой вероятностью g (например, 0,95; 0,99 или 0,999) такой, что событие с вероятностью g можно считать практически достоверным, и ставят вопрос об отыскании такого значения e > 0, для которого

.

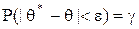Видоизменив это равенство, получим:

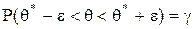
и будем в этом случае говорить, что интервал ]q^*- e; q^*+ e[ покрывает оцениваемый параметр q с вероятностью g.

Интервал ]q^*-e; q^*+e [ называется доверительным интервалом.

Вероятность g называется надежностью (доверительной вероятностью) интервальной оценки.

Концы доверительного интервала, т.е. точки q^*-e и q^*+e называются доверительными границами.

Число e называется точностью оценки.

В качестве примера задачи об определении доверительных границ, рассмотрим вопрос об оценке математического ожидания случайной величины Х, имеющей нормальный закон распределения с параметрами а и s, т.е. Х = N(a, s). Математическое ожидание в этом случае равно а. По наблюдениям Х₁, Х₂, Х_n вычислим среднее 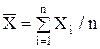и оценку 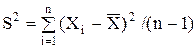дисперсии s².

Оказывается, что по данным выборки можно построить случайную величину

,

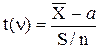которая имеет распределение Стьюдента (или t-распределение) с n = n –1 степенями свободы.

Воспользуемся таблицей П.1.3 и найдем для заданных вероятности g и числа n число t_g такое, при котором вероятность

P(|t(n)| < t_g) = g,

или

.

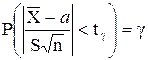Сделав очевидные преобразования получим,

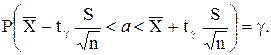
Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал

,

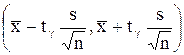покрывающий неизвестный параметр а с надежностью g. Здесь случайные величины 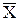и S заменены неслучайными величинами 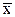и s, найденными по выборке. По таблице П.1.3, по заданным n и g можно найти t_g.

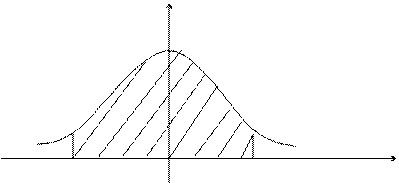
Графическая иллюстрация схемы нахождения точности e и доверительных границ, отвечающих надежности g приведена на рис. 14.1.

j(t)

 

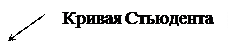-t_g 0 t_g t

 

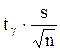
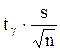
0 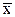x

Рис. 14.1

Замечание. При n® ¥ распределение Стьюдента стремится к нормальному распределению. Поэтому при больших n (практически при n > 120) t_g можно получить по таблице П.1.2 из уравнения Ф(t_g) = g/2.

Для оценки среднего квадратического отклонения s нормально распределенного количественного признака Х с надежностью g по исправленному выборочному среднему квадратическому отклонению s служат доверительные интервалы:

s(1-q) < s < s(1 + q) при q < 1,

0 < s < s(1 + q) при q > 1,

где q находят по таблице П.1.4 по заданным n и g.

Задача 14.1. Найти доверительные интервалы для оценки математического ожидания а и среднего квадратического отклонения s диаметра деревьев сосны по результатам вычислений из §13.4. Надежность g = 0,95.

Решение. В §13.4 были получены следующие точечные оценки а» =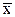
= 30,77см, 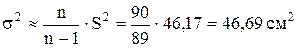, где n = 90 – объем выборки. Следовательно, s» s = 6,83см.

По таблице П.1.3 при g =0,95 и n = 90 находим t_g= 1,987. Вычисляем точность оценки 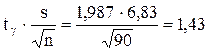, доверительные границы 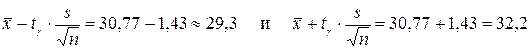. Получаем доверительный интервал 29,3< a < 32,2.

Находим доверительный интервал для оценки s. По таблице П.1.4 при g =
= 0,95 и n = 90 получаем q = 0,151. Вычисляем доверительные границы
s(1 – q) = 6,83 × 0,849» 5,8 и s(1 + q) = 6,83 × 1,151» 7,9. Получаем доверительный интервал 5,8<s<7,9.

Оценки истинного значения измеряемой величины и точности
измерений

Пусть производится n измерений некоторой физической константы, истинное значение которой а неизвестно. Измерения будем рассматривать прямые, независимые, равноточные и не дающие систематической ошибки.

Измерения называются:

- прямыми, если результаты измерений считываются непосредственно со шкалы измерительного прибора;

- независимыми, если результат каждого измерения не может повлиять на результаты остальных измерений;

- равноточными, если измерения проводятся в одинаковых условиях.

Результаты измерений не будут содержать систематической ошибки, если применяется исправный измерительный прибор.

В этих условиях результаты измерений х₁, х₂, х_n можно считать случайными величинами, которые независимы, имеют один и тот же закон распределения – нормальный с параметрами (а, s), где а – истинное значение измеряемой величины (математическое ожидание), s – точность измерительного прибора (средне квадратическое отклонение).

Следовательно, мы можем оценивать с помощью доверительных интервалов истинное значение а измеряемой величины по выборочной средней 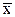, а точность измерений s по выборочному стандарту s, применяя изложенные выше методы.

Проверка статистических гипотез

Основные сведения

Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

Нулевой (основной) называют выдвинутую гипотезу Н₀.

Конкурирующий (альтернативной) называют гипотезу Н₁, которая противоречит нулевой гипотезе. В итоге проверки гипотезы могут быть совершены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки первого рода называют уровнем значимости и обозначают через a. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости равный 0,05, то это означает, что в среднем в пяти случаях из ста мы рискуем допустить ошибку первого рода (отвергнуть правильную гипотезу).

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность ошибки второго рода обозначают через b. Величина 1–b называется мощностью критерия.

Статистическим критерием (или просто критерием) называют случайную величину К, которая служит для проверки гипотезы. Его значения позволяют судить о «расхождении выборки с гипотезой». Критерий, будучи величиной случайной в силу случайности выборки Х₁, Х₂, Х_n, подчиняется при выполнении гипотезы Н₀ некоторому известному, затабулированному закону распределения.

Для проверки гипотезы по данным выборки вычисляют частные значения входящих в критерий величин, и таким образом получают частное (наблюдаемое) значение критерия.

Наблюдаемым (эмпирическим) значением К_набл. называют то значение критерия, которое вычислено по выборкам.

После выбора определенного критерия, множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другое – при которых она принимается.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.

Критическими точками (границами) k_кр называют точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую неравенством K > k_кр, где k_кр – положительное число.

Левосторонней называют критическую область, определяемую неравенством К < k_кр, где k_кр – отрицательное число.

Двусторонней называют критическую область, определяемую неравенствами К < k₁, К > k₂, где k₂ > k₁ .

В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами (в предположении, что k_кр > 0):

К < –k_кр , К > k_кр ,

или равносильным неравенством |K| > k_кр.

Для отыскания, например, правосторонней критической области поступают следующим образом. Сначала задаются достаточно малой вероятностью – уровнем значимости a. Затем ищут критическую точку k_кр, исходя из требования, чтобы при условии справедливости нулевой гипотезы, вероятность того, что критерий К примет значение, больше k_кр., была равна принятому уровню значимости:

Р(К> k_кр) = a.

Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию. Когда критическая точка уже найдена, вычисляют по данным выборок наблюдаемое значение критерия и, если окажется, что К_набл > k_кр, то нулевую гипотезу отвергают; если же К_набл < k_кр, то нет оснований, чтобы отвергнуть нулевую гипотезу. Но это вовсе не означает, что Н₀ является единствено подходящей гипотезой: просто расхождение между выборочными данными и гипотезой Н₀ невелико, или иначе Н₀ не противоречит результатам наблюдений; однако таким же свойством наряду с Н₀ могут обладать и другие гипотезы.

Методы, которые для каждой выборки формально точно определяют, удовлетворяют выборочные данные нулевой гипотезе или нет, называются критериями значимости.

Критерии значимости подразделяются на три типа:

1. Критерии значимости, которые служат для проверки гипотез о параметрах распределений генеральной совокупности (чаще всего нормального распределения). Эти критерии называются параметрическими.

2. Критерии, которые для проверки гипотез не используют предположений о распределении генеральной совокупности. Эти критерии не требуют знаний параметров распределения, поэтому называются непараметрическими.

3. Особую группу критериев составляют критерии согласия, служащие для проверки гипотез о согласии распределения генеральной совокупности, из которой получена выборка, с ранее принятой теоретической моделью (чаще всего нормальным распределением).

Сравнение двух дисперсий нормальных генеральных совокупностей

На практике задача сравнения дисперсий возникает, если требуется сравнить точность приборов, инструментов, самих методов измерений и т.д. Очевидно, предпочтительнее тот прибор, инструмент и метод, который обеспечивает наименьшее рассеяние результатов измерений, т.е. наименьшую дисперсию.

Пусть необходимо проверить гипотезу о том, что две независимые выборки получены из генеральных совокупностей Х и Y с одинаковыми дисперсиями s_х² и s_y². Для этого используется F–критерий Фишера.

Порядок применения F–критерия следующий:

1. Принимается предположение о нормальности распределения генеральных совокупностей. При заданном уровне значимости a формулируется нулевая гипотеза Н₀: s_х² = s_y² о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе Н₁: s_х² > s_y².

2. Получают две независимые выборки из совокупностей Х и Y объемом n_x и n_y соответственно.

3. Рассчитывают значения исправленных выборочных дисперсий s_х² и s_y² (методы расчета рассмотрены в §13.4). Большую из дисперсий (s_х² или s_y²) обозначают s₁², меньшую – s₂².

4. Вычисляется значение F–критерия по формуле F_набл = s₁²/ s₂².

5. По таблице критических точек распределения Фишера – Снедекора, по заданному уровню значимости a и числом степеней свободы n₁ = n₁ - 1, n₂ = n₂ - 1 (n₁ – число степеней свободы большей исправленной дисперсии), находится критическая точка F_кр(a, n₁, n₂).

Отметим, что в таблице П.1.7 приведены критические значения одностороннего F–критерия. Поэтому, если применяется двусторонний критерий (Н₁: s_х² ¹ s_y²), то правостороннюю критическую точку F_кр(a/2, n₁, n₂) ищут по уровню значимости a/2 (вдвое меньше заданного) и числам степеней свободы n₁ и n₂ (n₁ – число степеней свободы большей дисперсии). Левостороннюю критическую точку можно и не отыскивать.

6. Делается вывод: если вычисленное значение F–критерия больше или равно критическому (F_набл ³ F_кр), то дисперсии различаются значимо на заданном уровне значимости. В противном случае (F_набл < F_кр) нет оснований для отклонения нулевой гипотезы о равенстве двух дисперсий.

Задача 15.1. Расход сырья на единицу продукции по старой технологии составил:

Расход сырья хi
Число изделий mi				nx = 9

По новой технологии:

Расход сырья yi
Число изделий ni					ny = 13

Предположив, что соответствующие генеральные совокупности X и Y имеют нормальные распределения, проверить, что по вариативности расход сырья по новой и старой технологиям не отличаются, если принять уровень значимости a = 0,1.

Решение. Действуем в порядке, указанном выше.

1. Будем судить о вариативности расхода сырья по новой и старой технологиям по величинам дисперсий. Таким образом, нулевая гипотеза имеет вид Н₀: s_х² = s_y². В качестве конкурирующей примем гипотезу Н₁: s_х² ¹ s_y², поскольку заранее не уверены в том, что какая–либо из генеральных дисперсий больше другой.

2–3. Найдем выборочные дисперсии. Для упрощения вычислений перейдем к условным вариантам:

u_i = x_i - 307, v_i = y_i - 304.

Все вычисления оформим в виде следующих таблиц:

ui	mi	miui	miui2	mi(ui+1)2		vi	ni	nivi	nivi2	ni(vi+1)2
-3		-3				-1		-2
å	-
						å	-

Контроль: å m_iu_i² + 2å m_iu_i + m_i = Контроль: å n_iv_i² + 2å n_iv_i + n_i = 13 + 2 + 9 = 24 = 34 + 20 + 13 = 67

Найдем исправленные выборочные дисперсии:

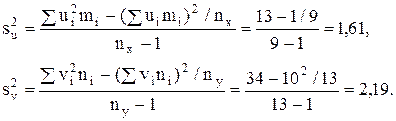
4. Сравним дисперсии. Найдем отношение большей исправленной дисперсии к меньшей:

.

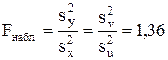5. По условию конкурирующая гипотеза имеет вид s_х² ¹ s_y², поэтому критическая область двусторонняя и при отыскании критической точки следует брать уровни значимости, вдвое меньше заданного.

По таблице П.1.7 по уровню значимости a/2 = 0,1/2 = 0,05 и числам степеней свободы n₁ = n₁ - 1 = 12, n₂ = n₂ - 1 = 8 находим критическую точку F_кр(0,05; 12; 8) = 3,28.

6. Так как F_набл. < F_кр то гипотезу о равенстве дисперсий расхода сырья при старой и новой технологиях принимаем.

Выше при проверке гипотез предполагалось нормальность распределения исследуемых случайных величин. Однако специальные исследования показали, что предложенные алгоритмы весьма устойчивы (особенно при больших объемах выборок) по отношению к отклонению от нормального распределения.