Регрессионный анализ предназначен для исследования зависимости исследуемой переменной от различных факторов и отображения их взаимосвязи в форме регрессионной модели. В регрессионных моделях зависимая (объясняемая) переменная Y может быть представлена в виде функции f (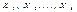 ), где
), где 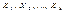 - независимые (объясняющие) переменные, или факторы.
- независимые (объясняющие) переменные, или факторы.
Связь между переменной Y иk независимыми факторами Х можно охарактеризовать функцией регрессии Y= f (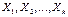 ), которая показывает, каково будет в среднем значение переменной yi, если переменные Xi примут конкретные значения. Данное обстоятельство позволяет использовать модель регрессии не только для анализа, но и для прогнозирования экономических явлений. Сформулируем регрессионную задачу для случая одного факторного признака.
), которая показывает, каково будет в среднем значение переменной yi, если переменные Xi примут конкретные значения. Данное обстоятельство позволяет использовать модель регрессии не только для анализа, но и для прогнозирования экономических явлений. Сформулируем регрессионную задачу для случая одного факторного признака.
Пусть имеется набор значений двух переменных: Y= 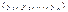 - объясняемая переменная и X=
- объясняемая переменная и X= 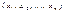 - объясняющая переменная, каждая из которых содержит n наблюдений. Пусть между переменными X=
- объясняющая переменная, каждая из которых содержит n наблюдений. Пусть между переменными X= 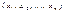 и Y=
и Y= 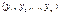 теоретически существует некоторая линейная зависимость
теоретически существует некоторая линейная зависимость 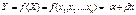 Данное уравнение будем называть «истинным» уравнением регрессии. Однако в действительности между X и Y наблюдается не столь жесткая связь. Отдельные наблюдения
Данное уравнение будем называть «истинным» уравнением регрессии. Однако в действительности между X и Y наблюдается не столь жесткая связь. Отдельные наблюдения 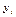 будут отклоняться от линейной зависимости в силу воздействия различных причин. Обычно зависимая переменная находится под влиянием целого ряда факторов, в том числе и не известных исследователю, а также случайных причин (возмущения и помехи); существенным источником отклонений в ряде случаев являются ошибки измерения. Отклонения от предполагаемой формы связи, естественно, могут возникнуть и в силу неправильного выбора вида самого уравнения, описывающего эту зависимость. Учитывая возможные отклонения, линейное уравнение связи двух переменных (парную регрессию) представим в виде
будут отклоняться от линейной зависимости в силу воздействия различных причин. Обычно зависимая переменная находится под влиянием целого ряда факторов, в том числе и не известных исследователю, а также случайных причин (возмущения и помехи); существенным источником отклонений в ряде случаев являются ошибки измерения. Отклонения от предполагаемой формы связи, естественно, могут возникнуть и в силу неправильного выбора вида самого уравнения, описывающего эту зависимость. Учитывая возможные отклонения, линейное уравнение связи двух переменных (парную регрессию) представим в виде 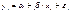 , (2) где
, (2) где 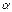 - постоянная величина (или свободный член уравнения),
- постоянная величина (или свободный член уравнения), 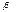 - коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений. Это показатель, характеризующий изменение переменной
- коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений. Это показатель, характеризующий изменение переменной 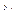 , при изменении значения
, при изменении значения 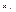 на единицу. Если
на единицу. Если 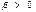 - переменные
- переменные 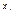 и
и 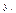 положительно коррелированные, если
положительно коррелированные, если 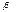 < 0 – отрицательно коррелированны;
< 0 – отрицательно коррелированны; 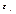 - случайная переменная, или случайная составляющая, или остаток, или возмущение. Она отражает тот факт, что изменение
- случайная переменная, или случайная составляющая, или остаток, или возмущение. Она отражает тот факт, что изменение 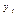 будет неточно описываться изменением Х – присутствуют другие факторы, неучтенные в данной модели.
будет неточно описываться изменением Х – присутствуют другие факторы, неучтенные в данной модели.
Таким образом, в уравнении (2) значение каждого наблюдения 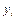 представлено как сумма двух частей — систематической
представлено как сумма двух частей — систематической 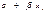 и случайной
и случайной 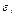 . В свою очередь систематическую часть можно представить в виде уравнения
. В свою очередь систематическую часть можно представить в виде уравнения 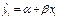 Можно сказать, что общим моментом для любой эконометрической модели является разбиение зависимой переменной на две части — объясненную и случайную.
Можно сказать, что общим моментом для любой эконометрической модели является разбиение зависимой переменной на две части — объясненную и случайную. 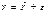 .
.
 2015-05-18
2015-05-18 4211
4211
