2015-05-18
230
По условию имеем
| x | y |
Все вычисления произведем в MS Excel
| ВЫВОД ИТОГОВ | |
| Регрессионная статистика | |
| Множественный R | 0,273633187 |
| R-квадрат | 0,074875121 |
| Нормированный R-квадрат | -0,027916532 |
| Стандартная ошибка | 4,54030823 |
| Наблюдения | |
| Дисперсионный анализ | |
| df | |
| Регрессия | |
| Остаток | |
| Итого | |
| Коэффициенты | |
| Y-пересечение | 103,4879227 |
| Переменная X 1 | 0,315821256 |
| SS | MS |
| 15,01586517 | 15,01586517 |
| 185,5295894 | 20,61439882 |
| 200,5454545 | |
| Стандартная ошибка | t-статистика |
| 1,91955706 | 53,91239723 |
| 0,370042421 | 0,853473111 |
| F | Значимость F | |||
| 0,728416351 | 0,415533692 | |||
| P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| 1,30671E-12 | 99,14558296 | 107,8302624 | 99,14558296 | 107,8302624 |
| 0,415533692 | -0,521272855 | 1,152915367 | -0,521272855 | 1,152915367 |
Итак,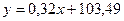 
- уравнение линейной регрессии.
|
|
|
Поскольку коэффициент парной линейной корреляции равен 0,27, то связь между х и у, скорее всего, не является линейной.
Статистика критерия Фишера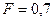 
, 
, 
.
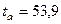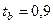Так как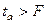 
, 
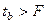, то коэффициенты линейной корреляции статистически не значимы, т.е. уравнение линейной регрессии нельзя применять для прогноза.
