Отличное от нуля значение спина ядра J является причиной возникновения сверхтонкой структуры оптических спектров.
Как известно, электрон обладает полным механическим моментом количества движения 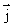 , который складывается из его собственного механического момента
, который складывается из его собственного механического момента 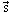 =
= 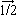 и орбитального момента
и орбитального момента 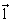
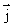 =
= 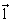 +
+ 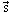 =
= 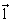 +
+ 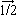 .
.
Механический момент атома 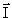 , обусловленный электронной оболочкой атома, складывается из механических моментов количества движения его электронов
, обусловленный электронной оболочкой атома, складывается из механических моментов количества движения его электронов
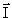 =
= 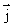 1 +
1 + 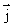 2 +... +
2 +... + 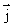 n,
n,
где n – число электронов в атоме.
Электроны внутренних заполненных оболочек атома имеют суммарный момент 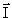 внутр= 0. Поэтому механический момент электронной оболочки атома определяется электронами внешних оболочек. Механическому моменту атома
внутр= 0. Поэтому механический момент электронной оболочки атома определяется электронами внешних оболочек. Механическому моменту атома 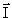 , который называют спином электронной оболочки атома, соответствует магнитный момент
, который называют спином электронной оболочки атома, соответствует магнитный момент
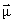 атома = g
атома = g 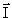 .
.
Величина g называется гиромагнитным отношением. Вектора 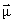 атома и
атома и 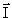 коллинеарны.
коллинеарны.
Среднее магнитное поле 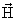 e, создаваемое внешними электронами в центре атома, там, где расположено атомное ядро, зависит от спин электронной оболочки
e, создаваемое внешними электронами в центре атома, там, где расположено атомное ядро, зависит от спин электронной оболочки 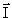 :
:
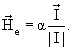
Магнитный момент ядра 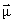 ядра также можно выразить через значение его спина
ядра также можно выразить через значение его спина 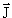 :
:
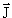 =
= 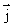 1 +
1 + 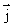 2 +... +
2 +... + 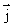 n =
n = 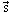 1 +
1 + 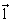 1 +
1 + 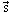 2 +
2 + 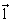 2 =... +
2 =... + 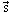 n +
n + 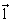 n,
n,
где 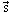 i – собственный механический момент нуклона,
i – собственный механический момент нуклона, 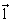 i – орбитальный механический момент нуклона,
i – орбитальный механический момент нуклона, 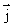 i – полный механический момент нуклона.
i – полный механический момент нуклона.
Магнитный момент ядра связан с его механическим моментом следующим соотношением:
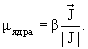
Энергия взаимодействия E магнитного момента ядра 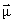 ядра с магнитным полем внешних электронов атома
ядра с магнитным полем внешних электронов атома 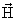 e определяется соотношением
e определяется соотношением
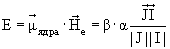
и зависит от взаимной ориентации спинов ядра 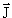 и внешней электронной оболочки
и внешней электронной оболочки 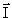 .
.
При учёте спина атомного ядра I полный механический момент количества движения атома (спин атома) 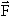 складывается из механического момента (спина) электронной оболочки
складывается из механического момента (спина) электронной оболочки 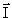 и полного механического момента (спина) ядра
и полного механического момента (спина) ядра 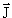 :
:
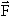 =
= 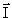 +
+ 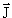 .
.
Согласно законам квантовой механики квадрат момента любой изолированной системы может принимать только целые или полуцелые значения:
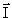 2 = ћ 2I(I+1),
2 = ћ 2I(I+1),
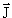 2 = ћ 2J(J+1),
2 = ћ 2J(J+1),
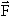 2 = ћ 2F(F+1).
2 = ћ 2F(F+1).
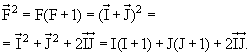
Энергия взаимодействия E магнитного момента ядра 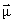 ядра с магнитным полем
ядра с магнитным полем 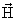 e электронной оболочки будет принимать дискретные значения, определяемые суммарным моментом
e электронной оболочки будет принимать дискретные значения, определяемые суммарным моментом 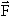 :
:
(I+J), (I+J−1), … |I−J|.
Каждому возможному значению 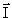
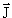 будет соответствовать отдельный уровень.
будет соответствовать отдельный уровень.
Если величина спина ядра 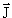 меньше величины спина электронной оболочки атома
меньше величины спина электронной оболочки атома 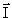 , то величина спина ядра может быть определена по числу линий сверхтонкого расщепления оптического спектра атома. Для возбуждения уровней сверхтонкой структуры атомных спектров используется лазерное излучение.
, то величина спина ядра может быть определена по числу линий сверхтонкого расщепления оптического спектра атома. Для возбуждения уровней сверхтонкой структуры атомных спектров используется лазерное излучение.
На Рис. 3 приведён спектр сверхтонкого расщепления уровней I = 9/2 и 11/2 атома 59Co. Из того, что число линий сверхтонкого расщепления N = 8 следует, что спин ядра J(59Co) = 7/2.
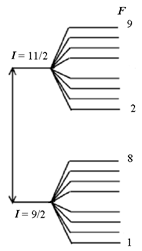
Рис. 3. Сверхтонкое расщепление уровней (изображены без соблюдения масштаба). Слева - нерасщепленные уровни, справа – расщепленные уровни атома 59Co.
 2015-05-18
2015-05-18 747
747








