Метод отклонений от тренда предполагает построение регрессионной модели отклонений (наблюдаемых значений от трендовых) исследуемых факторов. Для парной регрессии, например, проводят аналитическое выравнивание временных рядов изучаемых показателей, рассчитывая параметры модели 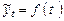 и и 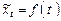 по временным данным. Затем проводят расчет отклонений от трендов: по временным данным. Затем проводят расчет отклонений от трендов: 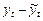 и и 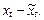 Для дальнейшего анализа используют не исходные данные, а отклонения от трендов, при условии, что последние не содержат тренда. Для дальнейшего анализа используют не исходные данные, а отклонения от трендов, при условии, что последние не содержат тренда.
|
Анализ на автокорреляцию остатков регрессионной модели зависимости факторов X и Y от времени. Проанализируем остатки временного ряда фактора Х, полученного на листе «Предварительный анализ рядов», на наличие автокорреляции (таблица 31).
Для проверки гипотезы о наличии автокорреляции остатков используется кроме статистики Дарбина–Уотсона (см. тему 1) на больших выборках выборочный коэффициент автокорреляции остатков первого порядка 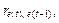 так как DW так как DW 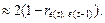
|
Таблица 31 – Анализ модели Х(t) на наличие автокорреляции остатков
|
|
|
| Коэффициент корреляции остатков | 0,75 |
| tнабл | 5,01 |
| tкр | 2,09 |
Так как коэффициент автокорреляции первого порядка значим (tнабл > tкр), то автокорреляция присутствует.
Для фактора Y автокорреляция отсутствует (таблица 32).
Таблица 32 – Анализ модели Y(t) на наличие автокорреляции остатков
| Коэффициент корреляции остатков | 0,42 |
| tнабл | 2,09 |
| tкр | 2,09 |
Устранение автокорреляции остатков во временном ряде X(t). Поскольку во временном ряде фактора Х присутствует автокорреляция, то модель этого ряда нельзя использовать в дальнейших исследованиях. Устраним автокорреляцию.
Для устранения автокорреляции можно воспользоваться обобщенным методом наименьших квадратов. Для применения ОМНК необходимо специфицировать модель автокорреляции регрессионных остатков. Обычно в качестве такой модели используется авторегрессионный процесс первого порядка AR(1). Для простоты изложения ограничимся случаем парной регрессии.
Пусть исходное уравнение регрессии 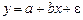 содержит автокорреляцию случайных членов.
Допустим, что автокорреляция подчиняется авторегрес- сионной схеме первого порядка содержит автокорреляцию случайных членов.
Допустим, что автокорреляция подчиняется авторегрес- сионной схеме первого порядка 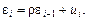 где r – коэффициент авторегрессии; иi – случайный член, удовлетворяющий предпосылкам МНК.
Данная схема является авторегрессионной, так как e определяется значениями этой же величины с запаздыванием, и схемой первого порядка, так как в этом случае запаздывание равно единице.
Величина r есть коэффициент корреляции между двумя соседними ошибками. Пусть r известно.
Обозначим где r – коэффициент авторегрессии; иi – случайный член, удовлетворяющий предпосылкам МНК.
Данная схема является авторегрессионной, так как e определяется значениями этой же величины с запаздыванием, и схемой первого порядка, так как в этом случае запаздывание равно единице.
Величина r есть коэффициент корреляции между двумя соседними ошибками. Пусть r известно.
Обозначим 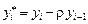 , , 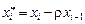 , , 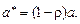 Это преобразование и называется авторегрессионым преобразованием первого порядка AR (1), или преобразованием Бокса–Дженкинса.
Тогда преобразованное уравнение принимает вид
Это преобразование и называется авторегрессионым преобразованием первого порядка AR (1), или преобразованием Бокса–Дженкинса.
Тогда преобразованное уравнение принимает вид
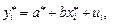 где i ³ 2. Это уравнение не содержит автокорреляцию и для оценки его параметров используется обычный МНК.
На практике величина r неизвестна. Наиболее простой способ оценить r – применить обычный МНК к регрессионному уравнению
где i ³ 2. Это уравнение не содержит автокорреляцию и для оценки его параметров используется обычный МНК.
На практике величина r неизвестна. Наиболее простой способ оценить r – применить обычный МНК к регрессионному уравнению 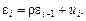 Коэффициент r можно также приближенно оценить, используя статистику Дарбина–Уот- сона: Коэффициент r можно также приближенно оценить, используя статистику Дарбина–Уот- сона: 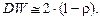
|
На листе «Устранение автокорреляции по Х» получена модель 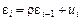 (таблица 33), в которой свободный член не значим (см. тему 1). Поэтому модель была уточнена (таблица 34).
(таблица 33), в которой свободный член не значим (см. тему 1). Поэтому модель была уточнена (таблица 34).
|
|
|
Таблица 33 – Результаты расчета параметров модели случайной
составляющей ряда фактора Х
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | –0,03 | 0,04 | –0,56 | 0,58 |
| Остатки по Х | 0,75 | 0,15 | 4,88 | 0,000 1 |
Таблица 34 – Результаты расчета параметров уточненной модели случайной
составляющей ряда фактора Х
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | #Н/Д | #Н/Д | #Н/Д | |
| Остатки по Х | 0,74 | 0,15 | 4,94 | 7,8E–05 |
Из таблицы 34 находим значение параметра r = 0,74. Используя авторегрессионное преобразование первого порядка AR(1), пересчитаны значения независимой переменной t * и зависимой переменной X* (таблица 35) и по данным значениям построена модель Х*= 2,17 + 0,19 t * (таблица 36), в которой отсутствует автокорреляция остатков (таблица 37). В дальнейшем будем использовать ее при построении модели методом отклонения от трендов.
Таблица 35 – Преобразованные значения переменных Х* и t *
| X* | t * |
| 2,38 | 1,26 |
| 2,31 | 1,52 |
| 2,53 | 1,77 |
| 2,34 | 2,03 |
| 2,5 | 2,29 |
| 2,59 | 2,55 |
| 2,68 | 2,80 |
| 3,04 | 3,06 |
| 3,03 | 3,32 |
| 3,10 | 3,58 |
| 3,12 | 3,83 |
| 3,04 | 4,09 |
| 2,97 | 4,35 |
| 3,2 | 4,61 |
| 3,19 | 4,87 |
| 3,21 | 5,12 |
Окончание таблицы 35
| X* | t * |
| 3,60 | 5,38 |
| 2,76 | 5,64 |
| 3,14 | 5,9 |
| 3,24 | 6,15 |
| 3,43 | 6,41 |
Таблица 36 – Результаты расчета параметров модели Х*(t *)
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | 2,18 | 0,12 | 18,27 | 1,64E–13 |
| t* | 0,19 | 0,03 | 6,77 | 1,84E–06 |
Таблица 37 – Анализ модели Х*(t *) на наличие автокорреляции остатков
| Коэффициент корреляции остатков | 0,17 |
| tнабл | 0,75 |
| tкр | 2,09 |
Построение регрессионной модели по отклонениям от трендов. Исходные данные (таблица 38) для построения модели по отклонениям и ее параметры (таблица 39) представлены на листе «Модель по отклонениям».
Таблица 38 – Отклонения факторов
| Месяц | Остатки модели X*(t*) | Остатки модели Y(t) |
| –0,04 | 0,18 | |
| –0,16 | –0,13 | |
| 0,01 | 0,001 | |
| –0,23 | –0,16 | |
| –0,13 | –0,34 | |
| –0,09 | –0,18 | |
| –0,04 | –0,10 | |
| 0,27 | 0,01 | |
| 0,21 | 0,22 | |
| 0,23 | 0,34 |
Окончание таблицы 38
| Месяц | Остатки модели X*(t*) | Остатки модели Y(t) |
| 0,20 | –0,17 | |
| 0,06 | –0,02 | |
| –0,06 | –0,04 | |
| 0,12 | –0,07 | |
| 0,06 | 0,13 | |
| 0,03 | 0,28 | |
| 0,38 | 0,41 | |
| –0,52 | –0,11 | |
| –0,19 | –0,26 | |
| –0,13 | –0,17 | |
| 0,002 | –0,04 |
Параметры модели ΔY = f(ΔХ*) представлены в таблице 39.
Таблица 39 – Результаты расчета параметров модели ΔY = f(ΔХ*)
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | –0,01 | 0,04 | –0,27 | 0,79 |
| Переменная ΔХ* | 0,61 | 0,18 | 3,41 | 0,002 |
Проверка статистической значимости коэффициентов модели (см. тему 1) показывает, что модель требует уточнения.
Параметры уточненной модели ΔY = f(ΔХ*) представлены в таблице 40.
Таблица 40 – Результаты расчета параметров уточненной модели ΔY = f(ΔХ*)
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Переменная ΔХ* | 0,61 | 0,17 | 3,51 | 0,002 |
| Y-пересечение | #Н/Д | #Н/Д | #Н/Д |
В модели ΔY = 0,61ΔХ* автокорреляция отсутствует (таблица 41).
Таблица 41 – Анализ модели по отклонениям на наличие автокорреляции
остатков
| Коэффициент корреляции остатков | 0,20 |
| tнабл | 0,9 |
| tкр | 2,09 |
Прогнозирование. Из уравнения модели Х = 0,19 t + 8,61 для Х = 15 находится значение t = 33,53.
|
|
|
Используя авторегрессионое преобразование первого порядка AR(1) 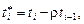 при r = 0,746, ti = 33,53, ti –1 = 32,53 находится t * = 9,25. По модели X* = 0,19 t * + 2,18 вычисляется Х* модельное, равное 3,98. Для нахождения Х*набл используется авторегрессионное преобразование первого порядка AR(1)
при r = 0,746, ti = 33,53, ti –1 = 32,53 находится t * = 9,25. По модели X* = 0,19 t * + 2,18 вычисляется Х* модельное, равное 3,98. Для нахождения Х*набл используется авторегрессионное преобразование первого порядка AR(1) 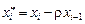 = 15 –
= 15 –
– 0,75*14,81 = 3,94, где 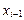 рассчитывается по модели Х = 0,19 t + 8,61 при t– 1 = 32,53,
рассчитывается по модели Х = 0,19 t + 8,61 при t– 1 = 32,53, 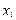 = 15 (из условия). Отклонение по фактору Х определяется как разность между наблюдаемым и модельным значениями
= 15 (из условия). Отклонение по фактору Х определяется как разность между наблюдаемым и модельным значениями
ΔХ* = Х*набл – Х*модельное = – 0,03.
Используя модель ΔY = 0,61ΔХ*, находится ΔY = 0,61*(– 0,03) =
= – 0,02. По модели Y = 5,22 + 0,07 t при t = 33,5 находится прогнозируемое значение Y = 7,62. С учетом исключения трендов прогнозируемое значение Y = 7,62 – 0,02 = 7,6.
Все вычисления занесены в таблицу 42.
Таблица 42 – Вычисление прогнозного значения
| t находится по модели X(t) при Х = 15 | 33,53 |
| t * находится из AR(1) | 9,25 |
| Х*модельное находится по модели Х*(t *) | 3,98 |
| Х при t –1 по модели Х(t) | 14,81 |
| Х из условия | |
| Х* набл, используя AR(1) | 3,94 |
| Отклонение Δ x * | –0,03 |
| Остаток по модели по отклонениям | –0,02 |
| Y прогнозируемый по модели Y(t) | 7,62 |
| Y прогнозируемый с учетом исключения трендов | 7,60 |
Вопросы для самоконтроля
1. Что понимают под ложной корреляцией?
2. Какова суть метода отклонений от тренда?
3. В каком случае используется ОМНК?
4. Каковы основные этапы ОМНК?
5. Как осуществляется прогнозирование?
 2015-05-18
2015-05-18 661
661








