Вначале обратимся к вопросу о тесноте линейной связи двух переменных. Предположим, что между переменными X и Y существует линейная связь.
В качестве меры для степени линейной связи двух переменных используется коэффициент их корреляции. Приведем вначале формулу выборочного коэффициента корреляции переменных X и Y.
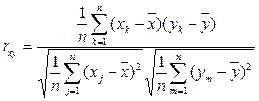 , (1)
, (1)
где n объем выборки.
Коэффициент парной корреляции rxy может быть рассчитан и по другим формулам, например:
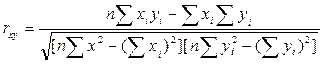 , (2)
, (2)
Для выявления корреляции проводят некоторое количество опытов (наблюдений) на случайными величинами X и Y, в результате чего получается ряд из пар реализаций, которые могут быть сведены в таблицу (табл.1).
Таблица 1
Данные наблюдений
| xi | x1 x2 … xn |
| yi | y1 y2 … yn |
При этом одному и тому же значению случайной величины X может соответствовать несколько различных значений случайной величины Y и наоборот.
Графическое представление результатов – это изображение пар (xi; yi) точками в декартовой системе координат. Полученный точечный график называется полем рассеивания, или корреляционным полем.
На рис 1. изображено корреляционное поле, характеризующее зависимость производительности труда (руб./чел.-ч.) от электровооруженности.
  |
Рис. 1. Корреляционное поле (прямая корреляция.
На рис.2. изображено корреляционное поле зависимости производительности труда от брака продукции.
  |
Рис. 2. Корреляционное поле (обратная корреляция)
Ряд значений может быть также интервальным. В этом случае он содержит не точечные значения Xi и Yi, а интервалы D Xi и D Yi или средние значения 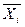 и
и 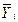 , где i – номера интервалов.
, где i – номера интервалов.
Имея ряды значений переменных X и Y, рассчитывают коэффициент парной корреляции rxy для решения вопроса о том, связаны ли между собой линейно переменные X и Y.
Коэффициент корреляции имеет следующие свойства:
· коэффициент корреляции является безразмерной величиной (так как размерности числителя и знаменателя есть размерности произведения XY); его величина не зависит от выбора единиц измерения обеих переменных;
· значение коэффициентов парной корреляции лежит в интервале от –1 до +1. Положительное его значение свидетельствует о прямой связи, отрицательное - об обратной, т.е. когда растет одна переменная, другая уменьшается. Чем ближе его значение к единице, тем теснее связь. Считается, что связь достаточно сильная, если коэффициент корреляции по абсолютной величине превышает 0,7, и слабая, если он меньше 0,3.
· близкая к нулю величина коэффициента корреляции говорит об отсутствии линейной связи переменных, но не об отсутствии связи между ними вообще. Это ясно из правой части рис. 3, где X и Y, очевидно, связаны друг с другом (лежат на одной окружности), но их коэффициент корреляции близок к нулю. Последнее вытекает из того, что каждой паре одинаковых отклонений переменной X от ее среднего значения соответствуют равные по абсолютной величине положительное и отрицательное отклонения переменной Y от ее среднего. Соответственно, произведения этих отклонений "гасят" друг друга в числителе формулы коэффициента корреляции, и он оказывается близким к нулю.
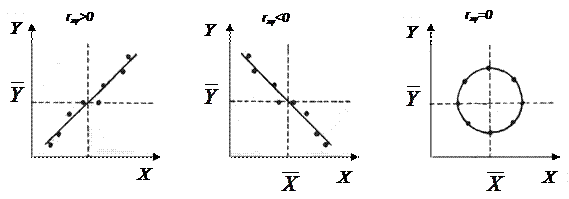 |
Рисунок 3. Типы зависимостей и коэффициент корреляции
А как же измеряется теснота нелинейной связи показателей?
Рассмотренный коэффициент корреляции rxy показывает тесноту связи лишь в случае линейной зависимости между случайными величинами, имеющими совместное нормальное распределение. Поэтому возникает необходимость иметь коэффициенты тесноты, или интенсивности, связи и в случае нелинейной зависимости. Роль таких коэффициентов играют корреляционное отношение и индекс корреляции, а также коэффициент детерминации. Эти показатели являются универсальными, так как подходят для измерения тесноты как нелинейной, так и линейной связи. Однако для расчета любого из универсальных показателей нужна конкретная корреляционная модель. Расчет универсальных показателей проводят после того, как такая модель будет выбрана и будут оценены ее параметры (см. 2.3.3.) и станет возможным получение по модели расчетных значений 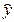 .
.
Рассмотрим указанные универсальные показатели.
1. Корреляционным отношением (эмпирическим) называется величина
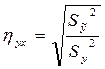 (3)
(3)
где 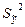 - выборочная дисперсия расчетных значений
- выборочная дисперсия расчетных значений 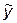 вычисленных по уравнению регрессии (нелинейному или линейному), а
вычисленных по уравнению регрессии (нелинейному или линейному), а 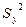 - полная дисперсия для эмпирических значений y.
- полная дисперсия для эмпирических значений y.
Дисперсия в числителе выражает вариацию, обусловленную выбранным фактор-признаком х, или это есть дисперсия, объясненная уравнением регрессии. Полная же дисперсия, стоящая в знаменателе, помимо фактора х обуславливается еще и многими другими факторами, не учтенными в модели.
Если 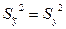 , т.е. теоретически рассчитанные значения показателя y по уравнению регрессии совпадают с эмпирическими данными, то
, т.е. теоретически рассчитанные значения показателя y по уравнению регрессии совпадают с эмпирическими данными, то 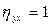 , если же
, если же 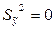 , то переменная х не вызывает изменения
, то переменная х не вызывает изменения 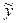 и
и 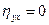 .
.
2. Наряду с корреляционным отношением в математической статистике используют индекс корреляции.
Как уже отмечалось, дисперсию 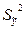 называют объясненной дисперсией, а дисперсию
называют объясненной дисперсией, а дисперсию 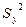 - полной. Имеет место равенство
- полной. Имеет место равенство 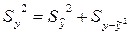 , которое вытекает из равенства
, которое вытекает из равенства
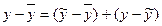
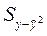 - остаточная (необъясненная) дисперсия, т.е. вариация разностей между эмпирическими данными и линией регрессии.
- остаточная (необъясненная) дисперсия, т.е. вариация разностей между эмпирическими данными и линией регрессии.
Если в формуле (3) представить объясненную дисперсию 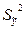 как разность между полной дисперсией
как разность между полной дисперсией 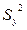 случайной величины y и необъясненной (остаточной дисперсией)
случайной величины y и необъясненной (остаточной дисперсией) 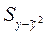 , то получим формулу для расчета так называемого индекса корреляции:
, то получим формулу для расчета так называемого индекса корреляции:
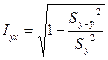 (4)
(4)
Для вычисления остаточной и полной дисперсий используются формулы
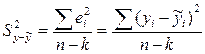 (5)
(5)
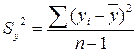 (6)
(6)
где n – объем выборки (количество наблюдений), к – количество неизвестных параметров в уравнении регрессии.
В случае парной корреляции неизвестных параметров в уравнении регрессии всего два, a0 и a1, и потому к=2.
3. Величина 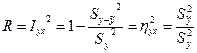 называется коэффициентом детерминации. Коэффициент детерминации показывает, какая часть дисперсии случайной величины y объясняется построенным уравнением регрессии.
называется коэффициентом детерминации. Коэффициент детерминации показывает, какая часть дисперсии случайной величины y объясняется построенным уравнением регрессии.
Чем ближе коэффициент детерминации R к единице, тем меньше остаточная, или необъясненная, дисперсия 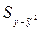 и следовательно, тем лучше построенное уравнение регрессии отражает корреляционную зависимость между показателями х и y.
и следовательно, тем лучше построенное уравнение регрессии отражает корреляционную зависимость между показателями х и y.
Для линейной модели регрессии коэффициент корреляции rxy, корреляционное отношение 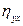 и индекс корреляции Iyх численно равны между собой. В случае нелинейной модели коэффициент корреляции rxy может быть близок или даже равен нулю, а коэффициенты
и индекс корреляции Iyх численно равны между собой. В случае нелинейной модели коэффициент корреляции rxy может быть близок или даже равен нулю, а коэффициенты 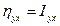 могут быть близки к единице или даже равны единице в случае удачного выбора нелинейной зависимости y от x. Равенство индекса корреляции или коэффициента детерминации единице означает функциональную зависимость y от x.
могут быть близки к единице или даже равны единице в случае удачного выбора нелинейной зависимости y от x. Равенство индекса корреляции или коэффициента детерминации единице означает функциональную зависимость y от x.
2.1.3. Спецификация и параметризация однофакторного уравнения регрессии
Уравнение регрессии – это формула статистической связи между переменными. Если эта формула линейна, то речь идет о линейной регрессии. Формула статистической связи двух переменных называется парной регрессией. Например, Кейнсом была предложена линейная формула зависимости частного потребления С от располагаемого дохода 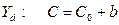 .
. 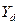 , где
, где 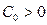 - величина автономного потребления, 1>b>0 – предельная склонность к потреблению.
- величина автономного потребления, 1>b>0 – предельная склонность к потреблению.
Выбор формулы связи переменных называется спецификацией уравнения регрессии. Оценка значений параметров выбранной формулы статистической связи переменных называется параметризацией уравнения регрессии.
Как же провести спецификацию модели? Рассмотрим вначале рис.4.
 |  | ||||
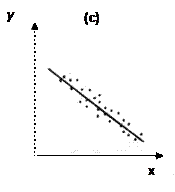 |
Рисунок 4. Графики взаимосвязи переменных
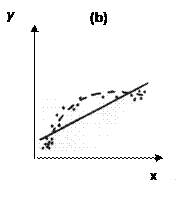
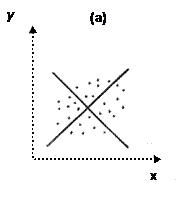
На рисунке 4 изображены три ситуации:
· на графике (а) взаимосвязь x и y близка к линейной: прямая линия (1) здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий;
· на графике (b) реальная взаимосвязь величин х и у описывается нелинейной функцией (2), и какую бы мы ни провели прямую линию (например, 1), отклонения точек наблюдений от нее будут существенными и неслучайными;
· на графике (с) реальная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, прямые линии 1 и 2, проведенные через "центр" "облака" точек наблюдений и имеющие противоположный наклон, одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х.
По виду эмпирической ломаной линии регрессии или же путем визуального анализа корреляционного поля можно определить форму плавной линии, определяющую основную тенденцию статистической зависимости.
Если это прямая линия, то линия регрессии имеет вид (а0+а1х). Однозначно в пользу линейного уравнения регрессии говорит и высокое значение выборочного коэффициента корреляции 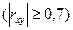 , рассчитываемого по исходному ряду значений переменных Х и Y.
, рассчитываемого по исходному ряду значений переменных Х и Y.
Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Если имеется некоторое "облако" точек наблюдений, через него всегда можно попытаться провести некоторую прямую линию, т.е. предположить линию регрессии вида (а0+а1 .х), даже если выборочный коэффициент парной корреляции по абсолютной величине много меньше 0,7.
Лишь в случае 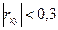 линейное уравнение безусловно непригодно. В этом случае нужно предполагать нелинейную связь и по виду корреляционного поля подбирать то или иное нелинейное уравнение регрессии.
линейное уравнение безусловно непригодно. В этом случае нужно предполагать нелинейную связь и по виду корреляционного поля подбирать то или иное нелинейное уравнение регрессии.
Окончательный ответ о правильности выбора уравнения регрессии дает проверка модели на адекватность, проводимая после расчета параметров выбранной формулы статистической связи переменных.
Для оценивания параметров уравнения регрессии используется метод наименьших квадратов (МНК). МНК – это метод оценивания параметров уравнения регрессии, минимизирующий сумму квадратов отклонений фактических значений  (из ряда наблюдений) от значений
(из ряда наблюдений) от значений  , вычисленных по уравнению регрессии.
, вычисленных по уравнению регрессии.
Математически:
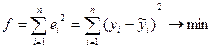 (5)
(5)
Берем квадраты отклонений, а не просто отклонения, потому что отклонения могут быть положительными и отрицательными, а их сумма может быть равна нулю для многих кривых, в том числе и для кривых, которые отражают зависимость очень плохо.
Проиллюстрируем определение методом наименьших квадратов параметров линейного уравнения регрессии.
Прямых линий регрессии с уравнением 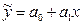 , аппроксимирующих точки корреляционного поля и отображающих графический ряд наблюдений (хi, уi), можно построить много. Коэффициент а0 равен длине отрезка, отсекаемого прямой на оси Y, а коэффициент а1 характеризует наклон прямой к оси Х.
, аппроксимирующих точки корреляционного поля и отображающих графический ряд наблюдений (хi, уi), можно построить много. Коэффициент а0 равен длине отрезка, отсекаемого прямой на оси Y, а коэффициент а1 характеризует наклон прямой к оси Х.
Изменяя эти коэффициенты, получим целое семейство прямых, каждая из которых приближается к исходным точкам корреляционного поля (рис. 5).
Рисунок 5. Семейство прямых с различным углом наклона
Из всего этого семейства нужно выбрать одну, наилучшую, прямую. Критерием по которому отыскивается наилучшая прямая является сумма квадратов отклонений фактических значений уi из ряда наблюдений от значений 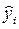 , вычисленных по уравнению прямой.
, вычисленных по уравнению прямой.
Обозначим через еi указанные выше отклонения, тогда критерий выбора подходящей прямой можно записать так:
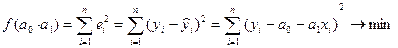 (6)
(6)
Функция 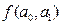 является функцией переменных а0 и а1, и точка ее минимума должна удовлетворять условиям
является функцией переменных а0 и а1, и точка ее минимума должна удовлетворять условиям
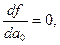
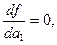 (7)
(7)
Беря частные производные, получим следующую систему так называемых нормальных уравнений:
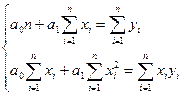 (8)
(8)
Решение этой системы относительно искомых параметров дает следующие выражения:
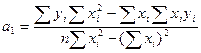 (9)
(9)
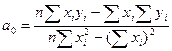
или
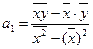 .
. 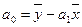 (10)
(10)
Коэффициент а1 называется коэффициентом регрессии.
Коэффициент регрессии а1 показывает, на сколько единиц в среднем изменяется результативный показатель у при увеличении фактора-признака х на одну единицу.
На рис. 6 показана выбранная по методу наименьших квадратов прямая линия для некоторых пар наблюдений (хi, уi), 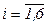 .
.
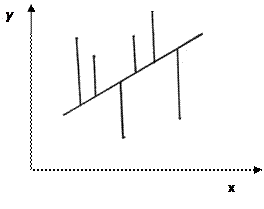
Рисунок 6. Подбор прямой по методу наименьших квадратов
Здесь показаны вертикальные отклонения от прямой, как положительные (для точек сверху прямой), так и отрицательные (для точек снизу прямой), причем сумма квадратов всех отклонений оказывается минимальной.
2.1.4. Пример расчета линейной модели регрессии
Рассмотрим пример. Пусть имеются данные о товарообороте и сумме издержек обращения по 10 магазинам в млн. руб.
Таблица 2
| Товарооборот | ||||||||||
| Издержки обращения |
Из табл. 2 видно, что с увеличением товарооборота увеличиваются в общем и издержки обращения.
Согласно формуле (2), коэффициент корреляции в нашем примере может быть вычислен по следующей схеме (табл. 3.)
Таблица 3
| Товарооборот X | Издержки обращения Y | x1*y1 | x12 | y12 |
| 14 400 | 230 400 | |||
| 12 750 | 260 100 | |||
| 16 430 | 280 900 | |||
| 15 120 | 291 600 | |||
| 16 530 | 324 900 | |||
| 18 880 | 348 100 | |||
| 22 320 | 384 400 | |||
| 23 040 | 409 600 | |||
| 24 050 | 422 500 | |||
| 25 080 | 435 600 | |||
| Итого: 5790 | 188 600 | 3 388 100 | 10 540 |
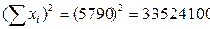
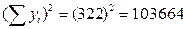
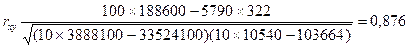
 2015-05-18
2015-05-18 8522
8522
