Этапы построения многофакторной модели

Значения экономических переменных определяются обычно влиянием не одного, а нескольких объясняющих факторов. В таком случае зависимость Y=f(X) означается, что X – вектор, содержащий m компонентов: X=(X₁, X₂, …, X_m). Задача оценки статистической взаимосвязи переменных Y и X=(X₁, X₂, …, X_m) формулируется аналогично случаю парной регрессии.

Связь между зависимой переменной Y и m независимыми факторами можно охарактеризовать функцией регрессии Y=f(X₁, X₂, …, X_m), которая показывает, каким будет в среднем значение переменной Y, если переменные X примут конкретное значение. Это обстоятельство позволяет применять модель регрессии не только для анализа, но и для прогнозирования.

Множественная корреляция и регрессия определяют форму связи переменных, выявляют тесноту их связи и устанавливают влияние отдельных факторов.

Основными этапами построения регрессионной модели являются:

· отбор факторов для модели, сбор и предварительный анализ исходных данных;

· выбор вида модели и численная оценка ее параметров;

· проверка качества модели;

· оценка влияния отдельных факторов на основе модели;

· прогнозирование на основе модели регрессии;

Рассмотрим содержание этих этапов и их реализацию.

2.2.2. Отбор факторов для модели. Сбор и предварительный анализ данных

Информационной базой регрессионного анализа являются многомерные временные ряды, каждый из которых отражает динамику одной переменной и должен удовлетворять изложенным выше требованиям статистического аппарата исследования.

Выбор факторов, влияющих на исследуемый показатель, производится прежде всего исходя из содержательного экономического анализа.

Для получения надежных оценок в модель не следует включать слишком много факторов. Их число не должно превышать одной трети объема имеющихся данных (т.е. m<=N/3).

Для определения наиболее существенных факторов могут быть использованы коэффициенты линейной и множественной корреляции, детерминации и частные коэффициенты корреляции.

Коэффициенты парной (линейной) корреляции особенно полезны при построении простых моделей. При наличии двух факторов они вычисляются по формулам:

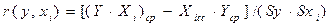; (18)

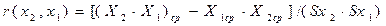; (19)

где Y_ср – среднее значение зависимой переменной;

Х_ср – среднее значение фактора j;

(…)_ср – среднее значение из суммы произведений двух переменных;

Sy – среднее квадратическое отклонение Y;

Sx - среднее квадратическое отклонение X.

Значение коэффициентов парной корреляции лежит в интервале от –1 до +1. Его положительное значение свидетельствует о прямой связи, отрицательное – об обратной, т.е. когда растет одна переменная, другая уменьшается. Чем ближе его значение к 1, тем теснее связь. Считается, что связь достаточно сильная, если коэффициент корреляции по абсолютной величине превышает 0,7, и слабой, если меньше 0,3. При равенстве его нулю связь полностью отсутствует. Этот коэффициент дает объективную оценку тесноты связи лишь при линейной зависимости переменных.

Коэффициент множественной корреляции, который принимает значение от 0 до 1, более универсальный: чем ближе его значение к 1, тем в большей степени учтены факторы, влияющие на зависимую переменную, тем более точной может быть модель.

Рассмотренные показатели во многих случаях не дают однозначного ответа на вопрос о наборе факторов. Поэтому в практической работе с использованием ПЭВМ чаще осуществляется отбор факторов непосредственно в ходе построения модели методом пошаговой регрессии.

Суть метода состоит в последовательном включении факторов. На первом шаге строится однофакторная модель с фактором, имеющим максимальный коэффициент парной корреляции с результативным признаком. Вычисляется необъясненная дисперсия. Вторым в модель включается фактор с максимальным среди оставшихся факторов коэффициентом корреляции. В результате включения нового фактора в модель снижается необъясненная дисперсия. Дальнейшее включение в модель все большего числа факторов, проранжированных по убыванию коэффициента корреляции с результирующим признаком, ведет к постоянному снижению доли необъясненной факторами дисперсии.

При включении новой переменной в модель рассчитывается величина C(j), равная относительному уменьшению суммы квадратов отклонений зависимой переменной от фактически наблюденных значений, возникающему за счет включения нового фактора в модель.

Величина C(j) интерпретируется как доля оставшейся дисперсии независимой переменной, которую объясняет зависимая переменная j.

Остаточной дисперсией называется та часть вариации зависимой переменной, которую нельзя объяснить воздействием объясняющих переменных (факторов). Именно поэтому она используется как для оценки качества модели и ее точности, так и для полноты набора объясняющих переменных (факторов).

Пусть на очередном шаге к номер переменной, включаемой в модель, соответствует j. Если С_к меньше заранее заданной константы, характеризующей уровень отбора, то построение модели прекращается. В противном случае к -тая переменная вводится в модель.

2.2.3. Выбор вида модели и оценка ее параметров

Для отображения зависимости переменных могут использоваться показательная, параболическая и многие другие функции. Однако в практической работе наибольшее распространение получили модели линейной зависимости, т.е. когда факторы входят в модель линейно.

Линейная модель множественной регрессии, которая строится на основе временных рядов наблюдений, имеет вид:

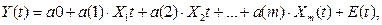(20)

где Y(t) – зависимая переменная (основной показатель);

Х(t) – независимые переменные (факторы);

t – порядковый номер наблюдения временного ряда (t=1,2…N);

a(j) – коэффициенты регрессии (j=0…m), подлежащие численному оцениванию на основе N наблюдений и m факторов;

E(t) – остаточная компонента, дисперсия которой также должна быть оценена.

Параметры модели оцениваются по МНК. Для двухпараметрической модели система нормальных уравнений, из которой определяются коэффициенты регрессии, имеет вид:

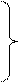
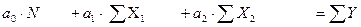
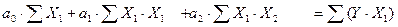(21)

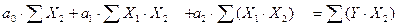
Здесь и далее суммирование ведется по числу наблюдений N.

Эту систему с тремя неизвестными коэффициентами регрессии можно решить методом Гаусса, по формулам Крамера или любым другим способом.

Если записать выражение для определения коэффициентов регрессии в матричной форме, то становится очевидным, что решение задачи возможно лишь тогда, когда столбцы и строки матрицы исходных данных независимы. Для экономических показателей это условие выполняется не всегда. Линейная или близкая к ней связь между факторами называется коллиниарностью и приводит к линейной зависимости нормальных уравнений, что делает вычисление параметров либо невозможным, либо затрудняет содержательную интерпретацию параметров модели. Чтобы избавиться от коллиниарности, в модель включают лишь один из линейно связанных между собой факторов, причем тот, который в большей степени связан с зависимой переменной.

2.2.4. Проверка качества модели

Качество модели оценивается стандартным для математических моделей образом: по адекватности и точности. Расчетные значения получаются путем подстановки в модель фактических значений всех включенных факторов.

Для проверки адекватности модели регрессии используется F -значение, вычисляемое как отношение дисперсии исходного ряда и несмещенной дисперсии остаточной компоненты. Если расчетное значение с 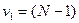и 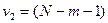степенями свободы больше табличного при заданном уровне значимости, то модель считается адекватной.

В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине 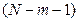. Квадратный корень из этой величины (S_e) называется стандартной ошибкой оценки.

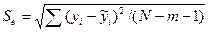(22)

О тесноте связи факторов в модели, а также ее точности, можно судить по величине таких характеристик, как корреляционное отношение, индекс корреляции, коэффициент детерминации.

Так, коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов. Чем ближе этот коэффициент к 1, тем точнее построенная модель.

Целесообразно проанализировать также значимость отдельных коэффициентов регрессии. Это осуществляется по t – статистике путем проверки гипотезы о равенстве нулю к -го параметра уравнения (кроме свободного члена):

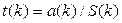(23)

где S(к) – это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии а(к).

Если расчетное значение t – критерия с 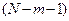степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).

2.2.5. Оценка влияния отдельных факторов на основе модели

Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности Э(j) и бета-коэффициенты 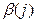, которые рассчитываются соответственно по формулам:

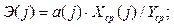(24)

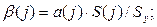(25)

где S(j) – среднеквадратическое отклонение фактора j.

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора j на один процент. Однако он не учитывает степень колеблемости факторов.

Бета-коэффициент показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением соответствующей независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.

Указанные коэффициенты позволяют проранжировать факторы по степени влияния факторов на зависимую переменную.

Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов D(j):

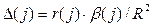, (26)

где r(j) – коэффициент парной корреляции между фактором j(j=I,…m) и зависимой переменной;

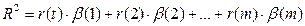. (27)

При корректно проводимом анализе все b -коэффициенты положительны.

2.2.6. Прогнозирование на основе модели регрессии

При использовании построенной модели для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных.

Для прогнозирования зависимой переменной на к шагов вперед необходимо знать прогнозные значения всех входящих в нее факторов. Их оценки могут быть получены на основе временных экстраполяционных моделей или заданы пользователем. Эти оценки подставляются в модель и получаются прогнозные оценки.

Для получения интервального прогноза необходимо определить доверительный интервал.

Для линейной модели регрессии доверительный интервал рассчитывается следующим образом. Оценивается величина отклонения от линии регрессии (обозначим ее U):

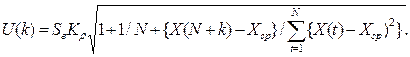(28)

Коэффициент K_p является табличным значением t – статистики Стьюдента при заданном уровне значимости и числа наблюдений. Если исследователь задает уровень вероятности попадания прогнозируемой величины внутрь доверительного интервала, равный 70%, то K_p=1,05. Если 95%, то K_p=1,96, а при 99% - K_p=2,65.

Как видно из формулы (28) величина U прямо пропорционально зависит от точности модели, коэффициента доверительной вероятности K_p, степени удаления прогнозной оценки фактора X от среднего значения и обратно пропорциональна объему наблюдений.

В результате получаем следующий интервал прогноза для шага прогнозирования к:

· верхняя граница прогноза =Y(N+к)+U(к),

· нижняя граница прогноза =Y(N+к)-U(к).

Если построенная регрессионная модель адекватна и прогнозные оценки факторов достаточно надежны, то с выбранной пользователем вероятностью можно утверждать, что при сохранении сложившихся закономерностей развития прогнозируемая величина попадет в интервал, образованный нижней и верхней границами.