Зависимость между теми или иными факторами в эконометрике не всегда можно описать с помощью линейной функции. В этом случае применяют нелинейную регрессию. Общий вид:
yрасч=f(x1) – для однофакторной регрессии
yрасч=f(x1,x2,…,xp) – для многофакторной регрессии
| a>1 |
| a<1 |
Для перехода к линейному виду, уравнение логарифмируют по основанию a:
logay=logaabx+ε=bx+ ε
logay=bx+ ε
Заменим зависимую переменную logay на z:
z= bx+ ε
Частный случай экспоненциальной зависимости – логистическая кривая:
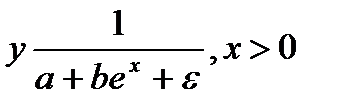
Данная кривая имеет 2 горизонтальные асимптоты y=o, y=1/a и точку перегиба 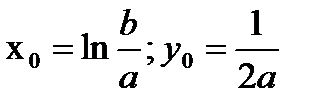
| 1/a 1/2a 1/(a+b) |
Логистические кривые используются для описания поведения показателей, имеющих определенные уровни насыщения (например, для описания зависимости спроса на товар от дохода).
Линеаризация этой зависимости проводится с помощью перехода к переменным
ex=t; 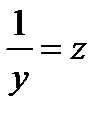 . Получаем: z=a+bt+ε
. Получаем: z=a+bt+ε
Зависимости логарифмического типа имеют вид 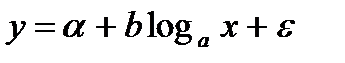
| a>1 |
| a<1 |
Обозначим logax=z. Получим линейную модель:
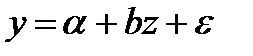
Зависимости полиномиального вида:
y=a+b1x+b2x2+…+bpxp+ε
Обозначим x=z1, x2=z2,…, xp=zp
y=a+b1z1+b2z2+…+bpzp+ ε
Зависимости степенного вида
y=axb
Прологарифмируем по основанию e:
ln(y)=ln(a)+b*ln(x)
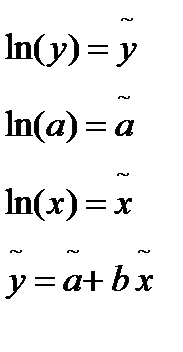
Если модель по независимым факторам является мультипликативной, то переход к аддитивной модели и как следствие к линейной осуществляется с помощью логарифмирования всей зависимости
3.1.2. Методы оценивания линеаризуемых функций:
Параметры нелинейной регрессии, линеаризуемой с помощью различных преобразований, оценивается МНК.
Для этого минимизируют функционал вида
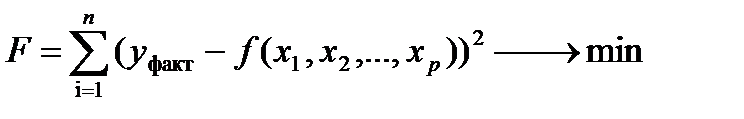 (3.1)
(3.1)
Рассмотрим на примере для оценки параметров кривой Филипса, определяющей нелинейное отношение между нормативами безработицы и относительными изменениями заработной платы.
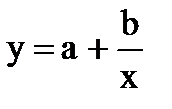 , где
, где
y – безработица
x – заработная плата
Для более легкой оценки заменим 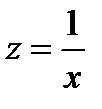
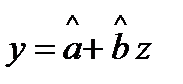
Получим функционал вида:
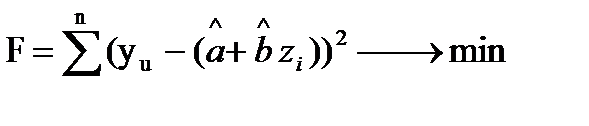
Чтобы определить тип данной функции и оценить параметры 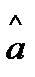 и
и 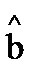 находят:
находят:
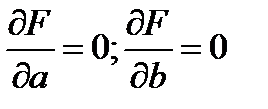
Затем делаем обратную замену z=1/x и получаем систему нелинейных уравнений
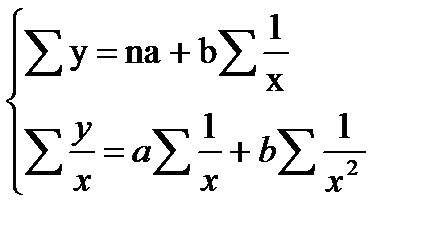
Разрешая систему относительно 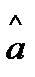 и
и 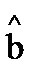 , получаем выражения для их оценок.
, получаем выражения для их оценок.
 2015-05-18
2015-05-18 324
324








