2015-05-18
285
Способ получения прогнозных значений объемов продаж, рассмотренный в первых трех задачах является не единственным. В зависимости от предпочтений исследователя можно сформулировать другие исходные предпосылки, выбрать другие математические функции, использовать другие методы оценки параметров и, наконец, можно оценивать параметры тренда и величину сезонных колебаний не по отдельности, а одновременно. Рассмотрим последний вариант более подробно, поскольку он в принципе ничем не отличается от рассмотренного выше способа, но с математической точки зрения представляет собой интересную альтернативу.
Предположим, что в течение последних трех лет и в ближайшем будущем году наблюдался и будет наблюдаться стабильный рост продаж с постоянным абсолютным приростом и постоянными сезонными колебаниями. Математически эти предпосылки можно формализовать с помощью следующей математической модели:
,
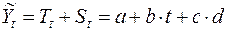где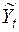 
– прогнозное значение объема продаж в момент времени 
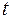, рассчитанное без учета случайной компоненты временного ряда; 
, 
, 
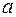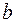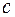– произвольные параметры модели, отражающие начальный уровень тренда, величину постоянного прироста и величину сезонных колебаний соответственно; 
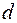– фиктивная переменная, принимающая значение 
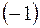, если объем продаж относится к первому полугодию года, и значение 
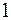, если объем продаж относится ко второму полугодию. Переменная 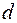называется фиктивной, потому что она является искусственно созданной для отражения факта принадлежности объемов продаж к одному из полугодий соответствующего года.
Смысл модели будет более понятен, если выразить с помощью нее прогнозные значения для первого и второго полугодия 2009г.:
, 
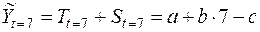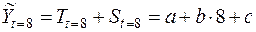
и сравнить их с выражениями (3) из второй задачи. Очевидно, что эти выражения полностью совпадают, если положить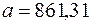 
, 
, 
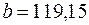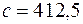. Разница заключается лишь в том, что в выражениях (3) задачи 2 оценка параметров 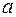и 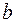осуществлялась отдельно от оценки величины сезонных колебаний 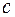, в то время как использование фиктивной переменной дает возможность провести эту оценку одновременно.
Итак, найдем оценки параметров 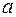, , 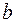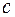с помощью метода наименьших квадратов. Поскольку в данной постановке задачи используются исходные данные, содержащие сезонность, то в отличие от задачи 2 здесь 
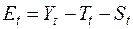, следовательно, для оценки параметров необходимо минимизировать следующую функцию:
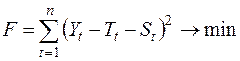
или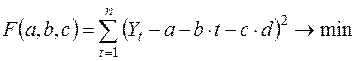 
Найдя три частные производные и приравняв их нулю, после ряда преобразований получаем следующую систему из трех линейных уравнений с тремя неизвестными:
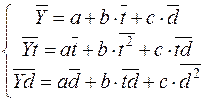. (4)
Используя исходные значения из таблицы 2 и присвоив фиктивной переменной значения 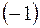и 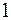в зависимости от соответствующих полугодий, рассчитаем все необходимые средние значения в таблице 9, при необходимости округляя получаемые значения до сотых.
Таблица 9
