2015-05-18
211
| Функция | Преобразования переменных | Преобразования коэффициентов | ||
| Y* | X* | A | B | |
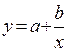
| y |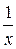 
| a | b |
| 
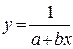
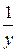
| x | a | b |
| 
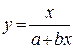
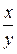
| x | a | b |
| 
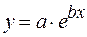
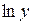
| x |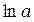 
| 
|
| 
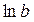
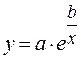
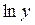
| x |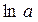 
| b |
|
| 
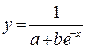
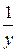
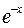
| a | b |
|
| 
| 
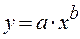
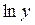
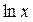
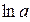
| b |
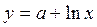
| y |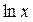
| a | b |
|
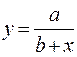
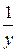
| x |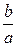 
| 
|
|
|
|
|
|
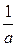
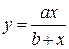
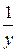
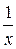
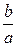
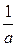
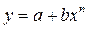
| y |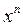 
| a | b |
4.2 Оценка качества нелинейной связи
При криволинейной зависимости в качестве меры тесноты связи между показателями х и у используется корреляционное отношение (или индекс корреляции). Индекс корреляции рассчитывается по формуле:
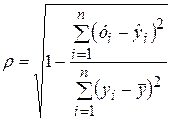(4.6)
Границы корреляционного отношения находятся в пределах от 0 до 1. Индекс корреляции следует рассматривать как показатель не только тесноты связи, но и степени близости линии регрессии к фактическим данным.
Также для анализа качества уравнения нелинейной регрессии можно использовать среднюю ошибку аппроксимации (см. формулу 2.9)
Статистическую значимость построенного уравнения нелинейной регрессии можно проверить с помощью F – критерия Фишера (см. формулу 3.7). Для оценки статистической значимости параметров нелинейной регрессии используют t – критерий Стьюдента (см. формулы 3.8 и 3.9)
Пример 1. По семи территориям Волжского региона за 2005 г. известны значения двух признаков (табл. 4.2.1).
Таблица 4.2.1
