Урок 5. Решение тригонометрических неравенств.
Урок рассчитан на 45 минут. Количество заданий и уровень их сложности учитель может изменить с учетом подготовленности класса.
Тип занятия: обобщение и систематизация знаний, умений и навыков, приобретенных при изучении данной темы.
Цели.
1. Образовательные: обобщение ЗУН, приобретенных при изучении данной темы.
2. Воспитательные: воспитывать культуру речи, аккуратность записей, самостоятельность.
3. Развивающие: развитие мышления, воображения, творческих способностей.
Оборудование: компьютер, мультимедийный проектор; карточки для основной части урока и домашнего задания.
Ход занятия.
| I. Организационный момент. | ||||||||||||||||||
II. Устная работа.
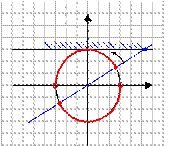
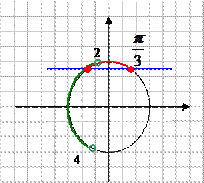
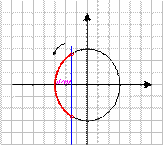
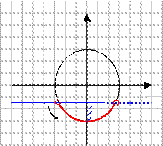
1) Поставьте в соответствие рисунок и неравенство, соответствующее множеству всех точек, изображенных на рисунке.
2) Решите неравенство:
| Слайд 2. Слайды 3, 4. | |||||||||||||||||
III. Решение задач.
№1.Решите неравенство 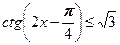 .
Решение. .
Решение.
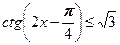 , ,
 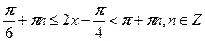 , ,
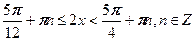 , ,
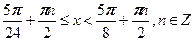 .
Ответ: .
Ответ: 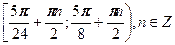 . .
| Тексты задач для урока – на карточках (приложение 1). Учащиеся самостоятельно решают задание в тетради, один человек работает у скрытой доски. После того, как решение окончено, выполнить проверку. | |||||||||||||||||
№2.Решите неравенство 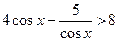 .
Решение. .
Решение.
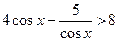 .
Обозначим .
Обозначим 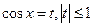 . .
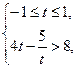
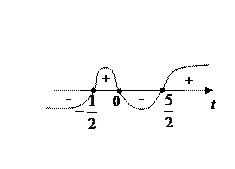 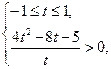
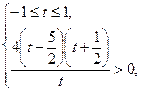
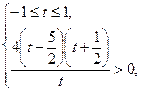
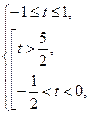
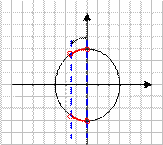 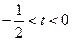 .
Вернемся к исходной переменной. .
Вернемся к исходной переменной.
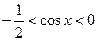 . .
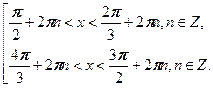 Ответ:
Ответ: 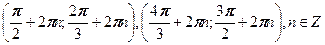 . .
| Совместное решение. Один человек решает неравенство у доски. | |||||||||||||||||
№3.Найдите область определения функции 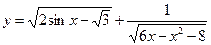 .
Решение. .
Решение.
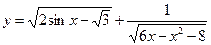 , ,
 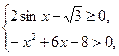
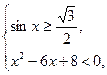
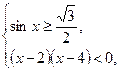
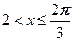 .
Ответ: .
Ответ: 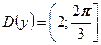
| Самостоятельно решить задание, после выполнить проверку (слайд 5). | |||||||||||||||||
№4.Найдите все значения x, при которых выполняется соотношение 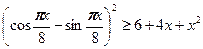 .
Решение. .
Решение.
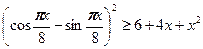 , ,
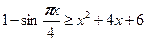 , ,
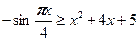 .
Оценим левую и правую части последнего неравенства. .
Оценим левую и правую части последнего неравенства.
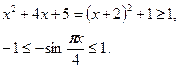 Следовательно, неравенство выполняется тогда и только тогда, когда выполняется система
Следовательно, неравенство выполняется тогда и только тогда, когда выполняется система
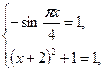
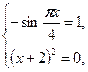
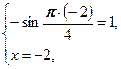
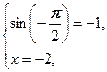
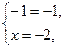
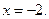 Ответ: Ответ: 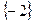 . .
| Совместное решение задачи, один ученик работает у доски. | |||||||||||||||||
| IV. Домашнее задание. Дети получают домашнюю самостоятельную работу, оценки за которую выставляются в журнал. | Приложение 2. |
Приложение 1.
№1.Решите неравенство 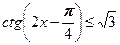 .
№2.Решите неравенство .
№2.Решите неравенство 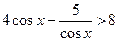 .
№3.Найдите область определения функции .
№3.Найдите область определения функции 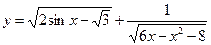 .
№4.Найдите все значения x, при которых выполняется соотношение .
№4.Найдите все значения x, при которых выполняется соотношение 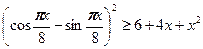 . .
|
Приложение 2.
Домашнее задание.
| 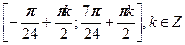
|
| 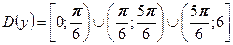
|
б) 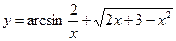 . .
| Ответ: 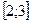
|
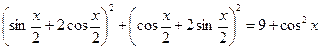
| Ответ: 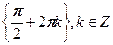
|
б) 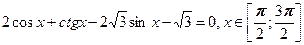
| Ответ: 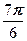
|
4. Найдите все решения уравнения 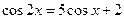 , удовлетворяющие условию: а) , удовлетворяющие условию: а) 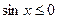 ; б) ; б) 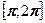 . .
|
а) 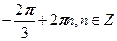 б)
б) 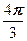 . .
|
5. Найдите все значения параметра а, при которых уравнение 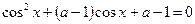 имеет на отрезке имеет на отрезке 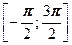 ровно три корня. Найдите эти корни. ровно три корня. Найдите эти корни.
| Если 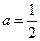 , то , то 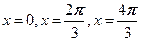 . Если . Если 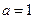 , то , то 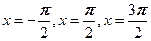
|
 2015-05-18
2015-05-18 444
444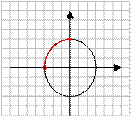
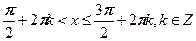
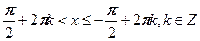
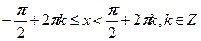
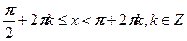
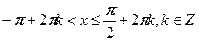
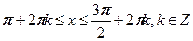
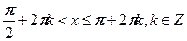
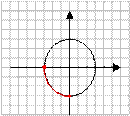
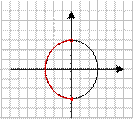
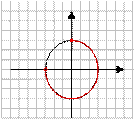
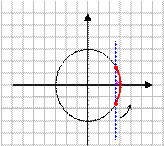 а)
а) 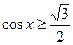
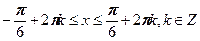
 б)
б) 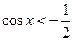
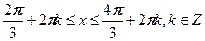
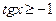
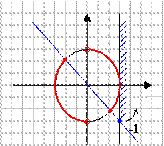
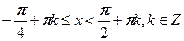
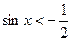
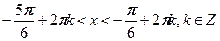
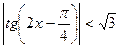 ;
; 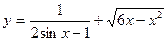 ;
;






