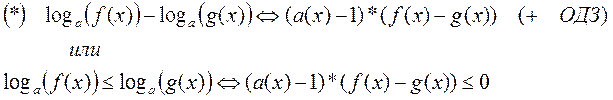 |
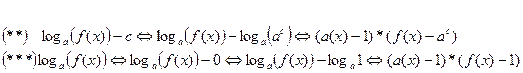 |
| 1. Смотрим на основания логарифмов. |
| Разные основания – привести к одному. |
2. Выражения, стоящие под знаком логарифма 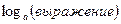 |
| Можно ли его разложить на множители или представить в виде дроби. |
| Применить ф(6 и 7) |
| 3. Если логарифмы стоят в степени или есть произведение логарифмов |
| Замена переменной или разложение на множители. |
Задачи части С3 ЕГЭ 2012-2014 годов





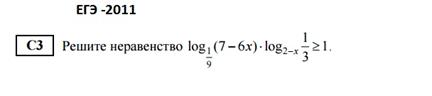
Задачи из сайта АЛЕКСЛАРИН
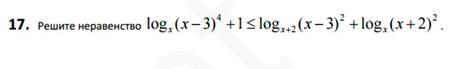
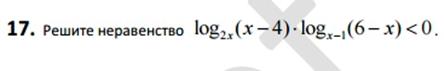
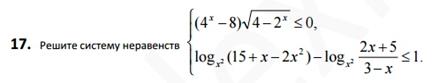
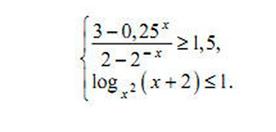 | 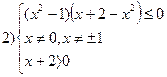 1) 1) 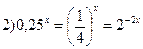 - затем замена переменных - затем замена переменных |
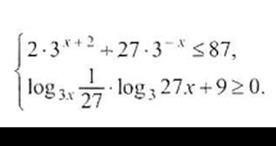 | 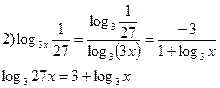 замена сведет неравенство к рациональному. замена сведет неравенство к рациональному. |
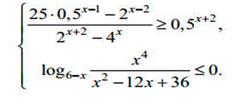 | 1) замена 2) Метод рационализации (см (***)) |
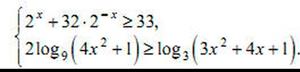 | 1) после замены сводится к квадратному неравенству 2) сводим к основанию 3 и получается простое лог. неравенство, решать, применяя равносильное преобразования |
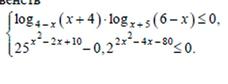 | 1) каждый логарифм заменяем на равносильное выражение по формуле рационализации (***) 2) свести к основанию 5 и виду 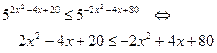 |
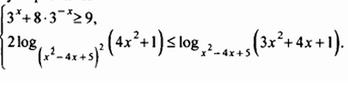 | 1) замена 2) применить слева формулу 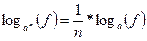 а затем Метод Рационализации (*) а затем Метод Рационализации (*) |
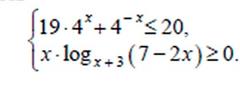 | 1) замена 2) Метод рационализации 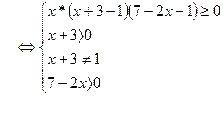 |
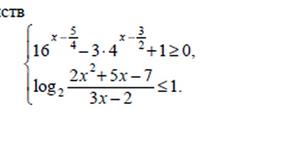 | 1)замена 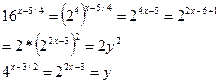 |
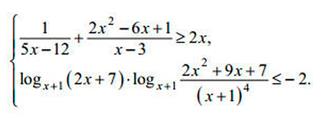 | 1) Рациональное неравенство, перенести все налево, привести к НОЗ, и решать методом интервалов 2) Второй логарифм представить в виде разности двух логарифмов (формула 7 из ТАБ.1) модулей не будет из-за ОДЗ. Трехчлен разложить на множители и еще раз применить формулу 6, в итоге, получится квадратное неравенство относительно логарифма. |
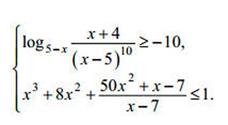 | 1) Можно сразу применить формулы рационализации, можно разложить на разность двух логарифмов и упростить. |
 2015-05-20
2015-05-20 4257
4257