2015-05-20
348
По гистограмме можно рассчитать значение моды для числового ряда. Для этого используется формула 1.
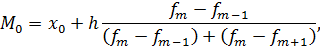
| (1) |
где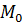 
– значение моды, 
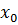– нижняя граница модального интервала, 
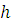– величина интервала, 
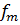– частота модального интервала, 
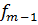– частота интервала, предшествующего модальному, 
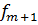– частота интервала, следующего за модальным. Модальный интервал – это тот интервал, которому соответствует наибольшая частота. В примере это интервал №4 (Таблица 6).
Таблица 6. – Модальный интервал соответствует наибольшей частоте.
| Номер интервала | Нижняя граница | Верхняя граница | Частота |
| -0,43 | 0,282 | ||
| 0,282 | 0,994 | ||
| 0,994 | 1,706 | ||
| 1,706 | 2,418 | ||
| 2,418 | 3,13 | ||
| Еще |
Таким образом,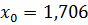 
, 
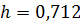(ширина одинакова для всех интервалов), 
, 
, 
.
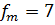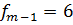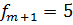Полученный по формуле результат (Рис. 17) отличается от результата, рассчитанного Excel в процедуре «Описательная статистика», потому что Excel лишь указывает повторяющиеся значения, не проводя группировку. По приведённой формуле моду можно найти всегда, даже если в исследуемом числовом ряду нет повторяющихся значений.
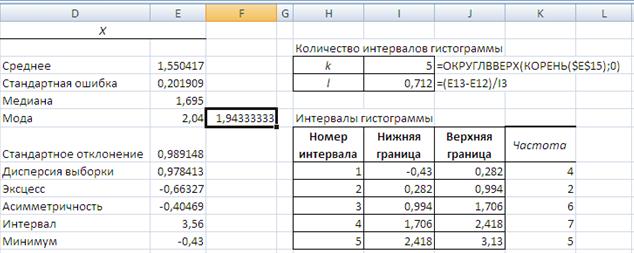
Рис. 17. Результат расчёта моды на данных примера.
