Найдём величину и направление вектора магнитной индукции в точке, находящейся на расстоянии Rот провода. Применим принцип суперпозиции
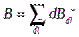 ,
,
где 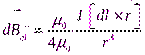 - вектор магнитной индукции, создаваемый элементом тока
- вектор магнитной индукции, создаваемый элементом тока 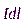 .
.
В 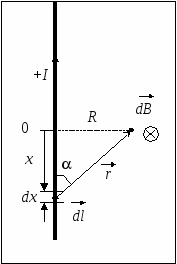 екторы
екторы 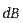 в выбранной точке от всех элементов
в выбранной точке от всех элементов 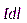 направлены одинаково (перпендикулярно плоскости, образованной векторами
направлены одинаково (перпендикулярно плоскости, образованной векторами 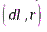 ), поэтому можно перейти от векторной суммы к сумме величин
), поэтому можно перейти от векторной суммы к сумме величин 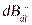 :
:
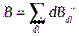 , где
, где 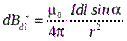 .
.
Введём координату х, отсчитываемую от точки пересечения провода и перпендикуляра к проводу, восстановленного из точки наблюдения. Тогда 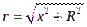 ,
, 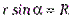 ,
, 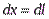 , поэтому
, поэтому
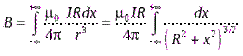 .
.
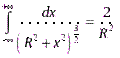 Но окончательно, величина индукции магнитного поля на расстоянии Rот тонкого длинного прямого провода с постоянным током I определяется соотношением:
Но окончательно, величина индукции магнитного поля на расстоянии Rот тонкого длинного прямого провода с постоянным током I определяется соотношением:
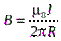
 .
.
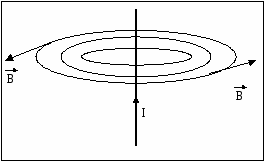
Силовые линии магнитного поля, создаваемого током в бесконечно длинном прямом проводнике, представляют собой окружности, лежащие в плоскости, перпендикулярной проводу, и с центром на оси провода. Направление вектора 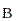 определяется по правилу правого винта. (Или правой руки: если обхватить правой рукой провод так, чтобы большой палец был направлен по току, то остальные пальцы покажут направление «закрученности» В.)
определяется по правилу правого винта. (Или правой руки: если обхватить правой рукой провод так, чтобы большой палец был направлен по току, то остальные пальцы покажут направление «закрученности» В.)
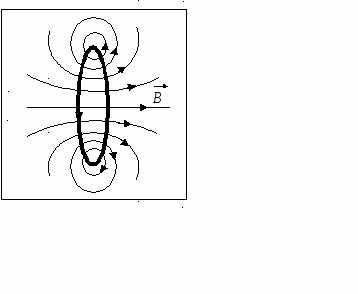
2) Рассмотрим магнитное поле, создаваемое круговым контуром с постоянным током, на оси контура.
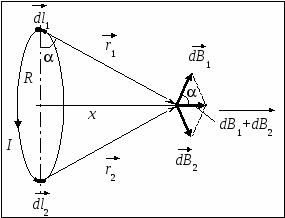 По контуру течёт ток силой I, радиус контура R. Найдём величину индукции магнитного поля в точке, находящейся на расстоянии x от плоскости контура вдоль его оси.
По контуру течёт ток силой I, радиус контура R. Найдём величину индукции магнитного поля в точке, находящейся на расстоянии x от плоскости контура вдоль его оси.
Любые два элемента 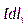 и
и 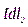 , расположенные симметрично относительно центра контура, создают в точке наблюдения два симметричных (относительно оси) вектора
, расположенные симметрично относительно центра контура, создают в точке наблюдения два симметричных (относительно оси) вектора 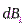 и
и 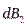 . Сумма этих векторов лежит на оси контура. Поэтому при нахождении суперпозиции всех векторов
. Сумма этих векторов лежит на оси контура. Поэтому при нахождении суперпозиции всех векторов 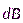 надо учитывать только проекцию векторов на эту ось:
надо учитывать только проекцию векторов на эту ось:
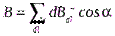 .
.
Т.к. образующая конуса перпендикулярна касательной к основанию, то угол между векторами 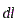 и
и 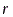 - прямой, поэтому
- прямой, поэтому
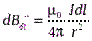 .
.
Для всех элементов 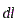 величины
величины 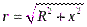 и
и 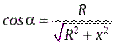 одинаковые. Следовательно,
одинаковые. Следовательно,
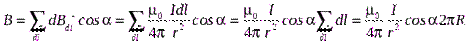 или
или
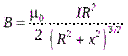
 .
.
С учётом определения магнитного момента контура 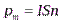 и величины площади круга
и величины площади круга 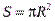 можно записать эту формулу в виде
можно записать эту формулу в виде
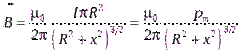 .
.
 2015-05-20
2015-05-20 933
933








