6.1. Класичний метод визначення екстремуму
Приклад 6.1. 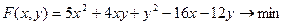
Розв’язок:
1. Знайдемо стаціонарні точки:
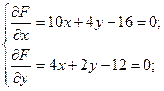
Розв’язком системи рівнянь є точка 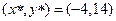 .
.
2. Матриця других похідних має вигляд:
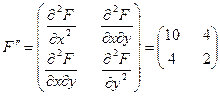
3. Перевіримо кутові мінори: 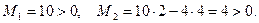
4. По критерію Сильвестра матриця додатньо визначена, тоді 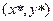 - точка строгого локального мінімуму. Вона буде також точкою строгого глобального мінімуму, оскільки функція F(x,y) нескінченно зростаюча на
- точка строгого локального мінімуму. Вона буде також точкою строгого глобального мінімуму, оскільки функція F(x,y) нескінченно зростаюча на 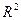 .
.
5. F 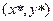 =-52.
=-52.
Приклад 6.2. 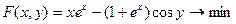
Розв’язок:
Знайдемо стаціонарні точки:
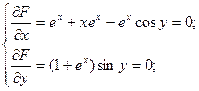
Розв`яжемо систему:
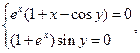
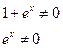
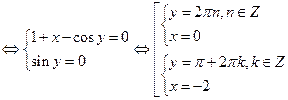
Отже, точками, які задовольняють системі рівнянь, будуть
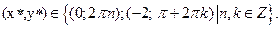
Матриця других похідних має вигляд:
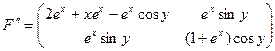
Дослідимо першу групу точок:
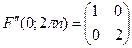
Перевіримо кутові мінори: М1=1>0, M2=1∙2-0∙0>0. По критерію Сильвестра отримуємо, що матриця других похідних в точці 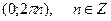 , додатньо визначена. Отже, в цій точці маємо строгий локальний мінімум. Знайдемо значення функції F(x,y) в точці
, додатньо визначена. Отже, в цій точці маємо строгий локальний мінімум. Знайдемо значення функції F(x,y) в точці 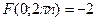 . Ця точка буде точкою глобального мінімуму задачі, оскільки
. Ця точка буде точкою глобального мінімуму задачі, оскільки
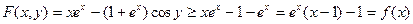
Дослідимо останню функцію однієї змінної на екстремум:
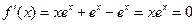 , отже, оскільки
, отже, оскільки 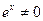 , то
, то 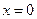 - точка її екстремуму. Значення функції
- точка її екстремуму. Значення функції 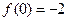 . Це точка мінімуму
. Це точка мінімуму 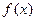 , так як
, так як 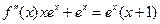 і
і 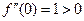 .
.
Дослідимо другу групу точок:
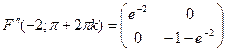
Перевіримо кутові мінори М1= e-2>0, М2= -e-2 (1+e-2)<0. Отже, матриця других похідних в цій точці знаконевизначена. Тому точка 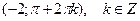 не є точкою екстремуму.
не є точкою екстремуму.
6.2. Задача планування випуску продукції
Для виготовлення виробів X, Y, Z (рис. 6.3) використовують 3 види сировини: I, II, III. У таблиці задано: норми витрат сировини на 1 виріб продукції кожного виду, ціна одного виробу, а також кількість сировини кожного виду, які можна використати. Скільки виробів кожного виду потрібно виготовити, щоб прибуток був максимальний?
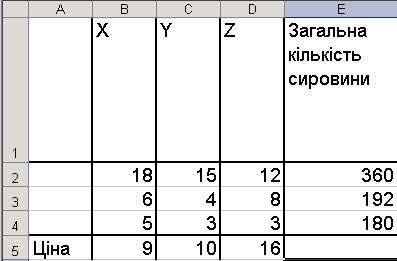
Рис. 6.3
Це задача лінійного програмування і розв’язується за допомогою команди меню Сервис-Поиск решения (рис.6.4). Пошук рішення – це потужний засіб, що дозволяє в загальному випадку розв’язувати задачі як лінійного так і нелінійного програмування.
Математична модель задачі. Треба позначити черезX, Y, Z шукані кількості виробів трьох видів. Знайти X, Y, Z, для яких досягається максимум функції прибутку F=9X+10Y+16Z за таких обмежень:
18X+15y+12Z £360
6X+4Y+8Z £192
5X+3Y+3Z £180
X ³ 0, Y ³ 0, Z ³ 0.
Розв’язок:
1. Треба клітинам A1, B1, C1, D1 присвоїти імена X, Y, Z, F за допомогою команди меню Вставка- Имя-Присвоить.
2. У клітину D1 ввести формулу =9*X+10*Y+16*Z.
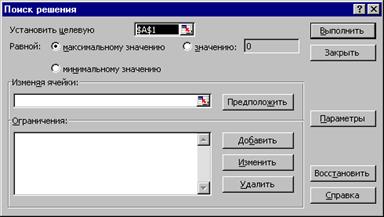 |
Рис. 6.4
3. Викликати команду меню Сервис-Поиск решения.
4. У діалоговому вікні Поиск решений:
а) в полі Установить целевую ячейку задати адресу цільової клітини $D$1.
б) встановити перемикач Равной максимальному значению;
в) в полі Изменяя ячейки вказати імена змінних X;Y;Z;
г) за допомогою кнопки Добавить у діалоговому вікні Параметры поиска решения ввести обмеження у вигляді нерівностей:
X<=(360-15*y-12*z)/18, Y<=(192-6*x-8*z)/4, Z<=(180-5*x-3*y)/5,
x>=0, y>=0, z>=0
Після введення кожної нерівності – клацнути на кнопці Добавить (рис.
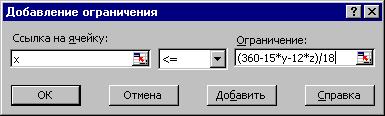 |
6.5, 6.6), а потім – на кнопці ОК.
Рис. 6.5
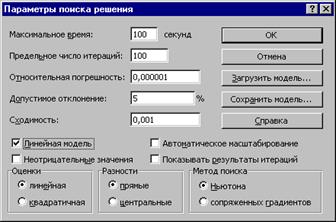 |
Рис. 6.6.
д) натиснути на кнопці Параметр і у діалоговому вікні Параметры поиска решения вказати, що модель є Линейной, після чого клацнути на кнопці ОК.
є) у діалоговому вікні Поиск решений натиснути на кнопці Выполнить, після чого у клітинах A1:D1 висвічуються результати:
X=0; Y=8; Z=20; F=400
5. У діалоговому вікні Результаты поиска решения треба вибрати параметр Сохранить найденное решение.
6.3. Метод повного перебору (метод сіток)
Ідея метода полягає в тому, що допустиму область задачі нелінійного програмування розбивають площинами 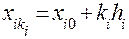 (
(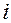 - номер змінної, ki - номер площини, hi - крок), перпендикулярними висям координат, на ряд підобластей. На перетині цих площин в області допустимих значень отримуємо точки
- номер змінної, ki - номер площини, hi - крок), перпендикулярними висям координат, на ряд підобластей. На перетині цих площин в області допустимих значень отримуємо точки 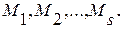 В кожній з них обчислюємо значення цільової функції f(X) і отримуємо множину значень
В кожній з них обчислюємо значення цільової функції f(X) і отримуємо множину значень 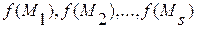 . З цієї множини значень вибираємо максимальне значення, якщо задача розв’язується на максимум цільової функції або мінімальне значення, якщо задача розв’язується на мінімум. Точка Mr, яка відповідає екстремальному значенню функції f(X) і вважається розв’язком задачі. Слід відмітити, що чим менше крок hi, тим більше треба будувати площин і обчислювати точок Ms і тим точніше розв’язується задача. Але, чим більше точок Ms, тим більше обчислень треба провести, а чим більше змінних, тим більше точок Ms. Тому такий метод найчастіше використовується для задач з двома змінними.
. З цієї множини значень вибираємо максимальне значення, якщо задача розв’язується на максимум цільової функції або мінімальне значення, якщо задача розв’язується на мінімум. Точка Mr, яка відповідає екстремальному значенню функції f(X) і вважається розв’язком задачі. Слід відмітити, що чим менше крок hi, тим більше треба будувати площин і обчислювати точок Ms і тим точніше розв’язується задача. Але, чим більше точок Ms, тим більше обчислень треба провести, а чим більше змінних, тим більше точок Ms. Тому такий метод найчастіше використовується для задач з двома змінними.
Приклад.Знайти максимум функції
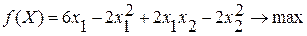
при обмеженнях
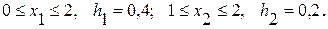
Розв’язання. У даному прикладі x10=0, x20=1. Оберемо крок h1=0,4 та h2=0,2. Відрізок [0, 2] для змінної 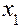 розбиваємо на 6 частин:
розбиваємо на 6 частин:
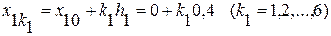 .
.
Відрізок [1, 2] змінної x2 поділимо теж на 6 частин:
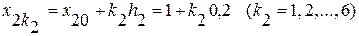 .
.
Для кожної пари значень 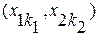 отримуємо точку. Оскільки k1 і k2 приймають 6 значень, то кількість всіх точок складає 36.
отримуємо точку. Оскільки k1 і k2 приймають 6 значень, то кількість всіх точок складає 36.
Визначимо максимальне значення функції f(X)=6 при x1=2,0 і x2=1,0, що і є рішенням задачі.
 2015-05-20
2015-05-20 222
222







