Как составляются узловые и контурные уравнения для электрической сети?

Ответ: Узловые уравнения могут быть записаны через матрицу узловых Проводимостей 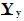и матрицу узловых сопротивлений Z: 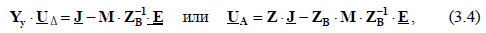где 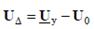столбец разностей напряжений U_y в n-1 узлах по отношению к напряжению базисного узла 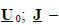столбец узловых токов; E - столбец ЭДС в ветвях; 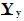- – квадратная матрица узловых проводимостей. По главной диагонали матрицы 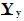находятся элементы 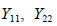и т. д., представляющие собой собственные проводимости узла или сумму проводимостей всех ветвей, связанных с данным узлом. Остальные элементы этой матрицы представляют собой проводимости ветвей между соответствующими узлами, взятые с обратными знаками. Напряжения в узлах и токи в ветвях определяются при отсутствии ЭДС в ветвях и несовпадении балансирующего и базисного узлов: 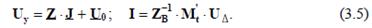Здесь 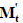– транспонированная матрица 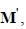представляющая собой первую матрицу соединений, но записанная для того случая, когда

базисный и балансирующий узлы в схеме замещения не совпадают. Отличие состоит в том, что в матрице М отсутствует строка, отвечающая балансирующему (совпадающему с базисным) узлу, а в матрице 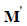отсутствует строка, отвечающая базисному узлу. Если базисный и балансирующий узлы совпадают, то вместо 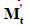употребляется матрица 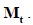Контурные уравнения, по которым вычисляются токи в ветвях, имеют вид: 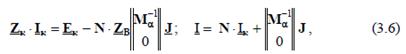где 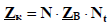– квадратная матрица контурных сопротивлений; 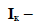матрица контурных токов; I - столбец токов в ветвях; 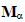– подматрица первой матрицы соединений М, характеризующая связь ветвей де-

рева с ее узлами: где 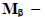также подматрица матрицы М, показывающая связь между хордами схемы и ее узлами. При составлении матрицы М сначала записываются столбцы, отвечающие ветвям, образующим дерево схемы, а затем ветвям, являющимися ее хордами.