Основные понятия: порядок элемента группы, циклическая группа; описание подгрупп циклической группы.
Задание 1. Найти порядок элементов 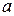 или b данной группы:
или b данной группы:
1) 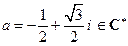 ;
; 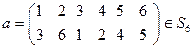 ;
; 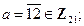
2) 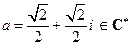 ;
; 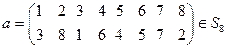 ;
; 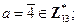
3) 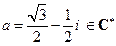 ;
; 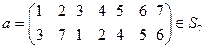 ;
; 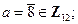
4) 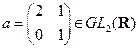 ;
; 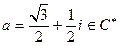 ;
; 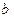 - поворот на
- поворот на 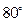 в группе D18;
в группе D18;
5) 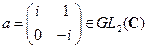 ;
; 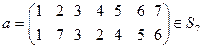 ;
; 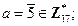
6) 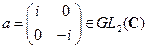 ;
; 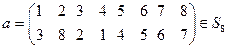 ;
; 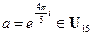 ;
;
7) 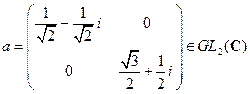 ;
; 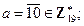
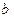 - поворот на
- поворот на 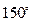 в группе D12;
в группе D12;
8) 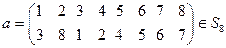 ;
; 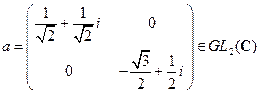 ;
; 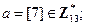
9) 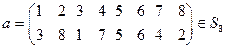 ;
; 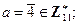
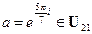 ;
;
10) 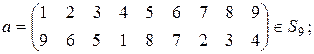
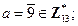
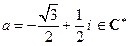
11) 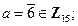
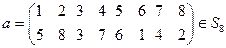 ;
; 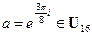 ;
;
12) 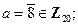
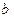 - поворот на
- поворот на 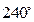 в группе D15;
в группе D15; 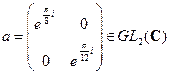 .
.
Задание 2. Найти порядок элемента 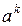 , если порядок
, если порядок 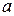 равен
равен 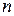 :
:
1) 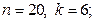 2)
2) 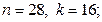 3)
3) 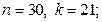
4) 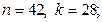 5)
5) 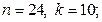 6)
6) 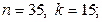
7) 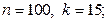 8)
8) 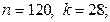 9)
9) 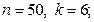
10) 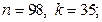 11)
11) 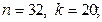 12)
12) 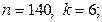
Задание 3. Найти все подгруппы циклической группы порядка:
1) 36; 2) 54; 3) 28; 4) 98; 5) 120; 6) 48; 7) 52; 8) 64; 9) 200; 10) 96; 11) 150; 12) 132.
Задание 4.
- Доказать, что пересечение двух подгрупп является подгруппой.
- Доказать, что во всякой группе элементы ху и ух имеют один и тот же порядок.
- Доказать, что во всякой группе элементы х и уху-1 имеют один и тот же порядок.
- Доказать, что во всякой группе четного порядка имеется элемент порядка 2.
- Доказать, что группа, в которой все элементы имеют порядок 2, коммутативна.
- Доказать, что периодическая часть коммутативной группы является подгруппой.
- Доказать, что в коммутативной группе множество элементов, порядки которых делят фиксированное число n, является подгруппой. Верно ли это утверждение для некоммутативной группы?
- Доказать, что объединение двух подгрупп является подгруппой тогда и только тогда, когда одна из подгрупп содержится в другой.
- Доказать, что если подгруппа С содержится в объединении подгрупп А и В, то либо С содержится в А, либо С содержится в В.
- Пусть элементы х и у группы G имеют конечный порядок и ху = ух. Доказать, что если порядки элементов х и у взаимно просты, то порядок произведения ху равен произведению их порядков.
- Пусть элементы х и у группы G имеют конечный порядок, и ху = ух. Найти порядок элемента х у.
- Доказать, что если в коммутативной группе G есть элементы бесконечного порядка, и все они содержатся в подгруппе H, то H совпадает с G.
 2015-05-10
2015-05-10 2992
2992