Свойства группы

1. В группе определено произведение любого конечного числа элементов.

2. Существует единственный единичный элемент 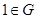такой, что , .

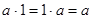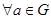3. 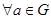существует единственный обратный элемент 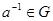такой, что .

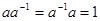4. .

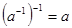5. .

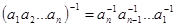Теорема 9.1: Множество 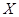с ассоциативной операцией (умножение) является группой, если существует 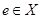такой, что 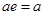, , 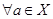среди элементов 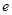существует такой, что 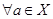существует 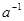такой, что .

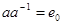Определение 9.4: Группы 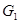и 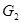называются изоморфными, если существует взаимнооднозначное отображение 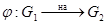такое, что .

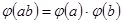Определение 9.5: 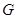– группа. Множество 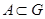называется подгруппой группы 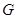, если является группой относительно операции, введенной в .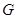

В группе вводится степень элемента 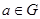: 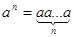, 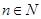. 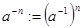, 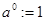– единица группы.

Теорема 9.2: – подгруппа 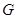, если:

1. 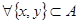, 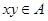и .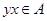

2. , .

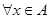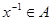Теорема 9.3: Есл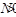и и 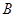– подгруппы группы 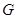, то 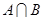– подгруппа .

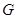Определение 9.6: Подгруппа 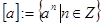называется циклической подгруппой, – образующий элемент.

Определение 9.7: Пусть существует положительное число такое, что

1. .

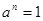2. Если 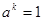, , 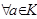то .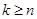

Тогда говорят, что есть элемент конечного порядка .

Теорема 9.4: Если порядок элемента равен , то .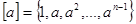

Следствие: Если элемент имеет конечный порядок , то его циклическая подгруппа имеет тоже порядок .

Определение 9.8: Если циклическая подгруппа 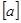состоит из бесконечного числа элементов, то элемент называется элементом бесконечного порядка.

Определение 9.9: Группа 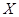называется циклической, если существует 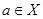такой, что 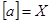, называется образующим элементом группы .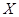

Теорема 9.5: Все бесконечные циклические группы изоморфны между собой. Все конечные циклические группы порядка изоморфны между собой.

Теорема 9.6: Всякая подгруппа циклической группы является циклической.