Экспериментальная установка
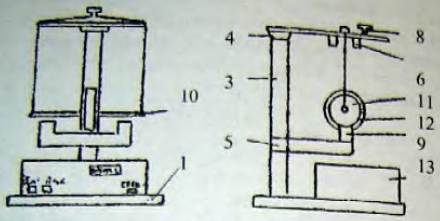 1 – основание, 3 – колонка, 4 – неподвижный верхний кронштейн, 5 – подвижный нижный кронштейн,
1 – основание, 3 – колонка, 4 – неподвижный верхний кронштейн, 5 – подвижный нижный кронштейн,
6 – электромагнит, 7 – груз крестовины, 8 – фотоэлектрический датчик, 9 –фотоэлектрический датчик, 10 – ось, 11 – диск,
12 – сменные кольца, 13 – электронный секундомер.
Цель работы: Изучение движения маятника Максвелла и проверка закона сохранения механической энергии.
- Надеваем на диск маятника сменное кольцо массой 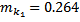 кг;
кг;
- Затем на ось маятника равномерно виток к витку наматываем нить подвески, фиксируем маятник с помощью электромагнита так, чтобы нить не была слишком натянута;
- Нижимаем клавишу «Пуск», измеряем значение времени t падения маятника;
- Повторим измерения для сменного кольца массой 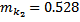 кг;
кг;
- Заполняем Таблицу 1, повторив 5 раз;
Таблица 1
| m, кг | t1, c | t2, с | t3, с | t4, с | t5, с | 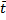 , с , с
|
| 0,264 | 1,88 | 1,85 | 1,87 | 1,88 | 1,89 | 1,87 |
| 0,528 | 2,05 | 2,08 | 2,06 | 2,04 | 2,08 | 2,06 |
- Используя измеренные значения t, по формуле 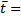
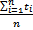 вычислим среднее значение времени t движения каретки 12 до нижнего уровня;
вычислим среднее значение времени t движения каретки 12 до нижнего уровня;
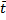 для m=0,264 кг.
для m=0,264 кг. 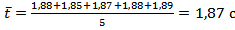 .
.
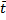 для m=0,528 кг.
для m=0,528 кг. 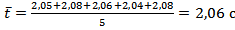 .
.
- Определим момент инерции по формуле 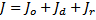 , где
, где 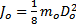 – момент инерции оси маятника (
– момент инерции оси маятника (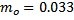 кг – масса оси маятника,
кг – масса оси маятника, 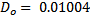 м – диаметр оси маятника),
м – диаметр оси маятника),
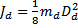 – момент инерции диска (
– момент инерции диска (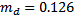 кг – масса диска маятника,
кг – масса диска маятника, 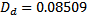 м – диаметр диска маятника),
м – диаметр диска маятника), 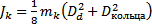 – момент инерции кольца (
– момент инерции кольца (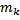 – масса сменного кольца,
– масса сменного кольца, 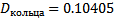 м – внешний диаметр диска):
м – внешний диаметр диска):
для 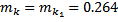 кг:
кг:

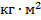
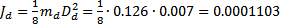
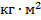
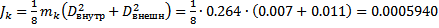
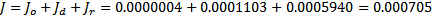
- для 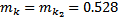 кг:
кг:

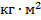
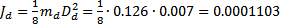
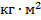
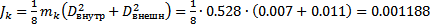
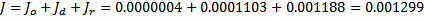
- Проверим закон сохранения механической энергии проверкой справедливости равенства:
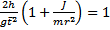 , где h = 0.27 м, g = 9.8
, где h = 0.27 м, g = 9.8 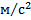 ,
, 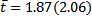 c,
c, 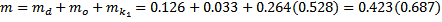 кг.,
кг., 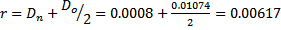 м.:
м.:
для 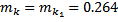 кг:
кг:
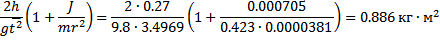
для 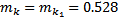 кг:
кг:
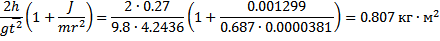
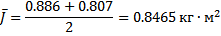
- Воспользуемся методом Стьюдента и рассчитаем абсолютную погрешность измерений момента инерции 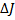 по формуле:
по формуле:
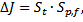
где 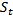 – среднеквадратичная погрешность и определяется как
– среднеквадратичная погрешность и определяется как
 - коэффициент Стьюдента
- коэффициент Стьюдента
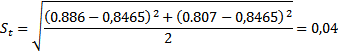
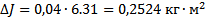
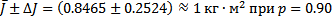
- Подсчитав число подъёмов (колебаний маятника) 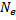 при уменьшении высоты подъёма в e = 2.7 раз, найдём логарифмический декремент затухания колебаний маятника
при уменьшении высоты подъёма в e = 2.7 раз, найдём логарифмический декремент затухания колебаний маятника 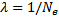 и его добротность
и его добротность 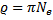 :
:
для 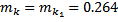 кг,
кг, 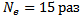 :
:
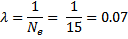
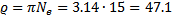
для 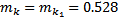 кг,
кг, 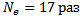 :
:
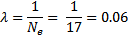
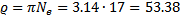
 2015-05-10
2015-05-10 236
236






