Теоретические введение

Ивановский государственный энергетический университет имени В.И. Ленина

Кафердра прикладной математики

Отчет по лабораторной работе №1

Тема: математический аппарат, знакомство с пакетом Mat lab, табулирование функций, построение графиков функций.

Выполнил

студент 1 курса 36 группы

Кравале Илья

Проверил доцент

кафедры прикладной математики

Митрофанов А. В.

Цель работы: ознакомиться с пакетом Mat lab.Научиться владеть оперциями ввода-вывода данных, научиться графически их представлять.

Теоретические введение.

Данная лабораторная работа является ознакомительной. Мы познакомились с пакетом Mat lab, а также насколько он облегчает особо сложные вычисления. Mat lab переводится, как «матричная лаборатория». Все мы знаем насколько сложные операции встречаются при работе с матрицами. С ними и поработаем. И так, что такое матрица?

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. С курсов математики знаем, что матрицы можно:

1) Складывать

2) Вычитать

3) Умножать

4) Транспонировать

Складывать и вычитать матрицы можно лишь одинаковые, т.е. имеющие одинаковое количество столбцов и строк. Математический аппарат умножения матриц уже чуть сложней. Пусть даны две прямоугольные матрицы 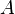и 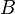размерности m × n и n × q соответственно:

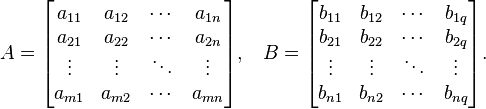
Тогда матрица 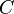размерностью 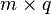называется их произведением:

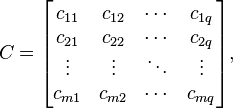
где:

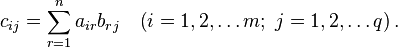
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Следует заметить, что из существования произведения 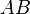вовсе не следует существование произведения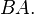

Но иногда требуется матрицу разделить на другую матрицу. Что делать в таком случае? Вспомним элементарную математику. Допустим требуется 20 поделить на 10. Преобразуем эту операцию в умножение и получим 20× 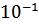. Также и в матрицах. Если требуется матрицу А поделить на матрицу В, то матрицу А умножают на 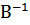. 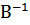- называют обратной матрицей. Одно из свойств обратной матрицы, что при умножении ее на исходную, получается единичная матрица, т.е. матрица, у которой на главной диагонали располагаются единицы, а все остальные элементы – нули.

Как найти обратную матрицу? Во первых требуется проверить ее существование, т.е. найти определитель(детерминант). Детерминант существует только для квадратных матриц n×n, и в данном контексте, он не должен быть равен нулю. В общем для матрицы первого порядка значение детерминанта равно единственному элементу этой матрицы:

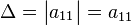
Для матрицы 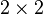детерминант вычисляется как

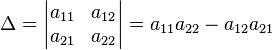
В частности, формула вычисления определителя матрицы 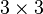такова:

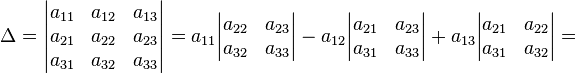
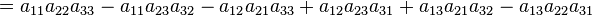
Теперь, когда проверили существование обратной матрици, т.е., допустим, определитель не равен нулю, можно заняться ее поиском. Формула такова:

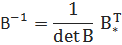
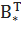- транспонированное алгебраическое дополнение, которое по своей сути есть матрица таких же размеров как и В. Алгебраическим дополнением элемента 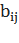матрицы B называется число

,

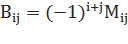где 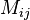— дополнительный минор, определитель матрицы, получающейся из исходной матрицы B путем вычёркивания i -й строки и j -го столбца. Использовали еще одну операцию, которую не описали – транспонирование. Транспонирование матрицы – замена столбцов на строки.

Табулирование функции — это вычисление значений функции при изменении аргумента от некоторого начального значения до некоторого конечного значения с определённым шагом. Именно так составляются таблицы значений функций, отсюда и название — табулирование. Необходимость в табулировании возникает при решении достаточно широкого круга задач. С помощью табулирования можно найти минимум или максимум функции. Иногда случается так, что функция не имеет аналитического представления, а её значения получаются в результате вычислений, что часто бывает при компьютерном моделировании различных процессов.