Построить график функции:
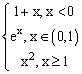 |
При построении этого графика следует использовать функцию ЕСЛИ. Например, в ячейке А7 (см. рис. 4.3) находится начальное значение аргумента, тогда в ячейку В7 необходимо ввести формулу:
=ЕСЛИ(A7<0;1+A7;ЕСЛИ(A7>=1;A7^2;EXP(A7))).
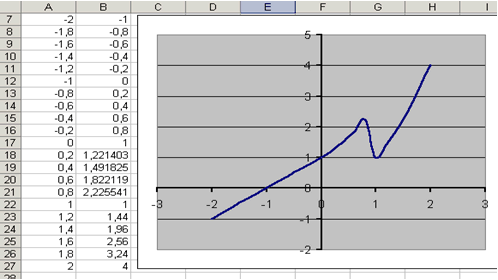 |
| Рис. 4.3 |
ПРИМЕР 4.5. Изобразите линию, заданную неявно уравнением:
| 4 y 2 +5 x 2 - 20=0. |
Заметим, что заданная уравнением f(x,y)=0 функция описывает кривую линию под названием эллипс. Это можно доказать, если произвести элементарные математические операции:
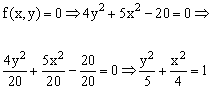 |
В связи с тем, что линия задана неявно, для ее построения необходимо разрешить заданное уравнение относительно переменной y:
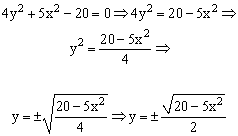 |
После проведенных преобразований можно увидеть, что линию f(x,y) можно изобразить, построив графики двух функций в одной графической области.
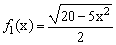 | и | 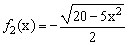 |
Перед построением определим ОДЗ функций f 1 (x) и f 2 (x).
Поскольку эти функции содержат в числителе выражение под знаком квадратного корня, то обязательным условием их существования будет выполнение следующего неравенства:
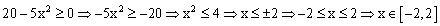 |
Теперь перейдем к построению графика.
Для этого в диапазон А3:А43 введем значения аргумента (от -2 до 2 с шагом 0,1).
В ячейку В3 введем формулу для вычисления значений функции f 1 (x):
=КОРЕНЬ(20-5*$A3^2)/2.
А в ячейку С3 для вычисления значений функции f 2 (x):
= - КОРЕНЬ(20-5*$A3^2)/2.
Далее скопируем эти формулы до В43 и С43 соответственно (см. рис. 4.4).
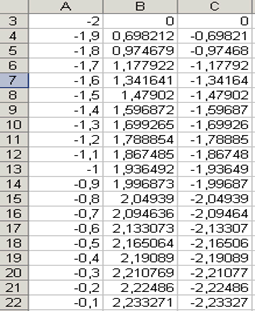 | 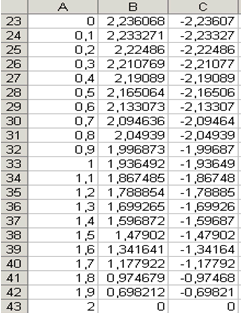 | |
| Рис. 4.4 |
Затем выделим диапазон А3:С43 и воспользовавшись "Мастером диаграмм", построим графики функций f 1 (x) и f 2 (x) в одной графической области (см. рис. 4.5).
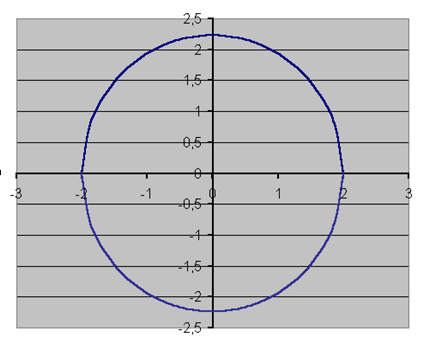 |
| Рис. 4.5 |
ПРИМЕР 4.6. Изобразите линию заданную неявно:
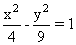 |
Данное уравнение описывает линию под названием гипербола. Разрешим его относительно переменной y:
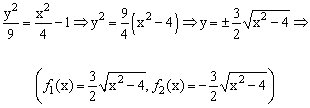 |
| Найдем ОДЗ функций f 1 (x) и f 2 (x): | 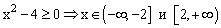 |
Проведенные исследования показывают, что для построения графика необходимо значения аргумента задавать в два этапа, т.к. в диапазоне от -2 до 2 функция не определена (см. ПРИМЕР 4.2 и 4.3).
Задание значений функций f 1 (x), f 2 (x) и построение графика выполняется так же, как в ПРИМЕРЕ 4.5. Результаты представлены на рис. 4.6. и 4.7.
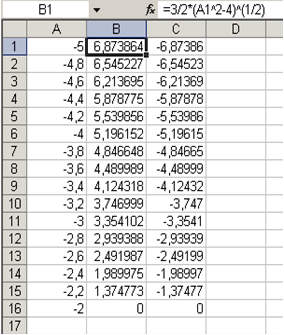 | 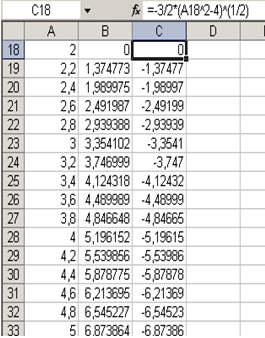 | |
| Рис. 4.4 |
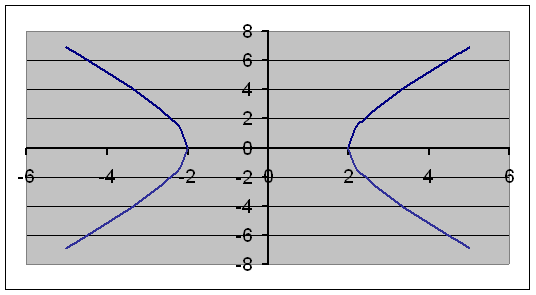 |
ВАРИАНТЫ ЗАДАНИЙ
ЗАДАНИЕ 4.1. Построить график функции f(x).
| № | f(x) | № | f(x) | № | f(x) |
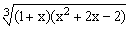 | 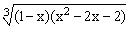 | 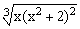 | |||
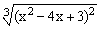 | 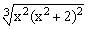 | 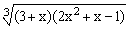 | |||
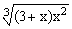 | 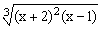 | 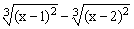 | |||
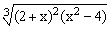 | 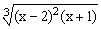 | 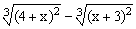 | |||
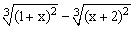 | 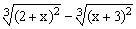 | 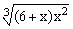 | |||
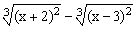 | 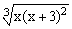 | 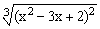 | |||
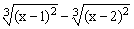 | 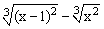 | 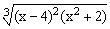 | |||
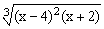 | 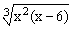 | 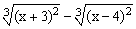 | |||
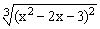 | 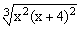 | 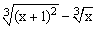 | |||
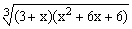 | 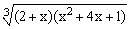 | 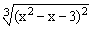 |
ЗАДАНИЕ 4.2. Построить график функции f(x).
| № | f(x) | № | f(x) | № | f(x) |
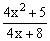 | 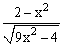 | 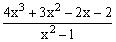 | |||
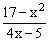 | 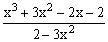 | 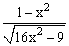 | |||
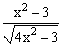 | 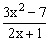 | 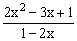 | |||
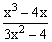 | 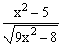 | 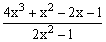 | |||
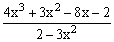 | 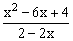 | 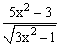 | |||
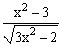 | 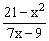 | 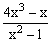 | |||
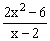 | 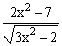 | 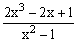 | |||
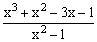 | 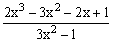 | 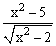 | |||
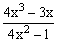 | 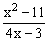 | 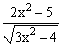 | |||
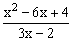 | 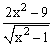 | 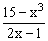 |
ЗАДАНИЕ 4.3. Построить график функции f(x).
| № | f(x) | № | f(x) | № | f(x) |
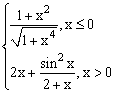 | 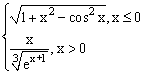 | 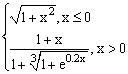 | |||
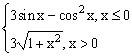 | 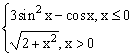 | 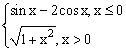 | |||
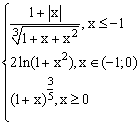 | 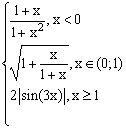 | 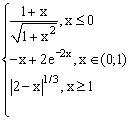 | |||
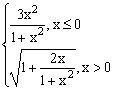 | 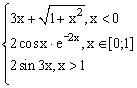 | 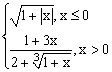 | |||
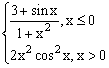 | 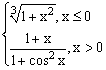 | 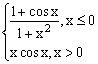 | |||
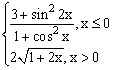 | 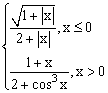 | 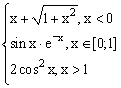 | |||
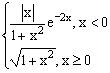 | 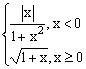 | 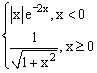 | |||
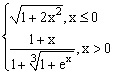 | 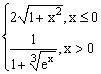 | 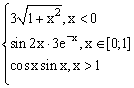 | |||
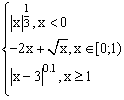 | 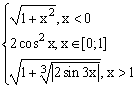 | 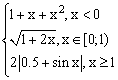 | |||
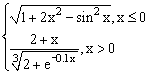 | 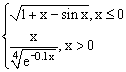 | 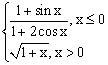 |
ЗАДАНИЕ 4.4. Изобразите линии заданные неявно уравнением f(x,y)=0.
| № | f(x) | № | f(x) | № | f(x) |
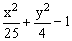 | 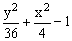 | 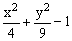 | |||
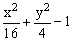 | 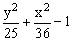 | 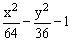 | |||
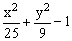 | 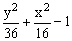 | 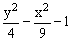 | |||
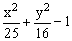 | 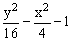 | 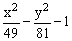 | |||
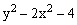 | 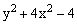 | 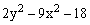 | |||
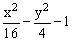 | 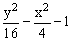 | 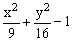 | |||
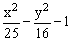 | 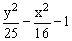 | 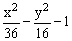 | |||
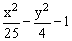 | 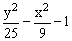 | 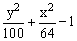 | |||
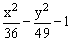 | 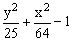 | 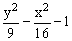 | |||
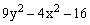 | 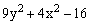 | 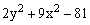 |
 2015-05-10
2015-05-10 1104
1104